Оглавление:




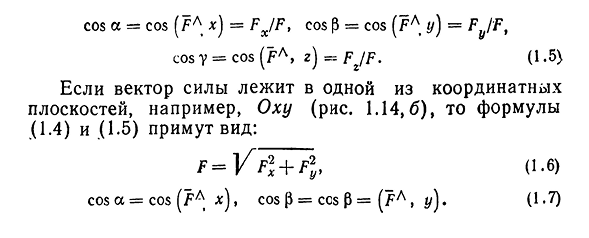

Основные понятия векторной алгебры
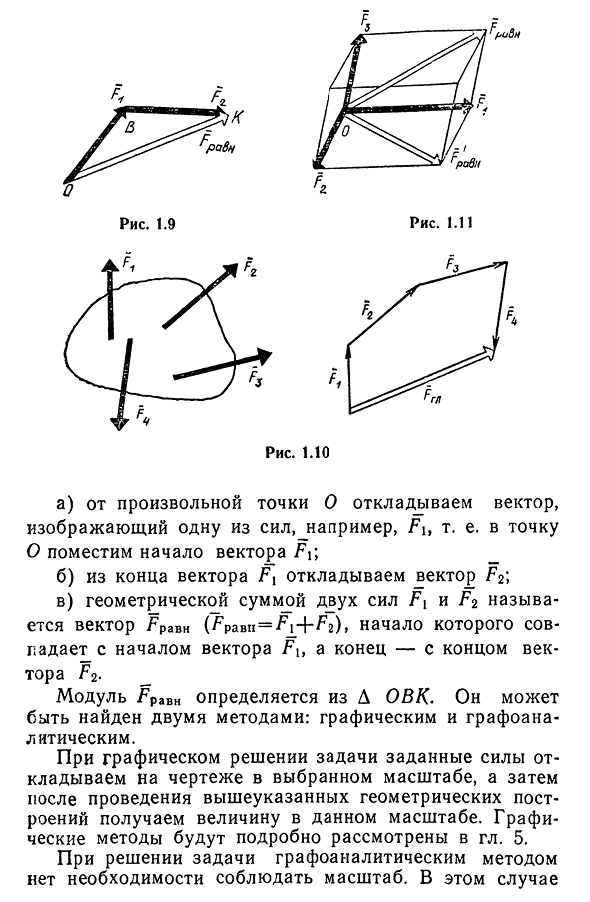
- Основные понятия векторной алгебры _ сложение двух сил . В §1.2 правило параллелограмма нашло геометрическую сумму^, равную двум силам Fi и F2(рис. 1.3). Но правило треугольника(рис.Иногда удобнее использовать другую структуру, называемую). 1.9): 15 лет 1.9 цифры. 1.11 А) из любой точки на векторе задержки, представляющем одну из сил напримера, точка начала L, а именно вектор L;б) из конца вектора F{вектор задержки G2;в) геометрический модуль _ _ FPaBH определяется из D HVAC. Как вы можете найти: графический и
графический анализ. При графическом решении задачи заданная сила переносится на чертеж по выбранному масштабу, затем после приведенной выше геометрической структуры значения получаются по этому масштабу и графический метод подробно описан в главе 5. При решении задач Графоаналитическими методами нет необходимости соблюдать масштаб. В этом деле 16 достаточно знать величину угла между заданными силами, а затем по косинусной теореме Grav = = k f? +G?+ 2G / 2C OS L). (1.1)
Сложение системы сил. Геометрическая сумма ‘ (главный вектор)любой системы Сил Людмила Фирмаль
осуществляется путем непрерывного сложения сил по правилам параллелограмма, или по структуре силовых полигонов и второго способа, более простого и удобного. Таким образом, найти сумму сил Fi, F2i F3f…, FN требуется: а)начало второго вектора F2 В конце первого вектора F, положить начало вектора F3 в конце вектора G2 и т.; б) построить результирующий вектор F2, его начало совпадает с началом вектора f b и концом вектора Fn. Для риса. 1.10 четыре вектора F\t F2l F3, приведен пример составления суммы GGL из F4.
Вектор GGL=F[4-F2+F3+F4 называется замкнутым вектором многоугольника. При построении силового многоугольника необходимо помнить, что во всех терминах вектора стрелка указывает в одном направлении, а замкнутый вектор Frjl-в противоположном. Если силовые линии Fb F2i F3 и G4 пересекаются в некоторой точке, то главный вектор этой системы равен результату, приложенному в точке пересечения. Сложение трех сил, которые не присутствуют в одной плоскости (правило параллелепипеда). Применяя правило параллелограмма по порядку, можно найти
- геометрическую сумму любого числа сил, приложенных к входной точке. Найдем сумму первых трех сил Fb F2, F3, приложенных в точке O и не лежащих на одной плоскости(рис. 1.11). Сложенный по правилам силы F и параллелограмма F2, Получите сумму, которую они выросли’, затем он присоединился к своей силе F3 и вырос , Найти сумму трех заданных сил Fb F2 и F3 FpaBH._Рисунок. Геометрическая сумма трех сил Fif F2 и F3, не лежащих в одной плоскости, представлена диагональю параллелепипеда, построенного на основе этих сил. Расширение сил в двух заданных направлениях. 2-480 17 разложить заданную силу F (рис. 1.12, а) эта сила находится в одной плоскости в направлении, заданном прямой S и OK. Задача
сводится к построению параллелограмма,в котором сила F становится диагональю. Чтобы решить эту проблему, проведите прямую линию через конец силы F, параллельную S и OK. Так как Fx — \ — F2=F, то силы F1 и F2 становятся искомыми компонентами. Его можно разложить на две части.Это позволяет использовать силу треугольника. 1.12, б). Для этого из любой точки 0 отложите силу F, а через ее конец и начало проведите параллельные S и OK прямые к взаимному пересечению. Проекция силы на ось. Проекция силы F для проецирования Fn на ось P.(фиг. (1.13) называется скалярным значением, равным длине отрезка S, и отсекается от оси вертикальной плоскостью, проведенной через начало и конец вектора F.
Другими словами, проекция силы на ось равна ее модулю, умноженному на косинус угла между направлением ее силы и Людмила Фирмаль
положительным направлением оси: / \ npn=f n=f C0S(F ‘ n)-(1 2 ) Если направление равно si, то проекция положительна- 18) положительное направление оси при остром угле, а отрицательное-при тупом.Если >0cos(FA n)>0, то cos(FA, n)=0 равно нулю,а если cos (FA, n)<0-отрицательно. Расширение сил в направлении осей координат. Для того чтобы разложить силу F в направлении трех осей, необходимо построить на этих осях параллелепипед, где вектор F является диагональным(рис. 1.14, а). Проекция вектора F на ось декартовой системы, основанная на Формуле (1.2), имеет следующий вид: Гонка FX=Ф ко СА = Ф cos0 ФГ, ФЗ=Ф уютно. (1.3) Если вы сложите эти выражения в квадрат и сложите их вместе, вы получите
cos2a++cos2p4-cos2y=1 и позже, F2=Fx — ± — Fy -} — Fl. В результате векторный модуль имеет следующую формулу: F=] / f1+F^+F^(1.4) Коэффициент вектора равен квадратному корню из суммы квадратов проекций на любые три взаимно перпендикулярные оси. Косинус угла между вектором и положительным направлением проективной оси называется индуктивным Косинусом. Он равен отношению проекции вектора на соответствующую ось и модулю вектора. Два.* 19cos а=соѕ(Ф А х)=FX с/Ф, cos0 = соѕ(ф г) = ФГ!’F, cos y = cos(? л, з) — диф. (1*5) Если вектор силы находится в одной координатной плоскости, например, OHU(рис. 1.14, 6), формулы (1.4) и (1.5) принимают следующий вид: потому что а=соѕ х), что р=в COS р=, т/). (1.6) (1.7)
Смотрите также:
| Следствия из аксиом | Нормальные напряжения при косом изгибе |
| Виды связей и их реакции | Касательные напряжения при изгибе балки |

