Основные формы дифференциальных уравнений динамики материальной точки

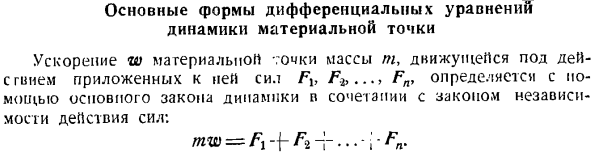
Основные формы дифференциальных уравнений динамики материальной точки

• Основные формы дифференциальных уравнений динамики массовой точки Усилие Fv F2, которое прикладывается к агрегату… Ускорение материальной массы точки m, которая движется под действием Fn, w определяется с помощью закона фундаментальной динамики, который сочетается с законом независимости действия сил. МВт-г. г…- [- Сноска.

Дифференциальное уравнение для движения точки массы в проекции на естественное ПО в декартовых координатах имеет вид: С. С. С. ТХ = ту =£fky по МЗ =>]Гtu\ к-= 1 А — = я Здесь. v, y, z-проекция ускорения w, i l: Ux%i’KV, а также сила Ki Наноинтенсивности на соответствующей оси декартовых координат. Дифференциальное уравнение для движения точки массы в проекции на ось естественного трехгранного тела описывается в следующем виде: Ф! В. х г в-г г С \ В С — ft = 2> » y = V 0 = 2 Красный> V здесь.

Проекционное направление касательной скорости локуса, v-модуль скорости, Людмила Фирмаль

[>- радиус кривизны этого локуса До точки f * l_, f * » i,/-’^ — проекция силы Z7 на ось естественного трехплоскостного тела (m-касательная, n-главная линия закона, b-бинормальная). Проекция результирующей силы, приложенной к материальной точке, на бинормальную равна нулю, как следует из последнего выражения: то есть орбита устроена таким образом, что полученный сплав представляет собой лежащую контактную поверхность, которая притягивается к определенной точке орбиты.

ИД дифференциального уравнения для плоского движения точки масс и полярных координат равен: н Т {? — Р $»)= \ ФКР(РП)= в в / Яk? Я… Где r-радиус-вектор точки, а < p-полярный угол (рисунок PO). Дифференциальное движение точек масс записывается в соответствии с выбранной системой координат. Поэтому dns {> FS-репниальный Уран может быть размещен в цилиндрических координатах, сферических координатах и других криволинейных coordinates.

• In глава X§ II ниже приводится дифференциальное уравнение движения точек масс, которое присваивается любой системе координат. Рисунок 110. Можно решить 2 основные задачи динамики с помощью дифференциального уравнения движения массы point.

It это прямая проблема и обратная проблема. Первична задача, и результирующая сила, приложенная к этой точке, определяется массой данного движения и материальной точки.

Следующий абзац будет посвящен решению прямой задачи динамики важных моментов. Людмила Фирмаль

Эта задача называется обратной задачей, когда задается сила и масса материальной точки, определяется ее движение.

Смотрите также:

Предмет теоретическая механика

Общий случай движения твердого тела. Сложение поступательных и вращательных движений	Определение сил по заданному движению
Динамика	Определение движения по заданным силам