Оглавление:
Основное уравнение динамики для относительного движения материальной точки
Основное уравнение динамики точки верно лишь по отношению к абсолютному движению точки, т. е. к ее движению относительно инерциальной системы отсчета.
Пусть требуется по заданным силам, действующим на материальную точку, определить ее относительное движение, т.е. движение точки по отношению к системе отсчета, которая сама совершает произвольное, но известное нам движение относительно инерциальной системы отсчета. Для решения этой задачи можно было бы поступить следующим образом: по заданным силам, действующим на данную материальную точку, определить сначала ее абсолютное движение, т. е. решить вторую задачу динамики, а затем, зная абсолютное и переносное движения точки, определить, по установленным в кинематике правилам, искомое относительное движение точки.
Существует, однако, формальный прием, позволяющий данную задачу решить значительно проще.
Согласно основному уравнению динамики для абсолютного движения точки имеем:
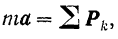
где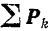 
— геометрическая сумма всех приложенных к точке сил, в том числе и реакций связен.
Из кинематики (§ 57) известно, что при произвольном переносном движении абсолютное ускорение 
точки равно геометрической сумме трех ускорений: переносного 
, относительного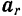 
и кориолисового 
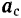, т.е.
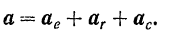
Подставляя это выражение абсолютного ускорения в основное уравнение динамики, будем иметь:
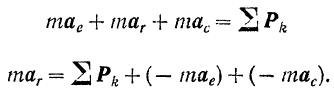
Стоящие в правой части последнего уравнения векторы —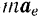
и —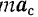
имеют, очевидно, размерности сил. Обозначим их соответственно через 
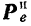и 
.
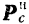Вектор 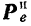, равный произведению массы m точки на се переносное ас ускорение и направленный в сторону, противоположную этому ускорению, называется переносной силой инерции.
Вектор 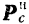, равный произведению массы m точки на ее кориолисово 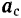ускорение и направленный в сторону, противоположную этому ускорению, называется кориолисовой силой инерции.
Подставив обозначения этих векторов в уравнение (II), получим:
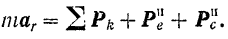
Присоединение к активным силам и реакциям свя-I!сii переносной и кориолисовой сил инерции учитывает влияние перемещения подвижной системы отсчета на относительное движение точки.
Рассмотрим некоторые частные случаи.
- Подвижная система отсчета движется поступательно. прямолинейно и равномерно.
В этом случае
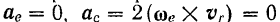
и потому переносная 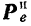и кориолнсова 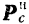силы инерции точки также равны нулю. Следовательно, уравнение (113) относительного движения точки в данном случае ничем не отличается от уравнения (106) ее абсолютного движения.
Такая система отсчета является, как об этом уже было сказано выше (стр. 236), инерциальной.
Связь между силами, действующими на точку, и ее движением по отношению к такой системе отсчета не зависит от того, находится ли эта система в покос по отношению к «неподвижной» или движется относительно нее поступательно, прямолинейно и равномерно.
Отсюда вытекает установленный еще Галилеем принцип относительности классической механики:
никакие механические явления не могут обнаружить, находится ли данная система в покое или движется поступательно, прямолинейно и равномерно.
- Точка находится в положении относительного равновесия. т. е. не совершает движения относительно подвижной системы отсчета.
В этом случае
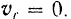
Следовательно, равны нулю кориолисово ускорение точки
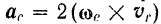
и кориолисова сила инерции
Равно нулю также и относительное ускорение точки
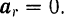
Таким образом, в случае относительного равновесия точки уравнение (113) принимает вид
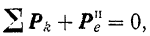
т.е. должна равняться нулю геометрическая сумма: сил, действующих на нее со стороны других тел, и ее переносной силы инерции.
Пример задачи:
Тело массы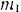 
может скользить без трения по наклонной плоскости (рис. 170), составляющей с горизонтом угол 
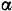. Наклонная плоскость массы 
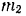лежит на катках и может перемещаться (без трения) по горизонтальной плоскости. С какой горизонтальной силой 
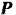надо двигать наклонную плоскость, для того чтобы лежащее на ней тело оставалось относительно этой плоскости в покое. Определить также силу давления тела на наклонную плоскость.
Решение:
Рассматриваем поступательно движущееся тело как материальную точку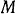 
. Из условия (114) относительного равновесия этой точки найдем, при каком переносном ускорении 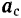этой точки (т. е. ускорении наклонной плоскости) она будет оставаться в положении равновесия относительно наклонной плоскости.
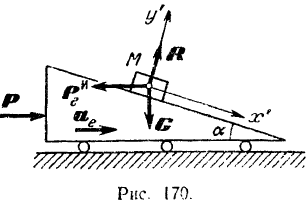
На точку 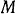действуют силы: 
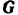— ее сила тяжести и 
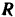— нормальная реакция плоскости. Приложим к точке ее переносную 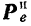силу инерции, равную по модулю 
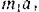, и направленную в сторону, противоположную переносному ускорению.
Связав с движущимся телом координатные ос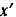и 
и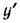 
так, как показано на рис. 170. и проектируя на них силы 
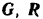и 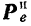будем иметь:
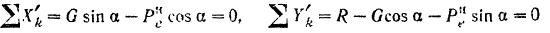
или. подставляя в эти уравнения значения
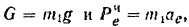
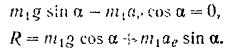
Из уравнения (1) определяем переносное ускорение
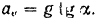
Подставляя это значение в уравнение (II), находим нормальную реакцию плоскости, а следовательно, и силу давления тела на плоскость:
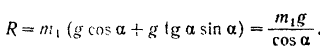
Так как наклонная плоскость вместе с находящимся па ней телом должна двигаться по неподвижной горизонтальной плоскости с ускорение то, при отсутствии сопротивления этому движению, искомая сила
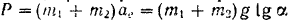
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
