Оглавление:









Осесимметрическое обтекание круглого конуса. Конические течения. Обтекание осесимметричных тел
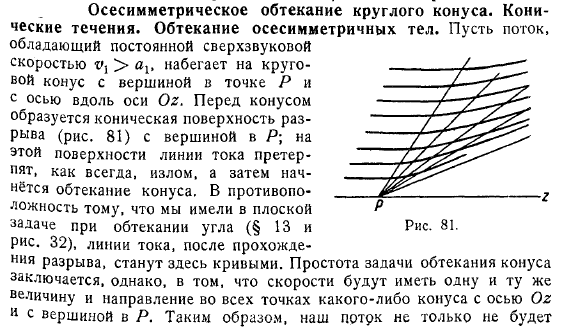
Осесимметрическое обтекание круглого конуса. Конические течения. Обтекание осесимметричных тел. Поток постоянный сверхзвуковой поток, с вершинами в точке p и конусом с осью вдоль оси od. На передней части конуса образуется коническая поверхность излома (рис. 81), а вершина находится на этой поверхности, обтекатель закручивается как обычно, и начинается обтекание конуса. Обтекание после прохождения, в отличие от плоских задач (§ 13 и 32) при обтекании под углом, здесь будет кривая.
Смотрите также:
Простота задачи обтекани заключается, однако, в том. что скорости будут иметь одну и ту же величину и направление во всех точках какого-либо конуса. Людмила Фирмаль
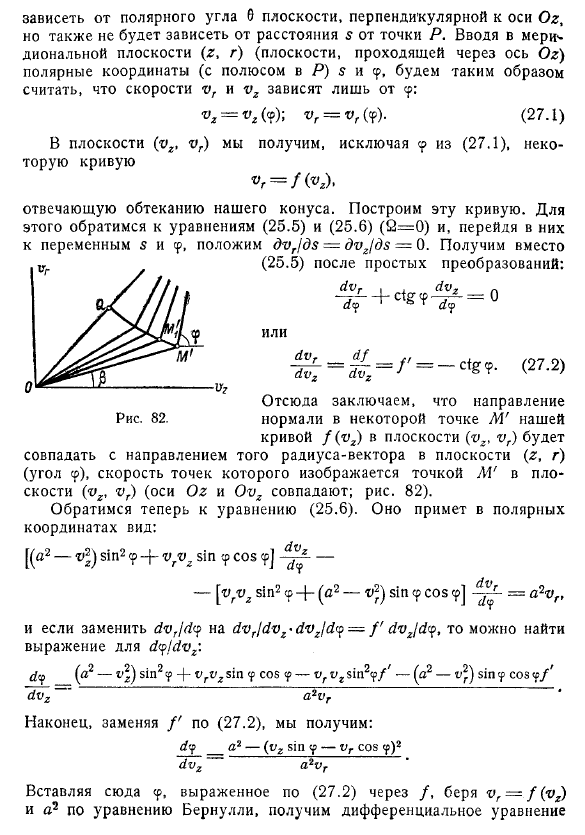
Однако простота потока вокруг k заключается в нем. Скорость имеет одинаковую величину и направление во всех точках конуса с вершинами b и r. Следовательно, она зависит от полярного угла плоскости, перпендикулярной оси og, но также не зависит от расстояния$от точки p. Введите полярные координаты (полюса p) в меридиональной плоскости (r, d) (плоскости, проходящей через ось og) и предположите, что скорости зависят только от g, следовательно, вы получаете некоторые кривые, за исключением 2.
Смотрите также:
Безвихревое осесимметрическое движение при. Метод Франкля.
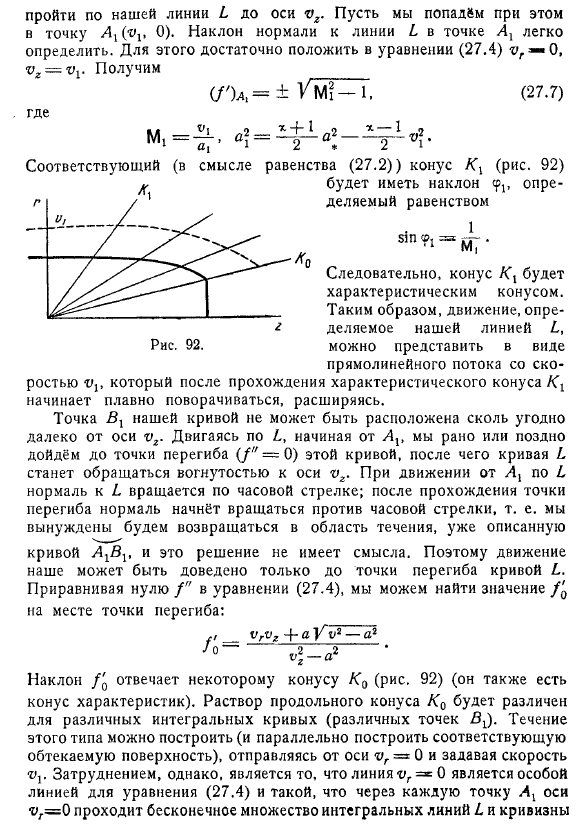
Вы можете сделать следующее (27.4 Предположим, мы знаем, что в какой-то момент m в кривой. То есть для нашего движения мы предполагаем, что мы знаем скорость и величину конкретного конуса, вершины которого являются p (27.2) и (27.3), то вы можете предоставить графический способ аппроксимации состава кривой движения. Если вы знаете bm, вы можете вычислить p из (27.3). Если мы положим p в направлении, нормальном к m (потому что направление известно (потому что p известно), мы найдем центр кривизны и нарисуем небольшую дугу окружности с радиусом p вокруг n.
Смотрите также:
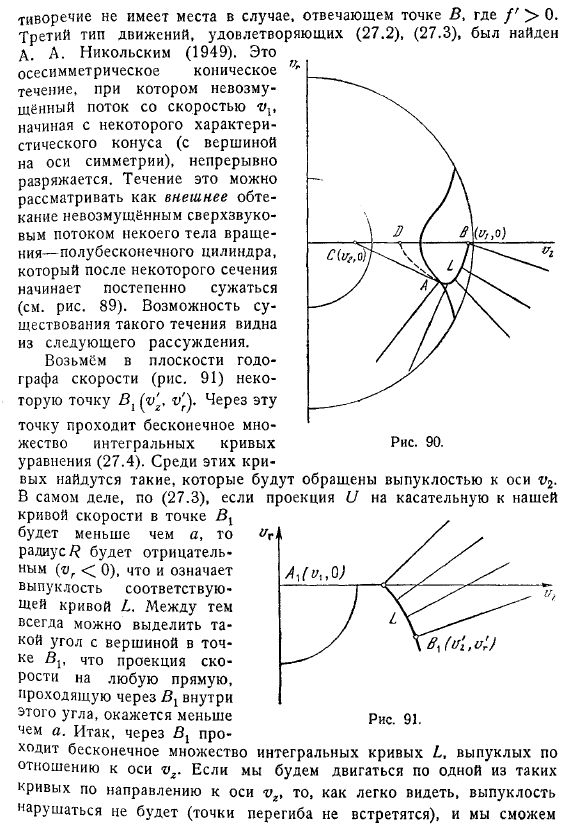
Эту дугу радиуса нарисованной нами окружности убираем как координаты точки m. Теперь снова направляемся к (27.3) . Он состоит из радиуса кривизны в точке m, центра кривизны ex и др. Рассмотрим задачу обтекания конуса. Уравнение А. А. Никольского также изучало движение годографического пространства к любой поверхности или в конечном итоге.
В последнем случае получается обобщение тех случаев плоских течений, в которых годографом служили эпициклоиды . Людмила Фирмаль
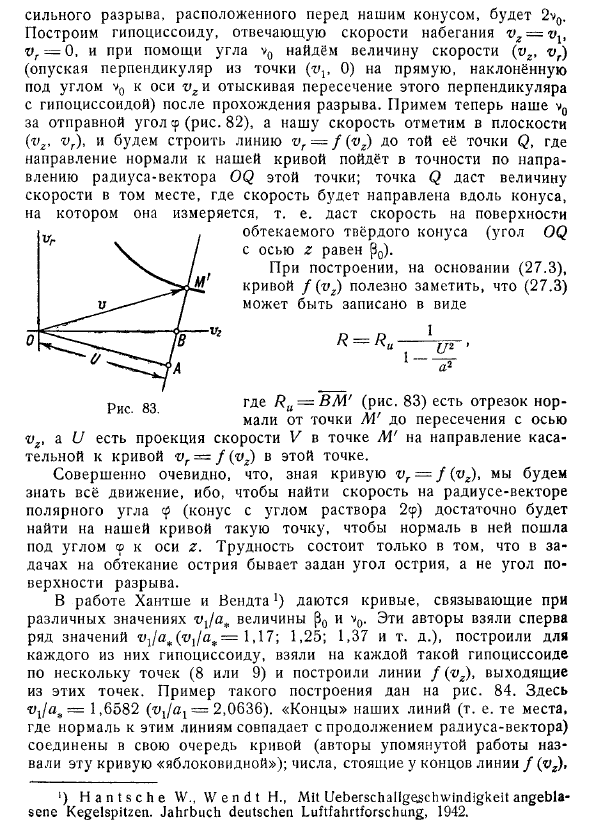
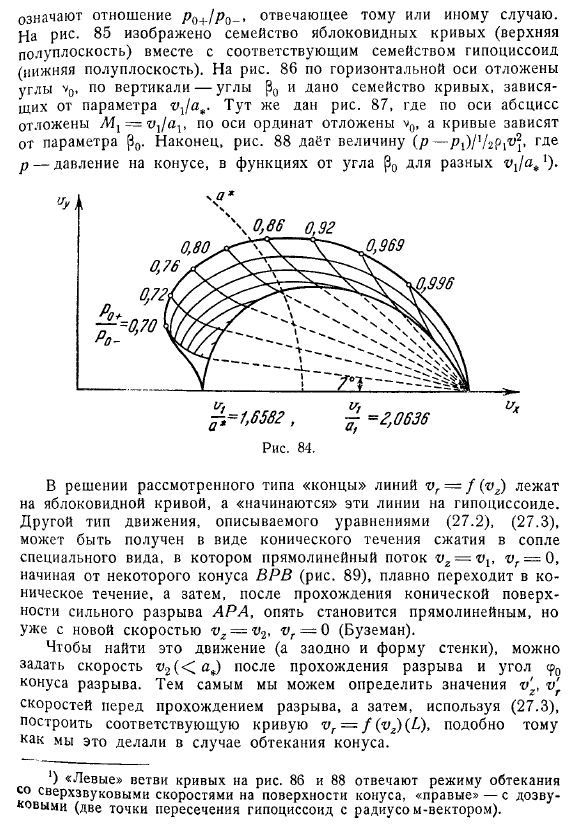
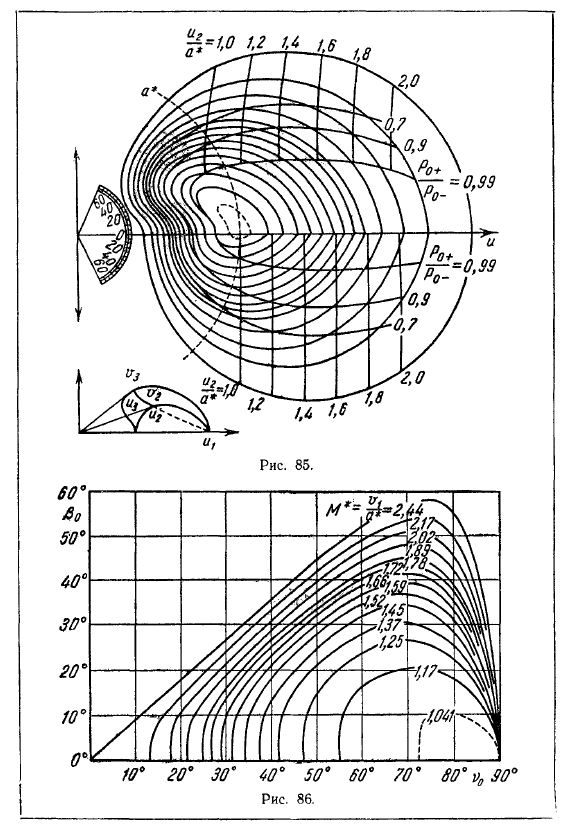
- Аналогичный результат можно увидеть в полученном Валландером и Жерменом. Сильный зазор перед конусом будет равен 2h0. Создайте гипокосоид, соответствующий скорости бега найти величину скорости, используя, что точка построена в направлении радиус-вектора этой точки. Точка 3 указывает величину скорости точки, в которой скорость направлена вдоль измеряемого конуса. То есть он указывает на скорость поверхности.
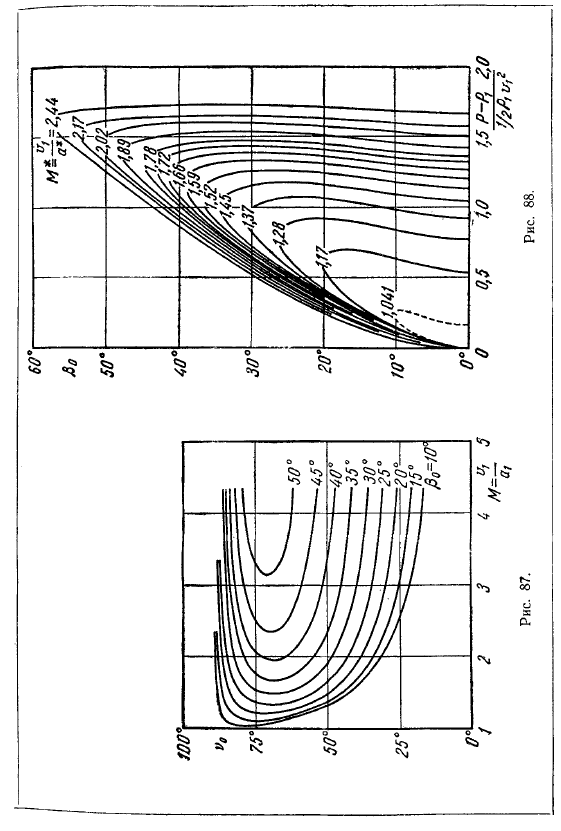
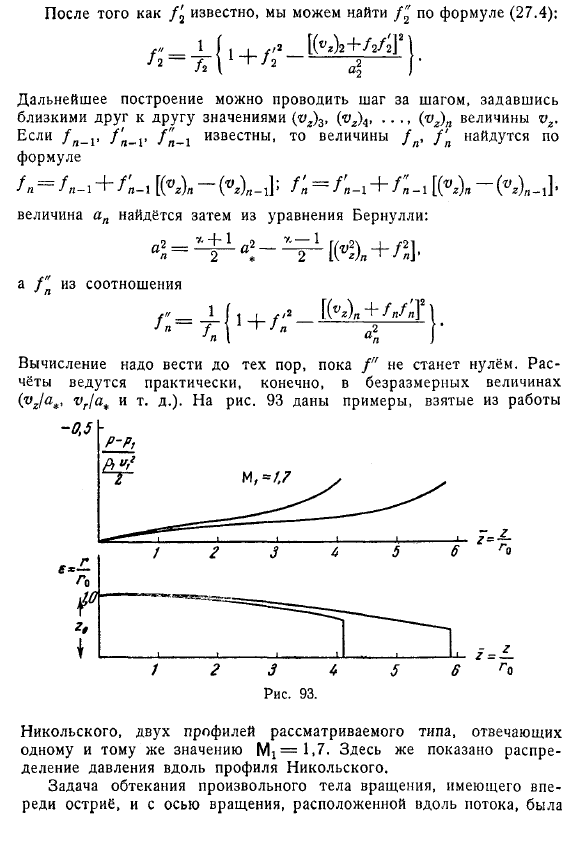
Обтекаемый конус (угол 00 с осью z равен Р0). При построении кривой на основе (27.3) отметим, что (27.3) можно описать в виде ki-vm (рис. 83) — нормальный отрезок от точки m до пересечения с осью vr o-скорость v в точке m в касательном направлении кривой в этой точке. Единственная проблема заключается в том, что поток вокруг наконечника определяет угол наконечника, а не угол прерывистой поверхности.

