Оглавление:




Ось стержня была первоначально дугой окружности
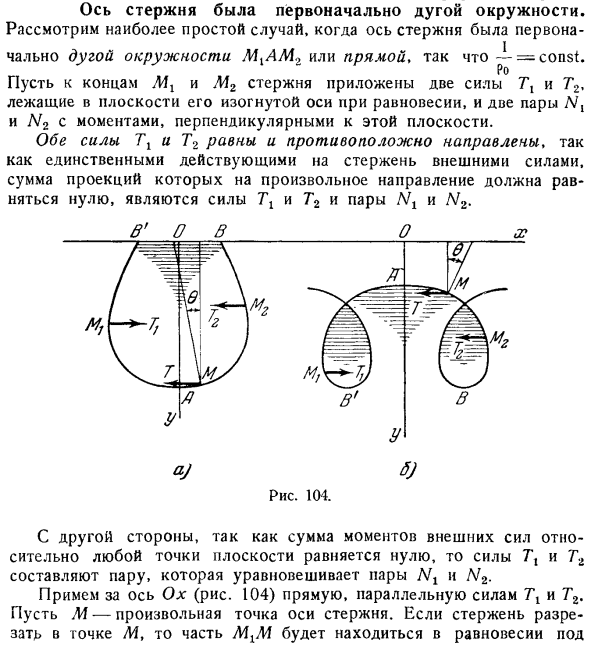
- Рассмотрим простейший случай, когда ось стержня изначально была дугой дуги L11AL1. Или, потому что это прямая линия, = const. Давай сделаем это. Предположим, что 2 силы 7 и T2 приложены к концу стержня и A42, которые находятся в равновесии в плоскости его изогнутой оси, а 2 пары и N2 моменты, перпендикулярные этой плоскости. Поскольку единственная внешняя сила, действующая на стержень, полная проекция которого в любом направлении должна быть равна нулю, это сила 7 и T2 и пара и N2, то силы 7 и T2 направлены одинаково и в противоположных направлениях.
Рисунок 104. С другой стороны, поскольку сумма моментов внешней силы в любой точке плоскости равна нулю, силы 7 и T2 составляют пару, уравновешивающую пару 1 и N2. Возьмем прямую линию, параллельную силам 7 и T2 для оси Ox рис.104. Пусть Л4 любая точка на оси стержня. Когда стержень разрезан в точке M, деталь будет находиться в равновесии под действием следующих внешних сил: 1 Сила 7 и пара Nv, действующая в конце M , 2 Сила T и пара N. В паре N существует момент Эти внешние силы, приложенные к дуге, уравновешиваются. Итак, сила Т имеет ту же величину, что и сила D, но направлена она в противоположную сторону.
В частности, для однородной фигуры, отнесенной к прямоугольным декартовым координатам, формулы принимают вид где одно интегрирование всегда может быть выполнено. Людмила Фирмаль
С другой стороны, сумма моментов всех внешних сил для любой точки на плоскости должна быть равна нулю. Получает суммы моменты, связанные с точкой О. затем, в ордината Y и точку автофокусировки Tlyl Тая Н + Н = От Или замените 7 и N из T на это значение 1, чтобы получить уравнение я = о. Если сила То есть, если к концу стержня приложить только пару, то из этого уравнения получим постоянную величину 1 p, а фигура вынужденного равновесия будет представлять собой еще одну дугу. Отдельно в этом случае мы решаем уравнение 1 p и берем 1 B в качестве фактора вне скобки с правой стороны результата. Получаем уравнение вида 1 1 7 7 = 0.
C2 указывает на положительную константу BfTx, а указывает на другие константы. на оси x последняя константа всегда исчезает, и уравнение равновесия Таким образом, получается дифференциальное уравнение кривой, форму которой принимает ось rod. To интегрируем это уравнение, нормаль в точке L1 и угол, под которым образуется ось Oy, показаны в повороте 6 рис. 104.Когда точка M перемещается в ds, нормали поворачиваются на угол DB и выглядят так: 1 2 ДС р 3 Оттуда, дифференциация, мы получаем З dy ДС ДС С2 г л ДХ л Потому что = sin U и j = cos 0 Как ДС Умножьте обе части уравнения. S 2 = cos0 + где произвольная константа. ДХ Косинус 0 ДС Т. 3 На и integration.
Использование DTI ДС = Р= 1л 2 cos0p. Узнайте сейчас cos0. 4 Откуда 5 Добавлять константу не нужно, так как в качестве оси Oy можно выбрать Нормаль кривой, перпендикулярную оси Ox. С другой стороны, у нас есть = г = С2 = + с 2 потому что о 4 п. это не так. Всегда. 6 Формулы 5 и 6 определяют x и y функции 0.Здесь нам нужно различать 3 случая в зависимости от того, является ли p или not. It будет находиться в пределах промежутка 1,+ 1 или больше, чем 1 или 1. Форма кривой в этих 3 случаях кратко показана.
- Анализ основан на следующих комментариях. Согласитесь считать дугу S кривой из точки A на оси Oy р.104, в качестве положительного направления 5, первоначально делают направление точки, где абсцисса равна нулю. Когда кривая описывается в этом направлении, всегда будет increase. So ds всегда положителен в выражении 4 радикалы всегда имеют тот же знак, что и rfO. Этот знак радикала следует сохранить во всех последующих формулах.
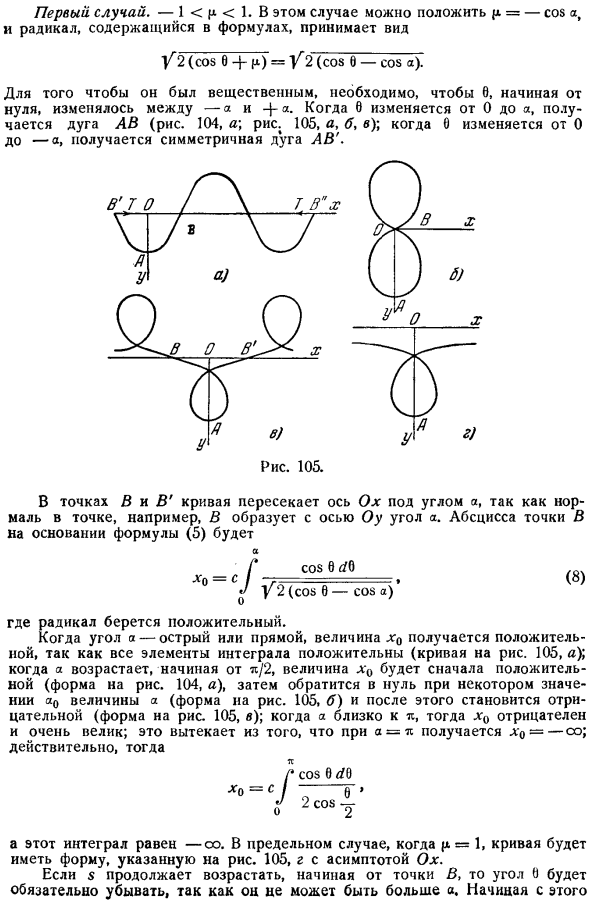
Из формулы ды ДХ d7 = синус 77 = cos8 7 с увеличением s мы можем видеть, что координаты y и x увеличиваются или уменьшаются со значением—sinO и cos 6 положительные или отрицательные. Наконец, точка перегиба это точка кривой, которая пересекает ось x из уравнения 2.Указывает, что p бесконечно при y = 0 и наоборот. Ось Oy это ось симметрии кривой. Первый случай. 1 q 1.In в этом случае можно поставить q = cos, и радикалы, содержащиеся в Формуле, примут следующий вид: В2 Кос 6 4 П = П2 потому что О потому что. Для того, чтобы он был подлинным, необходимо начать с 6 Для точек B и B кривая пересекается с осью Ox и углом a. это связано с тем, что, например, Нормаль точки образует ось Oy и угол a.
В самом деле, отнесем плоскую кривую к оси вращения, принятой за ось Ох, и перпендикулярно к последней направим ось Оу. Людмила Фирмаль
Абсцисса точки B на основе уравнения 5 выглядит следующим образом: Но… Семь cos0 РФО 1 2 cos 6 COS a 8 Здесь экстремисты настроены позитивно. Если угол a является острым углом или прямой линией, то значение x0 является положительным, поскольку все элементы Интеграла положительны кривая на рис. 105, а. когда A, начиная с 2, увеличивается, то величина n0 сначала становится положительной в виде рисунка 104, а, затем исчезает с определенным значением величины A0 в виде рисунка 105, Б, а затем становится отрицательной в виде 105, Б если a близко к tf, то она становится очень отрицательной. Это вытекает из того, что если a = MC, то п0 = со. Действительно.
Я потому что 6 РФО И этот Интеграл равен to co. In в ограниченном случае, если q = 1, кривая имеет форму, показанную на рисунке. 105, включая асимптоту быка. если s начинается из точки B и продолжает увеличиваться, угол 0 неизбежно уменьшится. это потому, что вы не можете сделать его больше, чем a. с этого момента необходимо поставить знак минус перед радикалами. Когда 0 изменяется от a до a, мы получаем новую ветвь первой и симметричной кривой относительно B. подобно синусоиде, вы получаете бесконечное число одинаковых волнообразных линий. 2 й случай. для p 1, 0 изменяется от 0 до 2k. 1 с вами Это никогда не проходит. Кривая имеет вид, показанный на рис. 104, б.
Интеграция в этих 2 случаях может быть выполнена с помощью эллиптических функций см. Appell и Lyacour, принцип принципа, эллипс, приложение. 3 й case. In в среднем случае, при p = 1, Как уже упоминалось, кривая имеет ось Ox в качестве асимптоты, так как x0 = co рис. 105, d.
Смотрите также:
Решение задач по теоретической механике
| Рефракция | Случай первоначально прямолинейного стержня, сжимаемого на концах двумя одинаковыми и прямо противоположными силами |
| Натяжение и изгибающий момент | Плоские эластики. Упражнения |

