Ориентируемые и неориентируемые поверхности

Оглавление:

Ориентируемые и неориентируемые поверхности

Ориентируемые и неориентируемые поверхности. Следующая задача-определить понятие направления склеиваемой поверхности от параметрически заданной поверхности. В этом случае выбор непрерывной единичной нормали на поверхности для определения направления неудобен, даже если имеется не более одной точки, а также можно понять, что непрерывность нормали зависит от пространственной точки (а не от параметра склеиваемой поверхности).Это может быть нарушением гладкости поверхности кривой, на которой происходит сцепление. Например, часть 204 поверхности двугранного угла, показанная на рисунке, может быть рассмотрена как результат склеивания 2 равных прямоугольников.

Если вы стремитесь вдоль разных поверхностей к одной и той же точке в конце этого угла, соответствующие единичные пределы нормали будут разными. Людмила Фирмаль

Ниже показано определение ориентируемой поверхности, которую эта поверхность может ориентировать. Когда поверхность склеивается «гладким способом» (то есть в случае кривых, в которых происходит склеивание, единичные нормали могут быть выбраны в каждой точке, поэтому граница хорошо подобранных 2 нормалей вблизи этой точки) адгезивная поверхность может быть качественно новой особенностью, которая отображается на адгезивной поверхности. В отличие от параметрической поверхности, в этом случае непрерывные единичные нормали не всегда выбираются по всей поверхности. surface. An примером такой поверхности является так называемая Лента Мебиуса**.

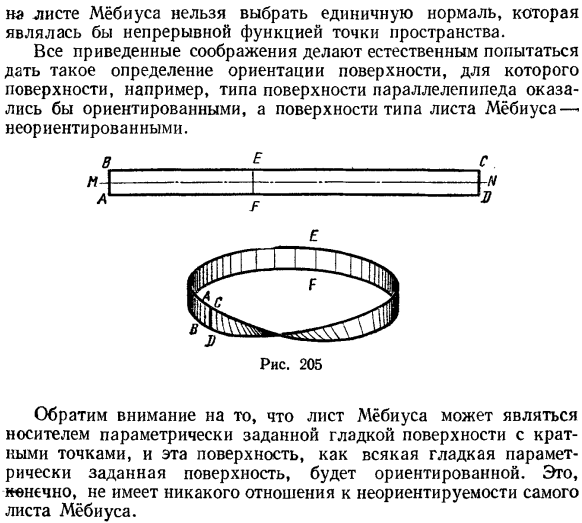
Возьмите прямоугольную полоску бумаги ABCO, поверните вокруг оси симметрии We параллельно сторонам BC и AE и приклейте край AB к совместному предприятию, которое вы получите(рис.205). Но при таком способе формирования пояс Мебиуса получается путем приклеивания поверхности к себе. Однако, как описано в определении 22, нетрудно склеить и получить 2 прямоугольника ABER и RESO (см. Рисунок 205). 1 особенность ленты Мебиуса заключается в том, что есть только 1″сторона».нельзя красить одну сторону красным, другую синим, например, стороной цилиндра. Также * «А, Ф, Мебиус (1790-1868) немецкий математик и астроном. Шесть * $50.Элементы теории поверхности 260.

Полоса Мебиуса не позволяет выбрать единичную Нормаль, которая является непрерывной функцией точки в пространстве. Людмила Фирмаль

Все вышеперечисленные соображения делают естественным попытку определить направление поверхности, например, поверхность, подобная поверхности параллелепипеда, ориентирована, а поверхность, подобная полосе Мебиуса, не ориентирована. Что Е /Я / Л Обратите внимание, что полоса Мебиуса является параметрически заданной опорой гладкой поверхности с несколькими точками, и эта поверхность плавно ориентирована таким же образом, как и параметрически заданная поверхность. Конечно, это не касается направления самой полосы Мебиуса.

Ориентация гладкой поверхности.	Второй подход к понятию ориентации поверхности.
Склеивание поверхностей.	Определение и свойства поверхностных интегралов.