Оглавление:




Опытное исследование кручения
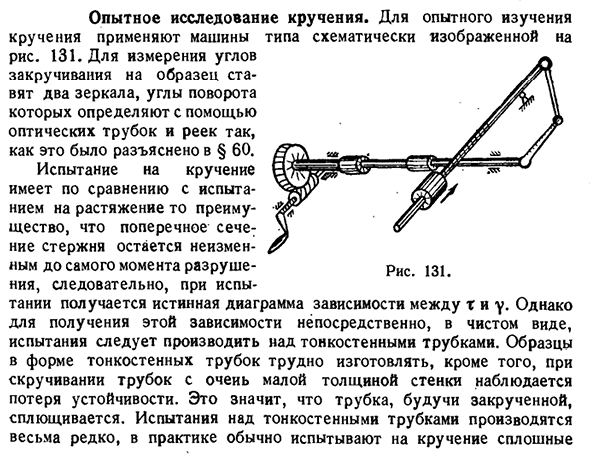
- Экспериментальное исследование кручения. Для экспериментальных исследований Машина кручения прикладывает диаграмму. 1 3 1.To измеряют угол кручения, на образец помещают два зеркала, а угол поворота определяют с помощью оптической трубки и рельса, как описано в§ 60. Испытание на кручение имеет преимущество перед
испытанием на растяжение, что поперечное сечение стержня не изменится- Тип схематично нарисован на До момента разрушения-фигура. Таким образом, при проверке получается истинная диаграмма соотношения между t и Y.
Но чтобы получить это соотношение непосредственно, в чистом виде, необходимо провести Людмила Фирмаль
испытания на тонкостенных трубках. Образец в виде тонкостенной трубки трудно изготовить, кроме того, при скручивании трубки с очень тонкой толщиной стенки теряется стабильность. Это означает, что скручивающая трубка будет плоской. Испытания тонкостенных труб на самом деле проводятся очень редко, но обычно они проводятся для скручивания твердого тела на кручение[CHAP. VII Образец круглого сечения.
Сам тест может преследовать различные цели, такие как: 1. Чтобы определить модуль сдвига, крутящий момент увеличивается поэтапно и угол кручения стержня измеряется каждый раз. В упругой области угол кручения и крутящий момент связаны соотношением Здесь i-расстояние между зеркалами, то есть длина, на которой измеряется угол скручивания. Применяя эту формулу к приращениям этих величин на каждой ступени нагрузки, вместо применения к углу кручения и крутящему моменту получаем::
- Для компенсации возможных погрешностей измерения модуля сдвига среднее значение берется из ряда значений, полученных для различных стадий нагружения. 2. Для расчета пластического диапазона график t-u является основным и исходным материалом. В результате торсионного эксперимента была получена зависимость между моментом M и углом кручения R.
Для гипотезы плоского сечения, как показано в§ 87, y=FR. Таким образом, g=g (yr). Подставляя уравнение равновесия, получаем: Г М=J Т(Г Р)Г Д Ф=2л т(г) г * ДГ. (93.2) Ф » Теперь давайте введем обозначения: Т и в определяются непосредственно из опыта, когда происходит сдвиг на поверхности стержня. Вместо рисунок M — <р, можно рассматривать данный показатель Т-ц0. С другой стороны, она получается из уравнения (93.2): (93.3) Различают(93.3) по u0: (93.4)§ 93]экспериментальное исследование кручения 203 Исключим Интеграл из уравнений (93.3) и(93.4). Возьми: т(г)=г^4-3/б.(93.5) Здесь мы опускаем индекс y величины y. таким образом, чтобы определить зависимость t от любого из них, измените масштаб так, чтобы вместо момента было отложено время, деленное на константу 2π
, а затем, чтобы построить производную функции T и точку формулы(93.5) Людмила Фирмаль
(искомая зависимость t от do). Следует отметить, что кривая T более крутая и гладкая, чем кривая из. Поэтому определить пропорциональный предел или предел текучести фигуры кручения труднее, чем показатель растяжения. В настоящей работе предлагается способ обработки торсионного волочения цилиндрического стержня для получения t-y диаграмм с помощью Nadai. Модификация этого метода принадлежит Хиллу и состоит в следующем: если у вас есть кривая зависимости t от Y, то легко построить кривую зависимости y от Y.: T (Y)=Y* ^ ( 7 ) + 4/«. (93.6) Графическим дифференциалом кривой зависимости y от Y является кривая y. зависимая кривая от 3
дает более точные результаты, чем производная от t. если добавить достаточно большой крутящий момент, то спиральный образец будет разрушен. Характер разрушения зависит от материала. Образцы, изготовленные из пластика, обычно разрушаются за счет поперечной резки, то есть поперечного сечения, под которым действует основное касательное напряжение. Точно такая же величина тангенциального напряжения действует на продольные сечения брусков благодаря закону четности, так что скрученные деревянные бруски делятся вдоль волокон. Наконец, при скручивании стержней из такого хрупкого материала, как чугун, возникает характерный косой излом. Как известно, чугун обладает низким
сопротивлением отрыву, а напряженное состояние чистого сдвига в бесконечно малых элементах скрученного стержня составляет 45 ° 132 относительно оси стержня). Таким образом, существует семейство винтовых поверхностей, которые пересекают кручения образующих 204[глава. VII Под углом 45°как семья, присутствующая в другом месте — Райс, 132. Принимая переходное сопротивление в качестве меры прочности торсионного материала, он основывается на предположении, что это определение является условным и распределение напряжений до момента разрушения остается таким же, как и в упругой области. Поэтому величина временного сопротивления кручению является условной характеристикой, имеющей только «сравнительное значение».
Смотрите также:
| Кручение тонкостенных стержней открытого профили | Предельное состояние закрученного стержня из идеально-пластического материала |
| Кручение упругих стержней сплошного профиля | Основные определения |

