Оглавление:
Определённый интеграл и основные свойства
Пусть функция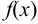 
определена на 
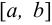. Разобьём отрезок на 
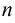частей точками 
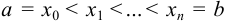. На каждом из частичных отрезков 
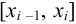возьмём произвольную точку 
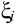, и составим сумму
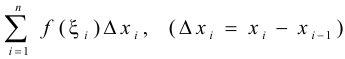, которая называется интегральной суммой функции 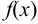на отрезке .
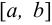Предел интегральной суммы, при условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремится к 0, называется определённым интегралом функции 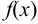в пределах от 
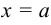до 
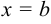и обозначается
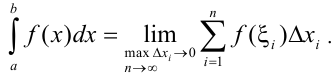
Геометрический смысл определенного интеграла состоит в том, что он выражает площадь некоторой криволинейной трапеции на .
Физический смысл определенного интеграла состоит в том, что он выражает работу некоторой переменной силы в данном участке.
Основные свойства определённого интеграла
1) 
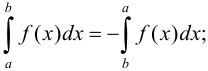
2) 
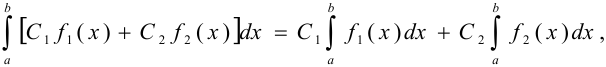где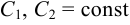 
;
3) 
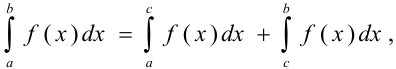
где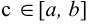 
или точка, лежащая вне ;
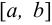4) 
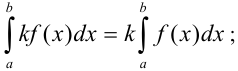
5) 
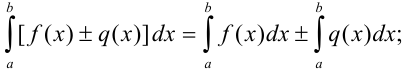
6) если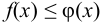 
при 
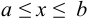, то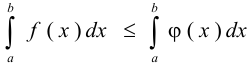 
;
7) если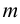 
— наименьшее, а 
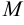— наибольшее значения функции 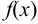на отрезке 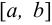, то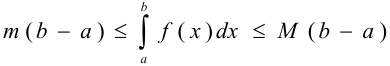 
;
8) если функция 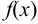непрерывна на отрезке , 
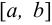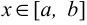, то на этом отрезке найдётся такая точка 
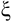, что
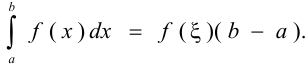
Формула Ньютона-Лейбница
Если функция 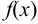непрерывна на отрезке 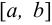и для неё известен неопределённый интеграл: 
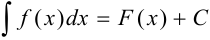, где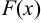 
— первообразная функции 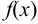, то определённый интеграл может быть вычислен по формуле Ньютона-Лейбница:
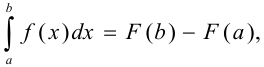
т. е. определённый интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования. При вычислениях пишут следующим образом:
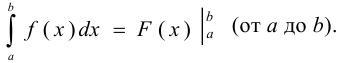
Для вычисления определенного интеграла на 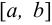необходимо найти некоторую первообразную по отношению к подынтегральной функции и вычислить разность значений этой первообразной в точках 
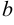и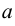 
. Эта разность будет равна определенному интегралу на .
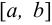Задача №92.
Вычислить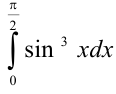 
.
Решение:
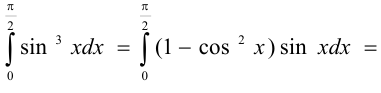
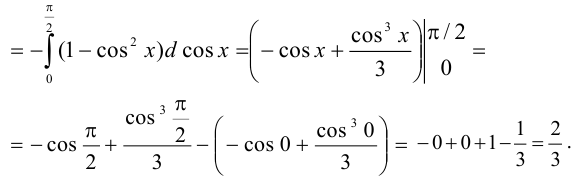
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
