Оглавление:
Определители
Пусть дана квадратная матрица
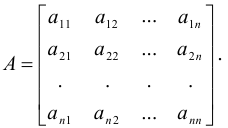
Определителем (детерминантом) матрицы  называют число, которое ставится в соответствие данной матрице и обозначается
называют число, которое ставится в соответствие данной матрице и обозначается
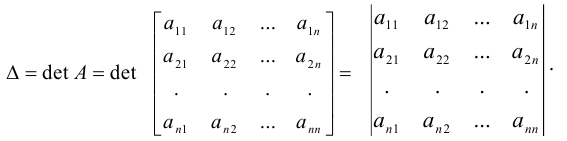
Определитель матрицы второго порядка
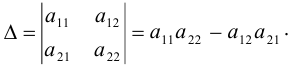
Если в квадратной матрице 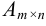 вычеркнуть
вычеркнуть 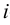 -ю строку и
-ю строку и 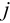 -ый столбец, то получим матрицу
-ый столбец, то получим матрицу 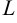 размера
размера 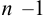 . Определитель этой матрицы
. Определитель этой матрицы 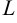 называется минором элемента
называется минором элемента 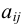 и обозначается
и обозначается 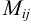 .
.
Алгебраическим дополнением 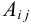 элемента
элемента 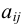 называется минор этого элемента, умноженный на
называется минор этого элемента, умноженный на 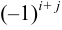 , т. е.
, т. е.
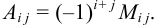
Теорема. Сумма произведений элементов какой-нибудь строки (столбца) на их алгебраические дополнения равна определителю матрицы. Сумма же произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю.
Воспользовавшись этой теоремой, найдем определитель матрицы третьего порядка:
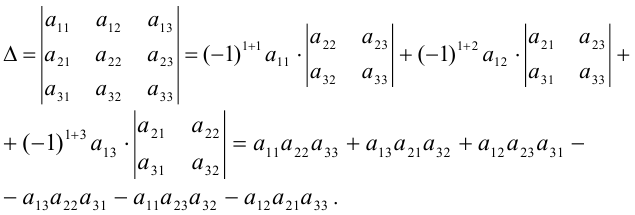
Вычисление определителей n-го порядка
Всякие 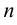 чисел, расположенные в определенном порядке, образуют перестановку. Меняя порядок расположения цифр в перестановке, получим другую перестановку. Всего перестановок из
чисел, расположенные в определенном порядке, образуют перестановку. Меняя порядок расположения цифр в перестановке, получим другую перестановку. Всего перестановок из 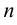 чисел —
чисел —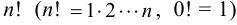 . Если в перестановке меньшее число следует за большим, то говорят, что имеется инверсия. Перестановка из
. Если в перестановке меньшее число следует за большим, то говорят, что имеется инверсия. Перестановка из 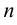 -элементов называется четной, если число инверсий в ней четно и нечетной, если оно нечетно.
-элементов называется четной, если число инверсий в ней четно и нечетной, если оно нечетно.
Пусть дана матрица
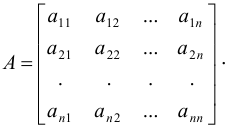
Определителем 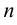 -го порядка квадратной матрицы
-го порядка квадратной матрицы  называется алгебраическая сумма
называется алгебраическая сумма 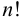 -слагаемых вида
-слагаемых вида 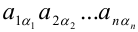 , состоящих из
, состоящих из 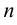 сомножителей, взятых по одному из каждой строки и из каждого столбца. При этом слагаемые, у которых вторые индексы сомножителей
сомножителей, взятых по одному из каждой строки и из каждого столбца. При этом слагаемые, у которых вторые индексы сомножителей 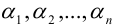 образуют четную перестановку, берутся со знаком «+», нечетную перестановку — со знаком «-». Таким образом,
образуют четную перестановку, берутся со знаком «+», нечетную перестановку — со знаком «-». Таким образом, 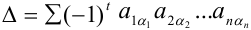 , где
, где 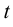 — число инверсий в перестановке (
— число инверсий в перестановке (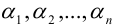 ).
).
Свойства определителей n-го порядка
- При замене строк столбцами определитель не меняется.
- При перестановке двух строк определитель меняет знак.
- Если все элементы какой-нибудь строки равны нулю, то определитель равен нулю.
- Если элементы строки умножить (разделить) на число
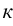 , то значение определителя увеличится (уменьшится) в
, то значение определителя увеличится (уменьшится) в 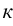 -раз.
-раз. - Если матрица имеет две одинаковые или пропорциональные строки, то ее определитель равен нулю.
- Если элементы какой-либо строки матрицы представляют собой сумму слагаемых, то определитель этой матрицы равен сумме двух определителей соответствующих матриц.
Определитель 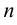 -го порядка вычисляется путем приведения его к треугольному виду. Метод вычисления определителя путем приведения к треугольному виду заключается в том, что, используя свойства определителей, приводят его к виду
-го порядка вычисляется путем приведения его к треугольному виду. Метод вычисления определителя путем приведения к треугольному виду заключается в том, что, используя свойства определителей, приводят его к виду
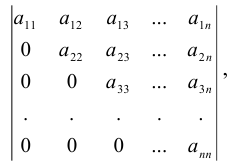
который называется треугольным. Очевидно, что
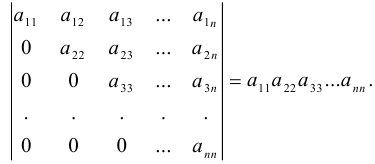
Задача №3.
Дана матрица
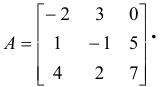
Найти алгебраические дополнения элементов второго столбца.
Решение:

Задача №4.
Вычислить определитель
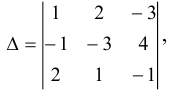
преобразовав его так, чтобы два элемента некоторого ряда равнялись нулю, и разлагая полученный определитель по элементам этого ряда.
Решение:
Используя свойства определителей, преобразуем данный определитель следующим образом: к первой строке прибавим вторую, а к третьей — вторую, умноженную на 2. Получим
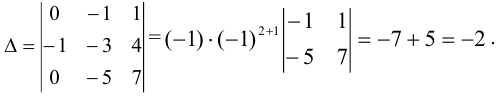
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Обратная матрица с решением задачи |
| Ранг матрицы задачи с решением |
| Операции над матрицами задачи с решением |
| Применение рядов в приближенных вычислениях задачи с решением |

