Определители (основные понятия)

Определители (основные понятия)

• ОПРЕДЕЛИТЕЛИ (основная концепция) Детерминанты широко используются в различных областях математики и их приложений, особенно при решении систем линейных алгебраических уравнений. выражение = «11» 22 ~ «21» 12 «А» 12 «21» 22 D = Это называется квадратичным определителем. Символ cij называется определяющим элементом, первый индекс r указывает номер строки, а другой индекс j указывает номер столбца, где этот элемент пересекается.

Расчет квадратичного определителя обозначен схемой. •• -3 б потому что грех а-грех а потому D = XI-X То есть произведение вторичных элементов вычитается из произведения основных диагональных элементов. Пример: = 2,6-5 — (- 3) «12 — (- 15) = 27; = cos2 a + sin2 a = 1. выражение «11» 12 «13» 21 «22» 23 «31» 32 «33 = 0-22 ^ 33 + ^ 12 ^ 23 ^ 31 + ^ 21 ^ 32 ^ 13-Я31а22й13-021 ^ 12 ^ 33 «-» 32 ^ 23 ^ 11 Это называется кубическим определителем. Элементы an, a-22, <* s3 образуют основную диагональ определителя, а элемент a3b 022 «» 13 является квадратичным.

Верхний элемент и а22 образуют главную диагональ определителя. «21» и «12» являются случайными. Людмила Фирмаль

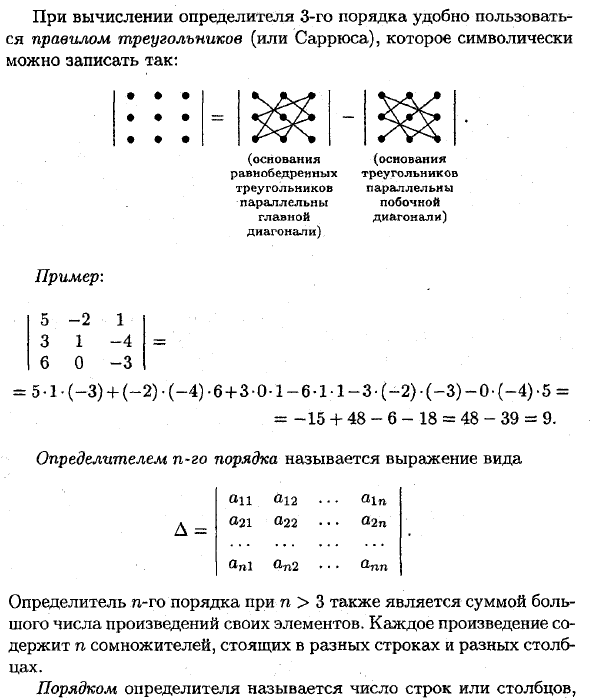
При вычислении кубического определителя полезно использовать правило треугольника (или Саррюса), которое можно символически описать следующим образом: •••••• (Основание равнобедренного треугольника параллельно главной диагонали) (Основание треугольника параллельно боковой диагонали) Пример: 5-2 1 3 1 -4 6 0-3 5-1 • (-3) + (-2) — (- 4) ‘b + 3-0-1-b-M-3’ (-2) — (- 3) -0 ‘(-4)’ 5 = -15 + 48-6-18 = 48-39 = 9.

Определитель n-го порядка является выражением вида sc и a21 022 Up \ Up 2 1 р CL2n (Bottle A = Определитель n-го порядка mri n> 3 также является суммой многих произведений его элементов. Каждый продукт содержит n факторов в разных строках и столбцах. Окончательный порядок — это количество строк или столбцов.

• Всегда одинаковое количество. , Определитель n-го порядка имеет n строк (и столько же столбцов). Определитель n-го порядка может быть вычислен путем непрерывного уменьшения порядка определителя.

В этом случае используются свойства определителя (см., В частности, Расширение определителя для элементов определенной серии). Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Некоторые дифференциальные уравнения, встречающиеся в механике	Свойства определителей
Движение точки на плоскости. Система дифференциальных уравнений	Матрицы (основные понятия)