Определители любого порядка

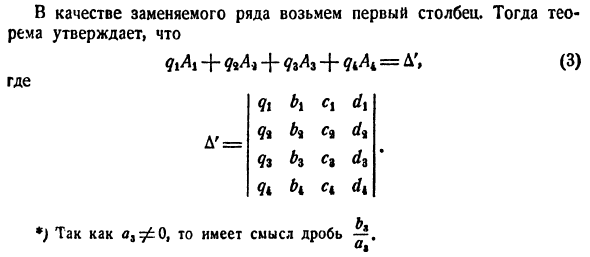
Определители любого порядка

• Получить первый столбец в качестве заменяемой строки. Тогда теорема I \ A 1 + + Yr & r + Yak \ = A ‘, (3) где Я \ b \ s \ b <i d} Яг ч сг дз D ‘= Як БК ЦК День Это имеет смысл, так как oa -jbQ ~ Чтобы проверить правильность (3), разложите A ‘на элементы первого столбца. A ‘= qiQi. + G% Q% + I A + (4) Здесь, как обычно, Q |, Qa, Qt и Q4 — алгебраические дополнения чисел Yan и Ya * Yak. • Qj получается путем удаления первого столбца (и первого ряда) из A. B% d) d% qi = ca d3 bk ck То есть Q = i4 |. Аналогично (E4 = La, Q3 = 4a, Qi = Ak. Замена Qn, Qa, Q8, Q4 на A \, A%, A ^ A4 в Q дает (3).

Теорема об аннулировании. Сумма произведений некоторых пар детерминантных элементов в алгебраическом дополнении параллельного ряда равна нулю. Для наглядности поговорим о детерминантах (2). Например, d \ Ax + d% A% + + di ^ i = На самом деле, согласно теореме замещения, сумма, написанная слева, равна определителю дт бх A ‘= г, рф, DQ BC дт бт с, рф, BK CK DK

\ dt % колонка Ag DT ди Получить из А, заменив столбец Но опредaеленно И теорема доказана. , пересекающегося с предыдущим элементом. Этот минор, умноженный на (- ) p, где p — общее количество зачеркиваний, называется алгебраическим дополнением того же элемента.

о Минор любого элемента матрицы является кубическим определителем, генерируемым матрицей, полученной из (1) путем удаления ряда Людмила Фирмаль

Например, второстепенный элемент 3 элемента d3 — это тот же определитель, умноженный на (-1) 7 = -1. Где p = (поскольку d3 находится на пересечении четвертого столбца и третьего ряда). Лемма. Сумма произведения любой пары элементов в любом ряду матрицы (1) на алгебраическое сложение не зависит от выбора ряда. Например Mi + M «+ Mz» b Mi = Ms + b, Br + csC3 + Мы принимаем эту важную лемму без доказательства. Определитель четвертого порядка, соответствующий матрице определения (1), является суммой парного произведения ряда элементов матрицы в алгебраическом дополнении.

Этот идентификатор О, БХ, ДХ, ДХ ау б} ди ag bs eat / 3 ай бк ск дл Конечно, приведенное выше определение является законным благодаря предыдущей лемме. Поэтому, зная, что такое определитель третьего порядка, мы смогли ввести понятие определителя четвертого порядка. Однако такие детерминанты, как 5-й и 6-й, могут быть введены точно таким же образом. В общем случае n-й определитель, соответствующий конкретной матрице (n-й порядок), является суммой парных произведений элементов любого ряда этой матрицы на алгебраическое дополнение.

• Важно, что эта сумма не зависит от выбора серии. Последнее принимается без доказательств. № 2. Основное свойство определителя. Их расчет. Теорема Любой определитель степени имеет те же характеристики I-VI, что и определители второго и третьего порядка (см. § 1, № 2 и § 2, № 2).

Эта теорема принимает без доказательства. Вот расчет определителя. Пусть Нед найдет 2 6 3 0 д-4 7 6 2 ~~ 5 1 10 ‘ 3 2-10 Этот определитель имеет одну особенность. Все элементы в четвертом столбце, кроме одного, равны нулю. Поэтому, если вы расширите D до четвертого элемента столбца, вы получите только один *) (а не четыре, как в общем случае!). 2 6 = 2 (-2 -f-30 -f-18-9 -J-30-4) = 126. D = 2 5 1 3 2-1

Теперь рассмотрим детерминанты 4 6 7 0 2 1 3 3 5 Хотя это не «полезно», его легко изменить на «полезное», используя свойство VI. То есть вычтите третий столбец, удвоенный из второго столбца. Как известно, это не влияет на значение определителя **).

Давайте согласимся, что мы называем «определитель» определителем, который содержит ряд, в котором все элементы, кроме одного, равны нулю. Людмила Фирмаль

В результате А потом. 4-8 7 D = 0 0v 1 3-7 ^ 5 ♦) Обратите внимание, что p = Ck существует в элементе 2 четвертого столбца. ••) Свойство VI: «Вычитание добавляет серию вместо n, но добавленную серию можно умножить на любое число, например -2, поэтому между сложением и вычитанием нет никакой разницы.

И здесь уже написано на правой стороне. Удобные «детерминанты. Разложение с элементами во второй строке ) D = Вот еще один пример: 4-8 1 2 3-7 _4 3 7 = 4 4 3 5 7 2 2 6 5 3 D == A = Если вы вытащите второй ряд из третьего ряда, 4 3 2 7 2 O 6 5-2 Добавьте первую строку к третьей. 4 3 2 D = 7 2 0 10 8 0 Результат является полезным определителем.

Разложение на элементы в третьем столбце 7 2 = 2 (56-20) = 72,108 В ‘ D = 2 D = Демонстрирует, что любой определитель может быть удобно использован с помощью Property VI. 1 ‘). Дай мне < я, ди a2 bt ca d3 o »btc®d% би кт ди

В любой выбранной строке убедитесь, что все элементы, кроме одного, вероятно, равны нулю. Для наглядности пусть будет третий запас. Очевидно, A = 0, если все элементы в этой строке равны нулю. За исключением этого тривиального случая ***), вы можете предположить, что один из элементов в третьей строке не равен нулю. Напрaимер, предположим, что это agph0. *) Удалено 4 из первого ряда и -1 из второго столбца. **)

Чтобы быть более точным, найдите что-то «удобное» эквивалентное ему. ***) В целом можно предположить, что в A нет рядов, состоящих целиком из нулей.Затем вычтите- *) из второго столбца Умножение первого столбца B \ Ох б \ Ой Ош дт дт д. či Ci D = Где b \ = bt-at ^ t = аи Вы можете видеть, что ноль отображался вместо bt на пересечении третьей строки и второго столбца. Вычтите первый столбец, умноженный на третий столбец -Заменить элемент на ноль.

Наконец-то Операции, замены и приводят к следующему формату для третьей строки В ООО, Другими словами, он становится «полезным * детерминантом». Замечания. В большинстве случаев определитель третьего порядка легче вычислить, приведя к «удобному * виду», чем правило Саррюса. № 3. Теорема о замене и теорема о недействительности. Следующие две теоремы очень важны. Теорема о замене. Пусть определитель степени -n. Сумма произведений пар алгебраических дополнений элементов любого ряда на любое число qlf Yar ••• »пn равна определителю ». Доказательство. Для наглядности n = 4 и ag bx su di % D% yts az bi g3 （/ 3 ai bk ck dk D =

Получить первый столбец в качестве заменяемой строки. Тогда теорема I \ A 1 + + Yr & r + Yak \ = A ‘, (3) где Я \ b \ s \ b <i d} Яг ч сг дз D ‘= Як БК ЦК День Это имеет смысл, так как oa -jbQ ~

Смотрите также:

Предмет высшая математика

Определители 2-го порядка	Решение систем линейных уравнений
Определители 3-го порядка	Векторы