Задача №4.
Определить силы, нагружающие стержни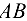 
и 
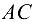кронштейна, удерживающего в равновесии груз 
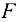= 6 кН и растянутую пружину, сила упругости которой 
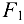= 2 кН. Весом частей конструкции, а также трением на блоке пренебречь (рис. 1.20, а).
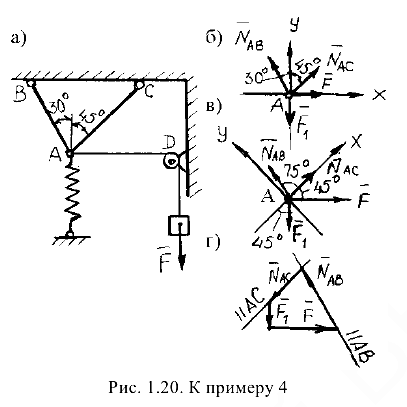
Решение:
Задачу решаем аналитическим методом. Рассматриваем равновесие точки схода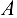 
. К ней приложены заданные активные силы — сила натяжения троса 
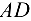, равная весу груза 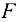и сила упругости пружины 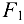. Так как и трос, и пружина растянуты, то эти силы направлены от точки 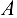. Рассматривая точку 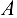как свободную, отбрасываем связи (стержн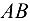и 
и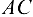 
), заменяя их действие реакциям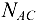и 
и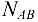 
. Реакции стержней направляем от точки 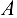, так как предварительно полагаем стержни растянутыми (действительные направления реакций стержней в начале решения неизвестны). Если наше предположение окажется неверным, то искомая реакция стержня получится в ответе со знаком «минус»; это говорит о том, что стержень сжат и истинное направление реакции — к точке 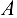. Полученная расчетная схема изображена на рис. 1.20, б.
Принимаем обычное вертикально-горизонтальное направление координатных осей. Для полученной плоской системы сходящихся сил составляем два уравнения равновесия:
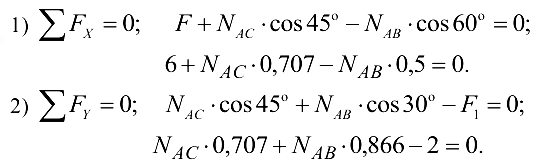
Решая полученную систему уравнений, находим 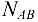=5,86кН и 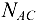=—4,34кН. Искомые силы, нагружающие стержни, по модулю равны найденным реакциям стержней, а по направлению противоположны им. Замечаем, что в соответствии с изложенным правилом стержень 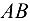оказался растянутым, а стержень 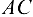— сжатым.
Следует отметить, что каждое из полученных уравнений равновесия содержало оба неизвестных, чего можно избежать, направив координатные оси по-другому — совместив одну из осей с неизвестной силой (рис. 1.20, в). При этом в уравнении равновесия для другой оси окажется лишь одно неизвестное:
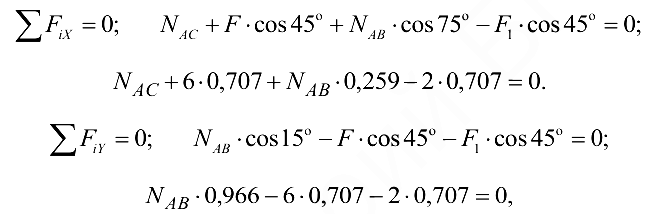
откуда
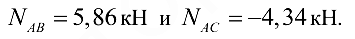
Для проверки правильности решения применяем графический метод — в выбранном масштабе строим замкнутый силовой многоугольник (рис. 1.20, г). От произвольной точки откладываем вектор заданной силы 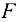от конца вектора 
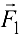— вектор заданной силы 
.
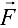Затем через начало и конец вектора проводим известные направления искомых реакций стержне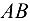й и 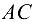. Стрелки, изображающие направления сил 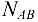и 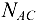, ставим таким образом, чтобы в векторном многоугольнике было единое направление обхода — в данном случае против часовой стрелки. Измеряя искомые векторы с учетом принятого масштаба, получаем
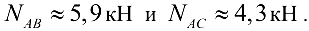
(Точность графического решения будет тем выше, чем крупнее принят масштаб построения). Следует отметить, что векторный многоугольник показывает действительное, а не предполагаемое направление искомых сил.
Ответ:
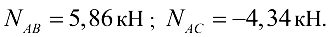
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
