Задача №14.
Определить положения мгновенного центра вращения и центроиды звена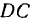 
шарнирного антипараллелограмма 
, большое звено которого 
остается неподвижным во все время движения, если известно, что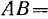 
.
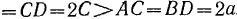Решение:
Точк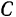а 
звена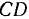 
может двигаться только по окружности с центром в точке 
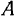. Поэтому скорость точки 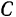всегда направлена ‘перпендикулярно к 
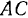, а мгновенный центр вращения расположен на продолжении прямой (рис. 31). Проводя аналогичные рассуждения, получим, что
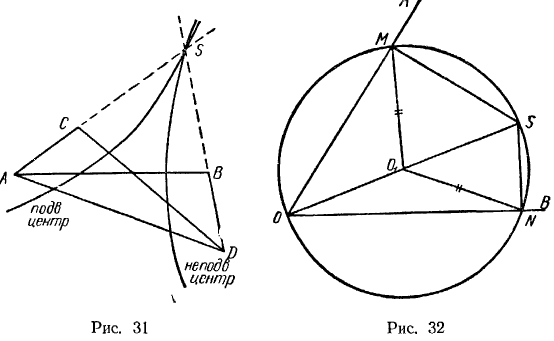
мгновенный центр вращения находится на продолжении прямой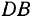 
. Обе упомянутые прямые пересекаются в некоторой точке 
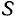, которая и будет мгновенным центром вращения стержня 
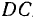. Из равенства 
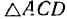и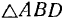 
непосредственно следует равенство:
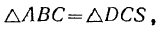
откуда получаем
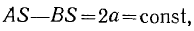
и, следовательно, геометрическим местом точек 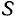будет гипербола, фокусы которой находятся в точках 
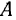и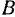 
. Эта кривая будет представлять собой неподвижную центроиду. Аналогично имеем
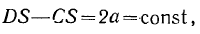
то есть геометрическим местом мгновенных центров по отношению к стержню 
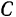будет гипербола с фокусами в точках и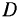 
. Непрерывное движение стержня можно теперь представить как качение без скольжения гиперболы, связанной со стержнем , по неподвижной гиперболе.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
