Оглавление:

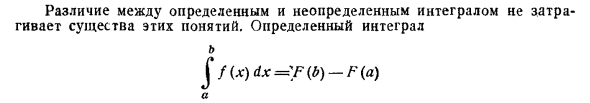

Определенный интеграл
- Определенный интеграл. Предположим, что f (x) — непрерывная функция, кривая y = f (x), ординаты x = a и x = b, а ось x имеет постоянную площадь. В пункте 148 гл. VI, F (hc) — это «интеграция» f (• )> R <) = f (x), F (x) = [f (x) dxt Площадь этой области F (b) -F (a). Поскольку не всегда возможно найти форму функции F (x)}, полезно предоставить выражение, представляющее область NlNPPl и явно не включающее (l :). Мы пишем: б (NlNPP1) = $ f (x) dx. но Правая часть этого уравнения может рассматриваться с двух точек зрения.
Здесь F (x) рассматривается, известна ли явная формула для этой разности, или этот символ указывает на область NXNPPV, определенную в пункте 161. б Дж / (х) дх но Это называется определенным интегралом. А и В называются их нижним и верхним пределами. / (Π) называется подынтегральным выражением, и, наконец, интервал (a, b) называется интервалом интегрирования (или областью). Определенный интеграл зависит только от формы a и b и функции / (). Это не функция х. С другой стороны, F (x) = jjf (x) dx иногда называют неопределенным интегралом от / ().
Это можно рассматривать как сокращение разности F (b) — • F (a). Людмила Фирмаль
| Дифференциалы | Площадь сектора круга. Круговые функции |
| Определенные интегралы и площади | Общие свойства определенного интеграла |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
Различие между определенными и неопределенными интегралами не влияет на сущность этих понятий. Определенный интеграл б J / (JC) DX =? F (b) -F (a) Является функцией от b и может рассматриваться как интеграл от функции / (£). С другой стороны, неопределенный интеграл F (x) всегда можно выразить через конкретный интеграл. X F (x) = F (a) + J f (t) dt но
Потому что одно является производным от другого. Интеграл X §F {i) dt a Является непрерывной функцией от x, поскольку имеет производную f (x). Поскольку функция непрерывна для всех положительных значений х, L Обсуждение в предыдущем параграфе включает в себя доказательство существования функции 1πх (см. §131).
Однако, когда рассматривается «неопределенный интеграл», это обычно означает определенную связь между двумя функциями. Людмила Фирмаль

