Определенный интеграл как предел интегральной суммы
Пусть функция  определена на отрезке
определена на отрезке  ,
, 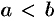 . Выполним следующие действия.
. Выполним следующие действия.
1. С помощью точек 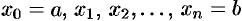
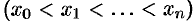 разобьем отрезок
разобьем отрезок  на
на  частичных отрезков
частичных отрезков 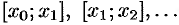
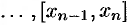 (см. рис. 166).
(см. рис. 166).
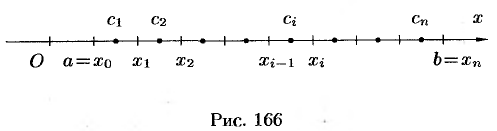
2. В каждом частичном отрезке 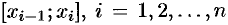 выберем произвольную точку
выберем произвольную точку 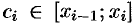 и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину 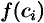 .
.
3. Умножим найденное значение функции 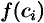 на длину
на длину 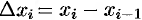 соответствующего частичного отрезка:
соответствующего частичного отрезка: 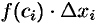 .
.
4. Составим сумму 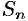 всех таких произведений:
всех таких произведений:
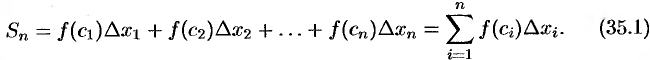
Сумма вида (35.1) называется интегральной суммой функции  на отрезке
на отрезке  . Обозначим через
. Обозначим через 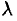 длину наибольшего частичного отрезка:
длину наибольшего частичного отрезка: 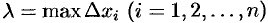 .
.
5. Найдем предел интегральной суммы (35.1), когда 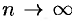 так, что
так, что 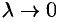 .
.
Если при этом интегральная сумма 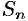 имеет предел
имеет предел 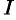 , который не зависит ни от способа разбиения отрезка
, который не зависит ни от способа разбиения отрезка  на частичные отрезки, ни от выбора точек в них, то число
на частичные отрезки, ни от выбора точек в них, то число 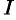 называется определенным интегралом от функции
называется определенным интегралом от функции  на отрезке
на отрезке  и обозначается
и обозначается 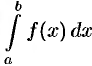 . Таким образом,
. Таким образом,
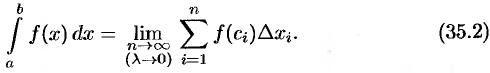
Числа 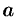 и
и 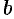 называются соответственно нижним и верхним; пределами интегрирования,
называются соответственно нижним и верхним; пределами интегрирования,  — подынтегральной функцией,
— подынтегральной функцией, 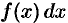 — подынтегральным выражением,
— подынтегральным выражением,  — переменной интегрирования, отрезок
— переменной интегрирования, отрезок  — областью (отрезком) интегрирования.
— областью (отрезком) интегрирования.
Функция  , для которой на отрезке
, для которой на отрезке  существует определенный интеграл
существует определенный интеграл 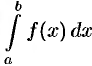 , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Сформулируем теперь теорему существования определенного интеграла.
Теорема 35.1 (Коши). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл
, то определенный интеграл 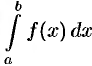 существует.
существует.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).
1. Определенный интеграл не зависит от обозначения переменной интегрирования:
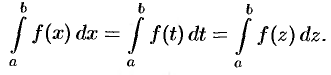
Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
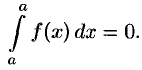
3. Для любого действительного числа 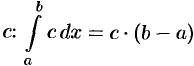 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интегрирование дифференциального бинома |
| «Берущиеся» и «Неберущиеся» интегралы |
| Геометрический и физический смысл определенного интеграла |
| Основные свойства определенного интеграла |

