Оглавление:
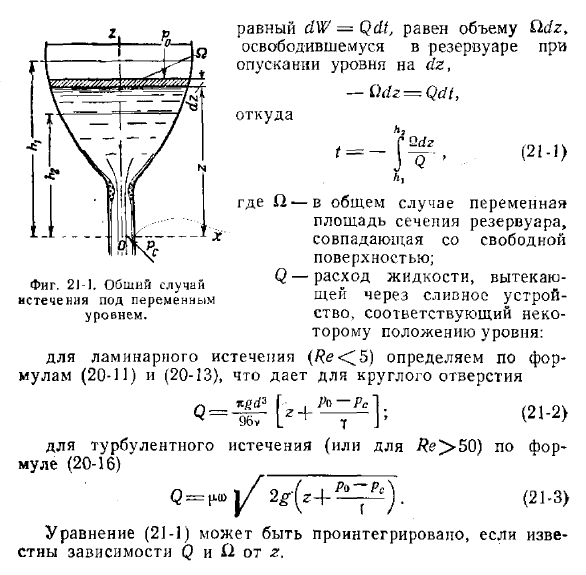
Определение времени опорожнения резервуара. Общий случай
Определение времени опорожнения резервуара. Общий случай. При изучении потока жидкости через отверстия и сопла на переменных уровнях необходимо исходить из уравнения Бернулли с нестационарным движением. Однако влияние инерционного давления обычно не важно и может быть проигнорировано.
Движение жидкости в рассматриваемом случае является неустановившимся, т. к. напор изменяется с течением времени, а, следовательно, меняется и расход вытекающей жидкости. Людмила Фирмаль
- Используйте непрерывную формулу для определения времени опорожнения резервуара (Рисунок 21-1). Это позволяет количеству жидкости, вытекшей из резервуара с течением времени (истечение жидкости из резервуара на 364 переменных уровнях, равный объему Ки, выпущенному в бак при снижении уровня на кг), -Oig = C1sN.
- Откуда в общем случае переменная площадь поперечного сечения резервуара. Совпадающая со свободной поверхностью, скорость потока жидкости, протекающей через дренажное устройство, соответствующая определенному положению уровня.
Смысл этой гипотезы состоит в том, что если уровень жидкости в сосуде меняется медленно, то истечение жидкости в течение каждого интервала времени можно считать установившимся и пользоваться формулой, полученной для расхода жидкости при постоянном напоре. Людмила Фирмаль
- Для ламинарного истечения (/ ^ <5), определяемого уравнениями (20-11) и (20-13), дается круглое отверстие. <2> −2> В случае турбулентного оттока (или если #e> 50), согласно уравнению * (20-16) 0 = ^ [/ Γ2 (21-3) Если вы знаете зависимость @ и 12 от r, вы можете интегрировать уравнение (21-1)
Смотрите также:
Возможно эти страницы вам будут полезны:
- Истечение жидкости через распылители.
- Траектория свободной струи.
- Определение времени истечения жидкости из резервуара с постоянным поперечным сечением по высоте.
- Определение времени истечения жидкости из резервуара с переменным поперечным сечением
