Оглавление:
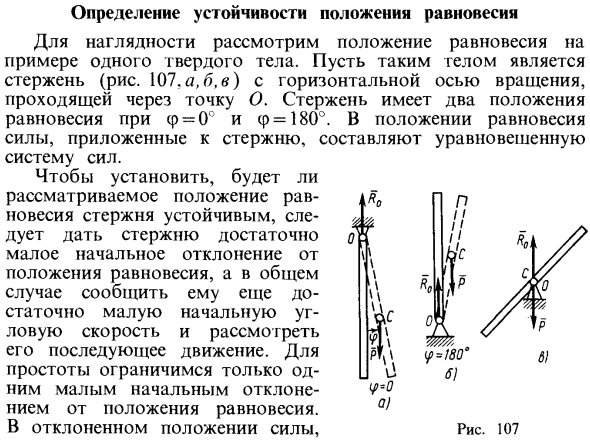



Определение устойчивости положения равновесия
- Для ясности рассмотрим равновесие одного твердого примера. Таким объектом является стержень, ось вращения которого проходит через точку О (рис. 107, а, б, в). Штанга имеет два положения равновесия при 0 и m] 2> 0 можно выбрать для достаточно малого £> 0, равновесие системы называется устойчивым. q ”| <t | t, | q ° | <m] Если 2, все обобщенные координаты подчиняются условию | <y ((z) | <£.
Это предположение довольно хорошо соответствует действительности для элементарной трубки тока, но его применяют и для труб конечных размеров, используя средние величины по сечениям трубы. Людмила Фирмаль
Таким образом, по словам Ляпунова, достаточно малая область флуктуаций начального значения обобщенных координат вблизи положения равновесия и значения обобщенных координат при последующих движениях системы ограничены определенной окрестностью вблизи положения равновесия. Положение равновесия считается стабильным, если можно указать область начальной скорости обобщения.
- Понятно, что область q ° и начальное значение q °, определяемые положительным числом и m] 2, зависят от выбранной окрестности E, то есть числа e. Есть ли области для этих q начальных значений? И q ° не должно соответствовать m) 2 = 0 и m) 2 = 0. Другими словами, поддерживается только само положение равновесия. В этом случае <7? = 0 и <7? = 0 В положении равновесия механической системы каждая обобщенная сила O равна нулю.
Уравнения Лагранжа для обобщенных координат являются обыкновенными дифференциальными уравнениями второго порядка, как и дифференциальные уравнения движения точки в декартовых координатах. Людмила Фирмаль
Для потенциальных силовых полей обобщенная сила рассчитывается через потенциальную энергию по следующей формуле: Qi ^ -dllldqi, i = 1, 2, …, n Следовательно, в равновесном положении dnjdq ^ Q, следовательно, потенциальная энергия в этом случае может достигать своего предельного значения.
Смотрите также:
Задачи по теоретической механике
| Канонические уравнения | Теорема Лагранжа—Дирихле |
| Устойчивость положения равновесия | Колебания системы с одной степенью свободы |

