Оглавление:
Определение ускорения точки при задании ее движения естественным способом
Если движение точки задано естественным способом, то ускорение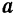 
точки раскладывается на составляющие, направленные по так называемым естественным осям координат. Такое разложение удобно и потому, что эти составляющие характеризуют, как мы увидим дальше, разные стороны изменения вектора скорости.
Введем предварительно некоторые понятия.
Плоскость, проходящая через касательную к кривой в данной ее точке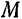 
и другую, бесконечно близкую к ней, точку кривой, называется соприкасающейся плоскостью в точке .
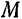Ясно, что в случае плоской кривой соприкасающейся плоскостью для всех ее точек является плоскость, в которой лежит сама кривая.
Плоскость, перпендикулярная к касательной, называется нормальной плоскостью (рис.111). Любая
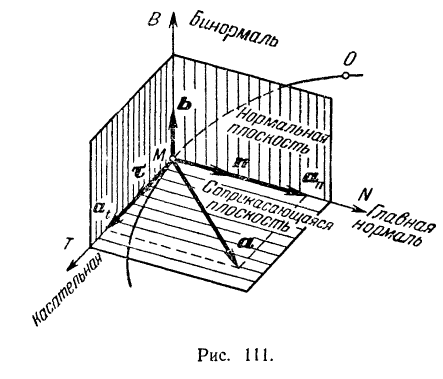
прямая, проведенная в нормальной плоскости через точку 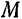, будет перпендикулярна к касательной и является нормалью к кривой.
Нормаль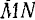 
, лежащая в соприкасающейся плоскости, называется главной нормалью, а нормаль 
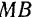, перпендикулярная к главной нормали, называется бинормалью.
Естественными осями координат называется совокупность трех взаимно перпендикулярных осей, начало которых совпадает в каждый момент с положением движущейся точки 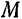(рис. 111). Одна из этих осей (
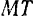) направлена по касательной к траектории точки в сторону положительного отсчета расстояний 
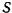, другая (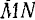) направлена по главной нормали в сторону вогнутости траектории и третья (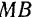) направлена по бинормали так, чтобы она образовывала с первыми двумя осями правую систему координат.
Отложим по введенным координатным осям (рис. 111) единичные векторы (орты): касательной —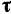 
, главной нормали — 
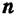бинормали — 
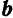. Вектор 
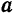ускорения разложим на составляющие по естественным осям координат. Обозначая через 
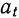— проекцию вектора а на касательную, через 
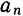— его проекцию на главную нормаль и через 
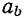— его проекцию на бинормаль, можно записать, что
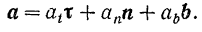
Так как скорость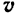 
точки всегда направлена по касательной к траектории, то 
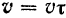. Правая часть этого равенства представляет собой, 0 вообще говоря, произведение двух переменных: 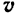— величины скорости (ее проекции на касательную) и 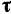— орта касательной.
По формуле (59) для ускорения точки будем иметь:
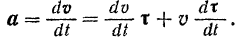
Найдем сначала модуль производной по времени от орта касательной
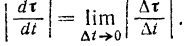
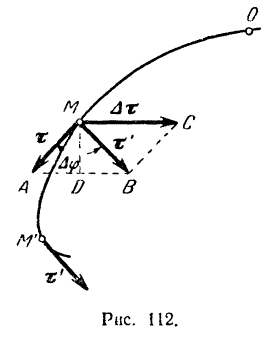
Определим для этого приращение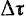 
орта касательной при переходе точки за промежуток времени 
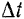из положения 
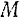в положение 
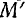(рис. 112). Проведем из точки 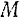вектор 
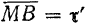и построим параллелограмм 
.
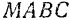Из него находим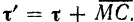 
Следовательно,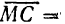 
.
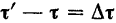Обозначим через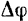 
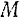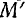так называемый угол смежности, т. е. угол между направлениями касательных в точках и кривой.
Треугольник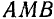 
— равнобедренный, так как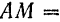 
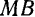. Высота этого треугольника является биссектрисой угла 
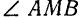и медианой стороны 
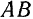. Следовательно:
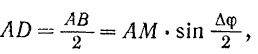
откуда
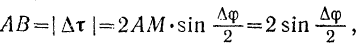
так как
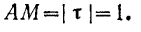
Подставляя найденное значение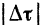 
в равенство (III) и преобразовывая правую часть этого равенства так, чтобы получить ее в виде произведения величин, пределы которых можно вычислить, находим:
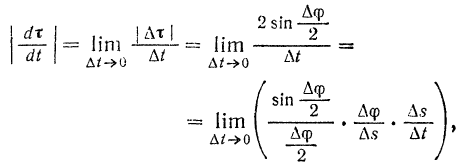
где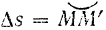 
— приращение дуговой координаты 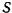точки за промежуток времени 
.
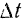Если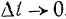 
, то 
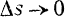и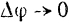 
. Следовательно, равенство (IV) можно переписать так:
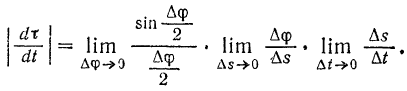
Стоящие в правой части последнего равенства пределы легко находятся:
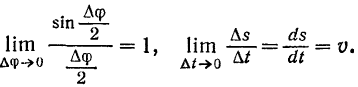
Как известно из курса высшей математики, предел отношения угла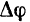 
смежности к длине 
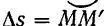соответствующей ему дуги, когда длина этой дуги стремится к нулю, равен кривизне линии в данной точке 
.
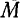Кривизна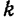 
линии в точке 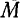является величиной, обратной радиусу 
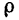кривизны в этой точке. Следовательно,
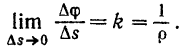
Подставляя найденные значения соответствующих пределов в правую часть равенства (V), получим
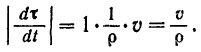
Для того чтобы определить направление вектора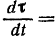 
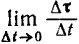найдем предельное значение угла между векторами 
и 
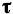при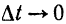 
. Из рис. 112 видно, что
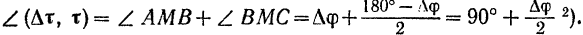
Так как при 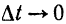угол смежности 
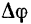также стремится к нулю, то
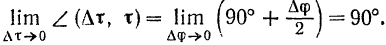
Вектор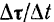 
лежит в плоскости параллелограмма 
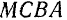(рис. 112). В пределе, при неограниченном приближении точки 
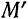к точке 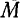, т. е. при 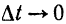, плоскость этого параллелограмма будет совпадать с соприкасающейся плоскостью. Следовательно, вектор 
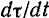лежит в соприкасающейся плоскости, и, как видно из рис. 112, направлен в сторону вогнутости кривой. Кроме того, по доказанному выше он перпендикулярен к вектору 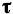. Из всего сказанного следует, что направление вектора 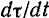совпадает с направлением орта 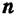главной нормали к траектории в точке 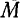. Учитывая найденное ранее (VI) значение его модуля, будем иметь:
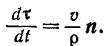
Подставляя это значение в выражение (II), получаем
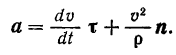
Сравнивая равенства (I) и (VIII), находим:
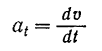
— проекция ускорения точки на касательную равна первой производной от численного значения ее скорости по времени;
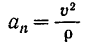
— проекция ускорения точки на главную нормаль (модуль нормального ускорения) равна квадрату ее скорости, деленному на радиус кривизны траектории в соответствующей ее точке;
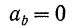
— проекция ускорения точки на бинормаль равна нулю.
Отсюда следует, что ускорение а точки лежит в соприкасающейся плоскости траектории и его всегда можно разложить на две составляющие, направленные по осям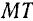 
и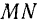 
:
составляющая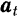 
ускорения точки, направленная по касательной к траектории, называется касательным или тангенциальным ускорением;
составляющая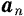 
ускорения точки, направленная по главной нормали к траектории, называется нормальным ускорением.
Проекция ускорения точки на главную нормаль 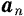всегда положительна, и потому нормальное ускорение 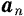всегда направлено в сторону вогнутости траектории.
Касательное же ускорение направлено в сторону положительного отсчета расстояний, если
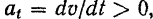
и в противоположную сторону, если
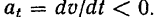
Очевидно, что точка движется ускоренно, если проекции скорости
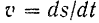
и касательного ускорения
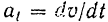
имеют одинаковые знаки, и замедленно, если эти проекции имеют разные знаки.
При задании движения точки естественным способом нам известны как траектория точки (а следовательно, и ее радиус кривизны в любой точке), так и уравнение движения точки по данной траектории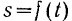 
. Зная это, мы можем определить скорость точки (по формуле (67)), а затем касательное и нормальное ускорения точки (по формулам (68) и (69)).
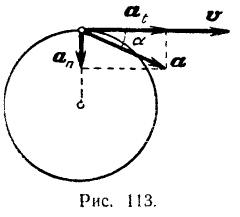
Зная проекции вектора а на две взаимно перпендикулярные оси (касательную и нормаль к данной точке траектории), легко найти (рис. 113) как модуль, так и направление самого вектора ускорения точки:
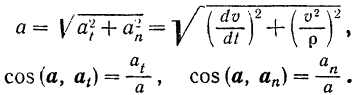
Пример задачи:
Точка движется по окружности радиуса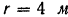 
по закону 
(
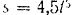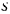— в метрах, 
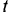— в секундах). Найти модуль ускорения точки и угол 
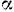между ускорением и скоростью в тот момент 
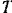, когда скорость точки равна 6 м/сек.
Решение:
Модуль скорости точки
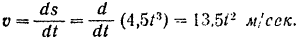
По условию задачи при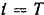 
скорость точки 
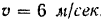. Подставляя эти данные в выражение скорости, находим 
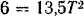, откуда
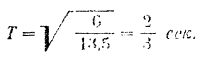
Касательное ускорение точки
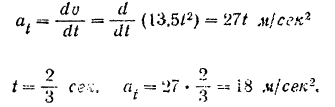
Нормальное ускорение точки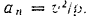 
. Подставляя выражение 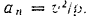и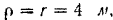 
, находим 
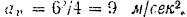. Ускорение (полное) точки
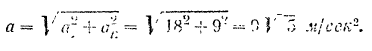
Угол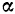 
(рис. 113) между ускорением 
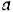и скоростью 
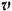точка определится из формулы
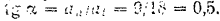
Отсюда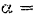 
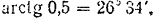
Пример задачи:
Точка совершает движение по винтовой линии согласно уравнениям
(
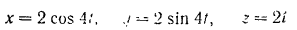
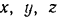— в метрах, 
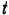— в секундах). Определить численные значения скорости и ускорения точки, а также радиус кривизны ее траектории.
Решение:
Проекции скорости на координатные оси:
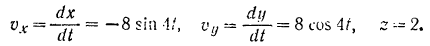
Модуль скорости
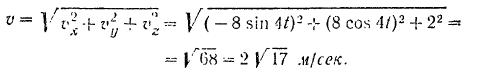
Проекции ускорения на координатные оси:
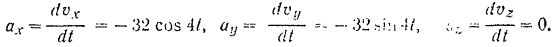
Модуль ускорения
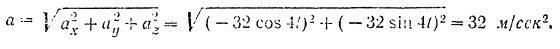
Так как модуль v скорости — величина постоянная, то касательное ускорение
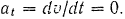
Таким образом, ускорение а точки состоит только из се нормального ускорения
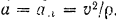
Отсюда находим радиус кривизны траектории
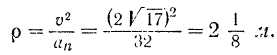
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
