Оглавление:




Определение точки перегиба. Необходимое условие перегиба
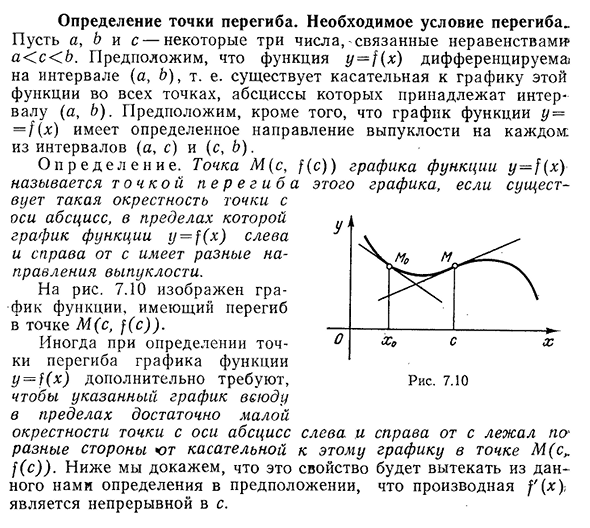
- Определение точки перегиба. Предположим, что функция g / = / (x) дифференцируема по интервалу (a, B), то есть на графике этой функции имеются касательные во всех точках, в которых абсцессы принадлежат интервалу (a, B). кроме того, граф функции y==f (x) имеет направление выпуклости, которая находится в каждом из них. Точка M (C, f (C)) графа функции y—f (x) называется точкой t n E R e E g,
где b a V-окрестность точки C на оси абсцисс, а граф функции y=f (x) слева и справа от C находится в разных направлениях. Для риса. 7.10 точки M (C, f (c)) показывают график функции с перегибом. В некоторых случаях при определении точки перегиба графа функция y=f (x) дополнительно требует, чтобы указанный граф
находился в любом месте достаточно малого графа. Если этот граф существует- Людмила Фирмаль
Окрестность C в точках левого и правого абсцисс C противоположна касательной этого графа в точке M(C » f (c)). В следующем, это свойство производной функции f'(x) является p.274 в предположении, что она непрерывна в главе 7, мы докажем, что это следует из нашего определения. Рассмотрим график функции Следующие две леммы доказаны. Л Е М М А1. Функция y=f(x) имеет производную f'(x) в любом месте окрестности d точки C, и эта производная непрерывна в точке C. Если граф y=f(x) находится в интервале (C,C+6), он
ориентирован к вершине и касается графа, нарисованного M (C, f (c)). Д О К а з а т е л ь с Т В О. через каждую точку графа функции y=f(x) MP(xn, f (xn)) проведем касательную к этому графу, то есть Прямую линию * * Используйте уравнение линии, которая проходит через заданную точку (C n, 1 (Xn)) и имеет текущий угловой коэффициент*вертикальная ось этой линии показывает Yn. До=/(л ПРОМАЛЬП)+/[л. с.) (х х»). По условию граф функции y=f (x) имеет
- выпуклую форму, направленную вниз[вверх]для интервала (C, C+6), тогда интервал любого числа n и любой неподвижной точки x (C, C+6) *(из условия непрерывности f'{x) (далее f (x)) точка C и определение,->STO (/(x) точка C и определение [вверх]=== = = = = = = = = = = = = = = = = ниже приведен список функций, которые используются в программе. Из существования последнего предела по неравенству) (и теоремы 3.13 в Главе 1 3.13 мы получаем, что f(x) — f(c) — f'(c) (x-c)^O[CO]. Если
обозначить через Y текущую ординату касательной (7.5), проходящей через точку M[C, f (c)), то последнее неравенство можно переписать как f(x)-Y>0[<0]. . Итак, используя теорему 3.13 до пределов) (n — >OO), получаем f (x)-Y+0[CO]для любой неподвижной точки x из интервала (C, C+0), а Y рисуется через точку M (C, f (c)). Леммы доказаны. Аналогично,
Лемма 1 формулируется и доказывается для случаев, когда граф функции имеет определенное направление выпуклости, лежащее на интервале (C—6, C), а не на интервале (C+6).§3. Точка Людмила Фирмаль
перегиба 27С Л ем м А2. И если граф функции y=f (x) достаточно мал из 6 точек левой и правой точек этого графа, которые имеют разные стороны от касательных, проведенных через точку M (C, f (c)), то граф будет одинаковым. Для этой леммы вам нужно выбрать b>0-с каждым интервалом(C-b, C). График функции (C, c+b) y=f (x) имеет определенное направление выпуклости (это направление отличается интервалами (C—b, C) и (C, C+b)). Затем остается применить лемму 2 к функциям y=f (x) для каждого интервала (C—b, C) и (C, C+b), чтобы доказать лемму 2. Лемма 2 позволяет установить необходимые условия для перегиба графа функции y=f (x), которая дважды
выделяется в заданных точках. 7.7(л о В Е П Е ги Б А Ф К А Д В Д в р О С Д и Ф Е Р Е Н Т Р У М О й ф у Н К т и о н). Если функция y=f (x) имеет квадратичную производную в C, а граф этой функции имеет перегиб в m (C, 1 (c)), то f2>(c)=O. D o K a z a t e l s T V o. как упоминалось выше, Y-текущая ордината касательной Y=f (c)+f'(c) (x—C), проходящей через точки графа M (C, f (C)). Рассмотрим, что F (x)=f (x)—Y=f (x)—f (x)—f (c)—f (c) (C) (x—C) равно разности между f (x) и линейной функцией f(C)+/'(C) (x-C). Эта функция F (x), так же как и функция f (x), имеет вторую производную в точке C (следовательно, имеет первую производную в некоторой окрестности C, Эта первая производная
благодаря Лемме 2 в точке C, в Малой окрестности точки C, график функции y=f (x) находится слева и справа от Малой окрестности точки C). Таким образом, функция F (x) не может иметь локальных экстремумов в точке C. Где f (2) (c)+=0. Тогда f/(x)=f(x)=f (c)-f'(c), F^(x)=ft2) (x), поэтому выполняется условие f'(c)=0″f (2) (c)=+0, а функция F (x) по теореме 7.2 имеет локальное экстремальное значение в C. теорема доказана. Дело в том, что исчезновение второй производной является лишь необходимым условием для преобразования графа
двудифференцируемой функции, например:■276 Глава 7. Рассмотрим график функции График функции Z/=Х4. В этой функции вторая производная y » =12×2 исчезает в точке x=0, но ее график не имеет точки перегиба в точке M(0, 0). Благодаря теореме 7.7, чтобы найти все точки перегиба графа двудифференцируемой функции y=f (x), необходимо учесть все корни уравнения f<2) (x)=0. Поскольку эквивалентность второй производной нулю является лишь необходимым условием для перегиба, необходимо дополнительно исследовать проблему наличия перегиба в каждой точке f (2) (x)=0. Для таких исследований необходимо установить достаточные условия интонации, к чему мы и приступим.
Смотрите также:
Методическое пособие по математическому анализу

