Определение скорости точки при задании ее движения естественным способом
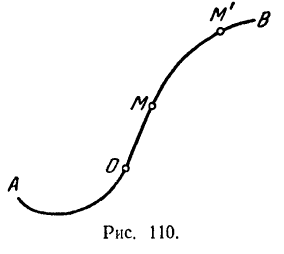
При естественном способе задания движения точки нам должны быть известны ее траектория 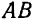 (рис. 110) и уравнение движения по этой траектории
(рис. 110) и уравнение движения по этой траектории 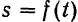 , где
, где 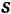 — дуговая координата точки. Пусть в момент
— дуговая координата точки. Пусть в момент 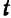 точка находилась на траектории в положении
точка находилась на траектории в положении 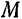 и за промежуток времени
и за промежуток времени 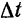 перешла в положение
перешла в положение 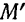 , переместившись по траектории на дугу
, переместившись по траектории на дугу
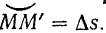
Средняя величина скорости точки за какой-либо промежуток времени будет равна:
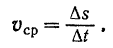
Предел этого отношения при 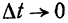 будет численным значением скорости в соответствующий момент времени
будет численным значением скорости в соответствующий момент времени 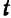 :
:
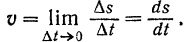
Если точка 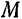 движется в сторону положительного отсчета расстояний, то приращение
движется в сторону положительного отсчета расстояний, то приращение 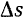 ее расстояния от начала отсчета будет положительным и производная
ее расстояния от начала отсчета будет положительным и производная 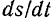 будет также положительной. Если же точка
будет также положительной. Если же точка 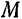 движется в сторону отрицательного отсчета расстояний, то приращение
движется в сторону отрицательного отсчета расстояний, то приращение 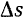 и производная
и производная 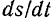 будут отрицательными.
будут отрицательными.
Следовательно, производная 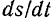 дает так называемое алгебраическое значение скорости, которым определяется не только модуль скорости точки, но и направление ее движения по траектории.
дает так называемое алгебраическое значение скорости, которым определяется не только модуль скорости точки, но и направление ее движения по траектории.
Если промежуток времени 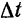 , следующий за моментом времени
, следующий за моментом времени 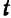 , взят настолько малым, что направление движения точки в течение этого промежутка можно считать неизменяющимся, то абсолютное значение приращения
, взят настолько малым, что направление движения точки в течение этого промежутка можно считать неизменяющимся, то абсолютное значение приращения 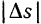 расстояния точки от начала отсчета равно приращению
расстояния точки от начала отсчета равно приращению 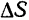 пути, пройденного точкой за тот же промежуток времени
пути, пройденного точкой за тот же промежуток времени 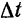 . Путь
. Путь 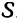 , проходимый точкой, также, очевидно, есть некоторая функция времени.
, проходимый точкой, также, очевидно, есть некоторая функция времени.
Приращение же пути, конечно, всегда положительно. Тогда модуль скорости точки
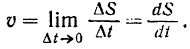
В целях упрощения записи обычно не делают различия в обозначениях модуля вектора и его алгебраического значения.
Соединяя в одно равенства (1) и (11) и учитывая, что модуль вектора есть всегда неотрицательная величина, можно записать:
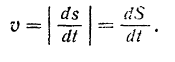
Модуль скорости точки ровен модулю производной от ее дуговой координаты по времени или производной от пройденного ею пути по времени.
Направлена скорость 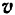 точки всегда, как было сказано в § 44, по касательной к траектории точки.
точки всегда, как было сказано в § 44, по касательной к траектории точки.
Нужно заметить, что при криволинейном движении точки величина ее средней скорости 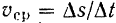 (определяемая из движения точки по дуге
(определяемая из движения точки по дуге 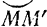 траектории) не равна модулю
траектории) не равна модулю 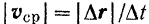 вектора ее средней скорости (определяемой из движения точки по хорде
вектора ее средней скорости (определяемой из движения точки по хорде 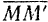 ). Но в пределе при
). Но в пределе при 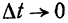 модуль скорости точки в данный момент, определяемый по формулам
модуль скорости точки в данный момент, определяемый по формулам
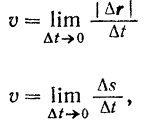
будет иметь одинаковое значение, так как
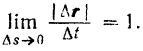
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

