Оглавление:
Определение скорости и ускорения точки при задании ее движения координатным способом
Пусть точка движется относительно некоторой системы координат 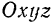 согласно заданным уравнениям;
согласно заданным уравнениям;
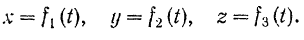
Приняв за начало радиуса-вектора движущейся точки начало данной системы координат, можно написать в соответствии с формулой (55)
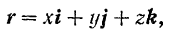
где орты «неподвижных» координатных осей 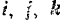 постоянны как по модулю, так и по направлению.
постоянны как по модулю, так и по направлению.
Из курса высшей математики известно, что правила дифференцирования векторных функций аналогичны правилам дифференцирования скалярных функций. В частности, производная суммы равна сумме производных и производная произведения постоянного вектора на скалярную функцию раина произведению этого вектора на производную от скалярной функции.
Вспоминая формулу (57), будем иметь:
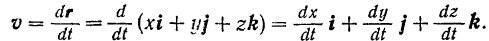
С другой стороны, вектор v, как и всякий вектор, можно выразить через его проекции на координатные оси
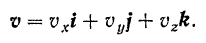
Сравнивая равенства (I) и (II), находим:
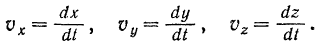
Проекция скорости точки на какую-либо координатную ось равна производной от соответствующей координаты точки по времени.
Если проекции вектора на оси координат известны, то легко определяются и модуль и направление вектора. Модуль вектора скорости
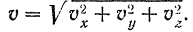
Его направляющие косинусы:
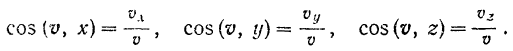
Аналогично определяется и ускорение точки. Из формулы (59) следует:
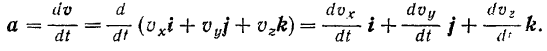
Отсюда находим выражения для проекций ускорения на оси координат:
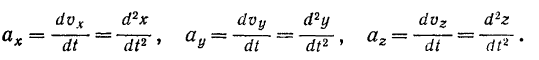
Проекция ускорения точки на какую-либо координатную ось равна первой производной по времени от проекции ее скорости на эту ось или второй производной от соответствующей координаты точки по времени.
Модуль вектора ускорения
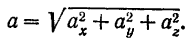
Его направляющие косинусы:
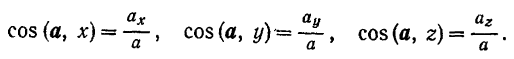
Если движение точки происходит в одной плоскости, то достаточно двух уравнений 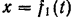 и
и 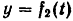 , и в соответствующих формулах отпадают проекции скорости и ускорения точки на ось
, и в соответствующих формулах отпадают проекции скорости и ускорения точки на ось 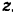 .
.
Пример задачи:
Движение снаряда задано уравнениями
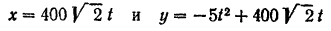
(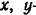 — в метрах,
— в метрах, 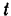 — в секундах). Определить: 1) уравнение траектории, 2) высоту
— в секундах). Определить: 1) уравнение траектории, 2) высоту 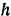 и дальность
и дальность 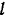 полета, 3) скорость
полета, 3) скорость 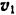 в наивысшей точке траектории и скорость
в наивысшей точке траектории и скорость 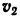 в тот момент, когда снаряд упадет на землю.
в тот момент, когда снаряд упадет на землю.
Решение:
1) для определения траектории движения снаряда исключаем время из уравнений его движения:
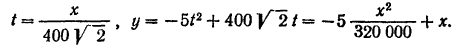
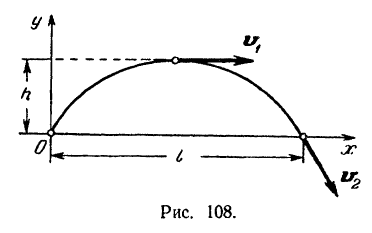
Траекторией снаряда служит парабола (рис. 108), определяемая уравнением
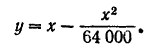
2) Траектория снаряда пересекает ось 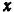 в двух точках, для которых ордината
в двух точках, для которых ордината 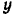 равна нулю. Подставляя это значение
равна нулю. Подставляя это значение 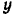 в уравнение траектории, находим абсциссы точек пересечения:
в уравнение траектории, находим абсциссы точек пересечения:
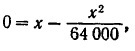
откуда
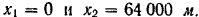
Ясно, что дальность полета снаряда
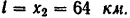
Для определения максимальной высоты 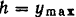 подъема снаряда можно было бы воспользоваться общим приемом определения максимума функции
подъема снаряда можно было бы воспользоваться общим приемом определения максимума функции 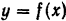 , но в данном случае, ввиду симметричности кривой, искомую высоту легко найти, подставив в уравнение траектории
, но в данном случае, ввиду симметричности кривой, искомую высоту легко найти, подставив в уравнение траектории
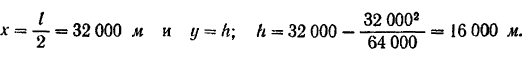
3) Проекции скорости снаряда на координатные оси определяются по формулам (60):
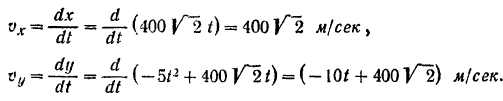
Как видим, проекция скорости снаряда на ось 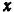 постоянна, проекция же этой скорости на ось
постоянна, проекция же этой скорости на ось 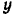 зависит от времени движения снаряда.
зависит от времени движения снаряда.
В наивысшей точке траектории скорость снаряда параллельна оси 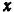 . Следовательно,
. Следовательно,
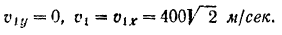
Для определения скорости 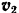 снаряда в момент
снаряда в момент 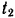 падения его на землю необходимо найти время полета снаряда. Для этого подставим в уравнение движения
падения его на землю необходимо найти время полета снаряда. Для этого подставим в уравнение движения 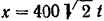 значения
значения 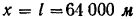 и
и 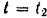 . Будем иметь:
. Будем иметь:

Подставив найденное значение времени 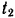 полета снаряда в выражения для проекций скорости снаряда, находим:
полета снаряда в выражения для проекций скорости снаряда, находим:
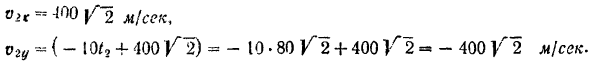
Модуль искомой скорости снаряда
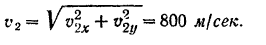
Направление этой скорости определяется из формулы (62):
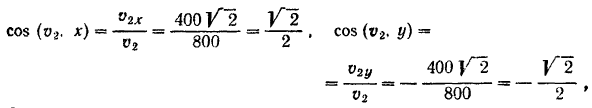
откуда
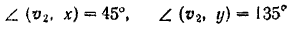
Пример задачи:
Написать уравнения движения в прямоугольных координатах и определить скорость и ускорение конца 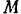 кривошипа
кривошипа 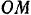 , вращающегося вокруг неподвижного центра
, вращающегося вокруг неподвижного центра 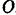 . Длина кривошипа
. Длина кривошипа 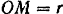 . Угол поворота кривошипа относительно горизонтальной оси изменяется по закону
. Угол поворота кривошипа относительно горизонтальной оси изменяется по закону 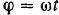 .
.
Решение:
Возьмем систему координат 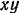 с началом в точке
с началом в точке 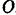 . Координаты точки
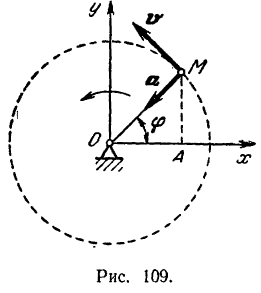
. Координаты точки 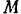 в этой системе (рис. 109):
в этой системе (рис. 109):
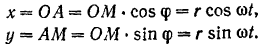
Проекции скорости точки  на координатные оси:
на координатные оси:
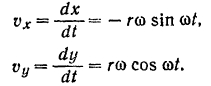
Модуль скорости
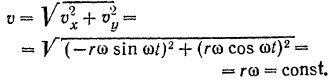
Скорость точки  по модулю постоянна. Направление скорости этой точки можно определить из формул:
по модулю постоянна. Направление скорости этой точки можно определить из формул:
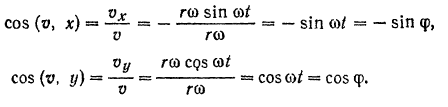
Проекции ускорения точки 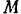 на координатные оси:
на координатные оси:
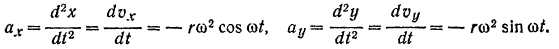
Модуль ускорения
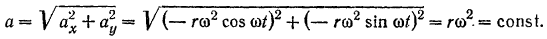
Ускорение точки 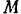 по модулю также постоянно. Оно не равно нулю, несмотря на то что скорость этой точки по модулю постоянна. Вследствие криволинейности траектории точки все время изменяется направление скорости. Направление ускорения точки
по модулю также постоянно. Оно не равно нулю, несмотря на то что скорость этой точки по модулю постоянна. Вследствие криволинейности траектории точки все время изменяется направление скорости. Направление ускорения точки 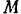 можно определить из формул (65):
можно определить из формул (65):
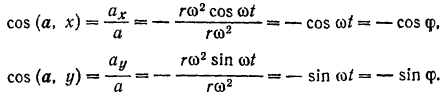
Нетрудно убедиться, что при равномерном движении точки 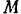 по окружности ее ускорение а направлено к центру окружности.
по окружности ее ускорение а направлено к центру окружности.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

