Оглавление:
























Определение скоростей и ускорений точек твердого тела, вращающегося вокруг неподвижной точки
- Определение скорости и ускорения точки в твердом теле, вращающемся вокруг неподвижной точки Выберите фиксированную систему координат xyz с фиксированной точкой начала координат 0 и осями в той же фиксированной системе координат X \ Y \ 2 \и жестко соедините жесткое тело. Линия ON, которая является пересечением неподвижной плоскости xy и движущейся плоскости xyy, называется линией узла.
Угол прецессии 6 измеряется от неподвижной оси x до линии узла ON и считается положительным, если вращение от оси z происходит против часовой стрелки(рис.7.1).. Угол чистого или соответствующего поворота
Угол прецессии находится в неподвижной плоскости xy Людмила Фирмаль
= /、(0、* = / *(/)。0 = / 3(0-0 *) Рисунок 7.1. от оси z до оси z{и отсчет от линии узла на、 И А К О К сои, и вах скорость и ускорение точки М ых з {): 1) определяет производную угла Эйлера по времени. 2) Найти проекцию угловой скорости на оси неподвижной и подвижной системы координат 3) вычислить мгновенную угловую скорость. 4) определите положение мгновенной оси. 5)
Создайте уравнения неподвижных и подвижных осей. Ж) найти мгновенное угловое ускорение как скорость конца вектора со, либо через проекцию углового ускорения на движущуюся и неподвижную оси. 7) определите величину точки G и скорость направления. 8) найти точку M, проекцию вращательного ускорения и кормового ускорения, или точку M ускорения на неподвижной оси с осью координатного движения. 0)
- вычислить величину и направление ускорения точки A1. В., он показывает положение оси вращения и скорость точки M. It необходимо определить мгновенную угловую скорость, мгновенное угловое ускорение, неподвижную и движущуюся скорость, ускорение и разгон любой точки твердого тела. 1) Выберите фиксированную и перемещенную систему координат. 2) Найти мгновенную угловую скорость твердого тела. 3) определите нужную скорость движения твердых точек. 4) найти мгновенное угловое ускорение твердого тела как скорость вектора края мгновенной угловой скорости. 5)
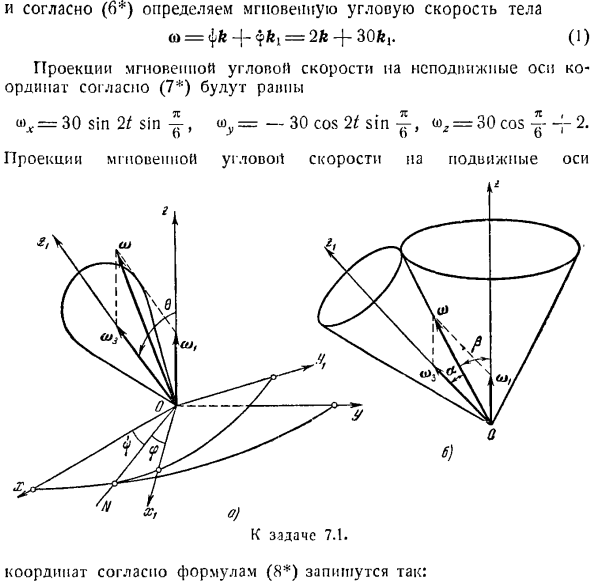
рассчитайте вращение точек твердого тела и самое сильное ускорение, и даже их ускорение. ( > ) Идентифицирует движимые и недвижимые экспиды. Задача 7.1.Твердое тело вращается вокруг неподвижной точки в соответствии с уравнением. ТЖ> = 2Д <Р = 30/, 0 = |-、 Где угол (рисунок I) — радианы, а время измеряется в секундах. Определяет скорость (xlt y z {) >точки в объекте M с мгновенной угловой скоростью объекта, уравнение мгновенной оси, неподвижного и подвижного осеподобного тела и координаты движущейся системы координат, которые неподвижно связаны с объектом. ХХ = 2 см м}-3 см,= 5 см. Решение.
Существует 2 системы координат с фиксированной точкой O в качестве начала координат. Людмила Фирмаль
Перемещение јсјбыл Дж/ журн является фиксированной, подключенный твердых и ж является фиксированной фьюзинг системы. Найти производную по времени от угла Эйлера. f= 2、$ = 30、0 = 0、 (6) определите мгновенную угловую скорость тела согласно = + = 2К + 30fe,. (1) (7) проекция мгновенной угловой скорости на неподвижную естественную по координатам путем царапания ДС = 30 грех 21 грех со ^ == = = −30 потому что 21 грех <ОЗ = 30cos — Дж-2.
Проекция мгновенной угловой скорости движущейся оси Я… Координаты по формуле (8) записываются следующим образом: К задаче 7.1. towl = 2 грех ^ грех 30/, СЧЛ = Р 2 грех, потому что 30/, » к, = 2, потому что + 30. Величина мгновенной угловой скорости определяется по формуле (9). У)= Vф + 2ph6 потому что о = =] / «4 + 900 + 2.301 / 3 ^ 1 ^ 008 ^ 31.8 секунды. Проекция м-скорости эструса на движущуюся ось определяется по формуле (5*). VXL по = ioflZi-<О2 | Г, = 5 соѕ 30 / — (Дж / 3 + 30)3 = 5 потому что 30 /-95.19、^ = »> / 1 * 1-(/ 3 + 20)2 −5 грех 30 / = 68.46-5 грех 30/, витл = 4 — = 3 грех 30 /-2 соѕ 30 /. Скорость точки автофокусировки прогнозируется по формуле: ® = + + = Косинус 30 * −95.19),+ +(63.46-5 sin 300] \ — g(3 sin 30 ′ −2 cos 300 K
Мгновенное уравнение оси фиксированной системы координат по (10) имеет вид: _ = I_ =(2) 15 грех это-Локос 21 28 * к) Уравнение мгновенной оси в системе перемещения оси на основе (и*) имеет вид、 _ £Призраки _ У1 _ З \ / М \ грех 30 * ~ ~, потому что 30 *-31.73 * к ’ Выведите из этих уравнений уравнение неподвижного и движущегося присоединений, исключая время. Уравнение неподвижной оси получается из(2). Уравнения перемещенных аксисоидов получены из(3). Определите угол наклона половины раствора конуса, который образует неподвижную и подвижную акусоиду (рисунок Б). Введите _y = 0, чтобы найти значение
Аналогично определите угол наклона раствора оксида, подлежащего перемещению, предполагая, что y} = 0 ТТ «а = б — = 31.73. Движение твердого тела вокруг неподвижной точки, которое рассматривается в этом вопросе, называется нормальным precession. As в результате этого движения угол движения 6 остается постоянным, а угол прецессии φ и чистое вращение cp изменяются пропорционально времени. Если векторы coj и o> 3 (Рисунок B) образуют острый угол, то прецессия называется Prima.
Если этот угол тупой, то прецессия называется обратной кинематикой. Для прямой прецессии собственное вращение твердых тел и направление вращения мгновенных осей совпадают. При обратной прецессии эти вращения противоположны. Задача 7.2.При условии выполнения предыдущей задачи определите не только ускорение точки M, но и мгновенное угловое ускорение твердого тела(XYY 2). Решение.
Мгновенное угловое ускорение твердого тела равно скорости конца вектора мгновенной угловой скорости со. Из решения предыдущей задачи (рисунок B) видно, что вектор co описывает конус вокруг оси z с угловой скоростью o). рассмотрим О как радиус-вектор эструса твердого тела, вращающегося с угловой скоростью о)! вокруг оси z найдите скорость движения точки e zgo. 8 = <щ, х » — (о Кроме того, согласно предыдущей задачной зависимости(1) 0 — < я) и J (03.(2) Если ввести это значение o>в (1), то оно выглядит так: Р = ПХ х («1-р > с)= ф> Я х»-(3)
Из этой формулы следует, что вектор мгновенного углового ускорения направлен перпендикулярно плоскости zzx (рисунок а в предыдущей задаче), то есть вдоль линии узла. Если прецессия является прямой линией, то угловое ускорение соответствует положительному направлению линии node. In при обратной прецессии вектор r направлен в отрицательном направлении от оси ON. Величина мгновенного ускорения определяется из (3) £ = » )! 。 w3 sin 6 = 2-30 sin-g — = 30 секунд
Мгновенное угловое ускорение может быть найдено другим способом методом проекции. Согласно формулам (13) и (14) проекция углового ускорения на неподвижную и движущуюся координатные оси соответственно определяется как производная по времени от соответствующей проекции мгновенной угловой скорости. Поэтому найдите проекцию углового ускорения на неподвижные координатные оси. ех = у> ^ = р (15 грех 2Т) ’ = 30, потому что 2 /、 ey = J) v =(-15 cos 20 ′ = 30 sin 21% Т2 = к), = Гзо Кос | — Р 2) ’= 0.
Проекция углового ускорения на движущиеся оси выглядит следующим образом: £д -,= ж, =(грех 30/) ’ = 30, потому что 30 /、 syi = =(cos 300 ′ =-30 sin 30 /、£» = ^、=(2cos | + 30j = 0. Величина углового ускорения е = Вт%+ 4 + х | = + е * + е, = 30 Направление углового ускорения определяется Косинусом. потому что(Е, Х)= — £ — = с COS 2/, потому что(е = — £ -= грех 2/, потому что(Е, Р)= 0, потому что(е ^ я)= Косинус 30 /、 потому что(е, г) = — Син 30 /、 COS(8 ^ 0 = ^ = 0、
Угловое ускорение будет ориентировано вдоль линии узла. Переходим к определению ускорения в точке M. используя формулу (22), находим проекцию ускорения эструса M на движущиеся координатные оси. шхд =-30 грех 30 /•5 -С. С. 4-грех 30 /(sin 30 /.2-F cos 30 /.3 4-31,73.5)-1008-2、wvl = −30, потому что 30 /. 5-й.- — Джей-потому что 30 /(грех 30 /.2-j-cos 30 /•3 + 31.73 да.5)-1008-3, ВР = 30 потому что 30 / −3-Дж-30 Син 30 / −2 — Дж.- 31.73 (Син 30 /•2 -J-cos 30 /•3 -р 31.73•5) −1008.5.
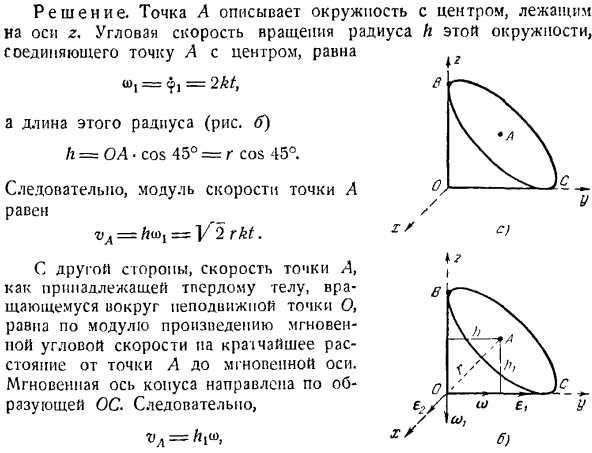
Ускорение точки Af, но найденная проекция определяется уравнением Вт = WX с ІХ + Wyj \ — ф ш£lklt Где илт Дзи, Фе являются опорой оси ХL. г[} зы Задача 7.3. Конус с углом в верхней части BOC= [y неподвижный шар С nirno в точке o, катятся без скольжения по плоскости XY. Точка а в центре основания конуса представляет собой окружность, центрированную по оси Z. Перпендикуляр, который опущен от A до Z, вращается вокруг оси Z в соответствии с уравнением. г = КЛ \ Радиус г основания конуса. Определить угловое и угловое ускорение конуса, а также скорость и ускорение течи A, B, C. Скорость и распределение твердых тел, вращающихся вокруг неподвижной точки, определяются по формуле <о =(о х г、 Где
Решение. Точка A представляет собой окружность с центром на оси Z. Угловая скорость вращения радиуса h этой окружности, соединяющей центр с точкой A, равна з= ф= 2 кт、 И длина этого радиуса(рисунок b) Ч = ОА•в COS 45°= г соз 45°. Итак, коэффициент скорости точки А равен Ва = ла> 1 в 2 РКТ. С другой стороны, скорость точки А, принадлежащей твердому телу, вращающемуся вокруг неподвижной точки о, равна произведению модуля упругости, мгновенной угловой скорости и кратчайшего расстояния от точки А до мгновенной оси.
Мгновенная ось конуса направлена вдоль ОС bus. So … ва = привет» > $ С.) Я… / Где hx = h = r cos 45°.Если мы сравним 2 значения, полученные для скорости точки А, то получим: У)= У)Л = 2kt. От 7.3 до задач. Используется в выражении / Скорость течки является параллельной оси абсцисс. Для наглядности сопоставьте положительное направление оси. Тогда о>!Но он направлен в отрицательном направлении вдоль оси z и направлен в положительном направлении вдоль вектора (ось o-y) (рисунок b).
Приступим к определению углового ускорения. £-8, — Ф Е4、 Куда? д <О э.=- о) ЕІ = 0)я dt. Тогда, в нашей задаче е=•(о0、 Кроме того, единичный вектор мгновенной оси показывает, что вектор я направлен в положительном направлении оси Y(рис. 6). Абсолютное значение 2-й составляющей углового ускорения равно е.) = в Sin 90°= 4 * в И он направлен в положительном направлении вдоль оси x(рисунок b). Поскольку эта точка находится на мгновенной оси, скорость эструса C равна нулю.
Скорость точки B равна абсолютному значению vQ-2va = rkt, минимальное расстояние от точки B до мгновенной оси О = 2Л. Вектор vB ориентирован параллельно оси x в положительном направлении. Переходим к определению ускорения. Ускорение точки С равно ускорению уравнения Wc = W°rc + W£P 4 ″ WcPs Точка С находится на мгновенном axis. So … ж ° СС = 0. Точно так же (8,|] rs и т. д.). Так… туалет = Т » ДЖИПИ = = е 2Xgs. Ускорение точки С равно абсолютному значению туалет = в Sin 90°, Е2 г = 4 РК * Т * 1 ^ 2
Затем его направляют параллельно оси z (рисунок c).Ускорение точки B равно ускорению уравнения ^ = Иго = 0 в Сильное ускорение точки B равно по величине W°BC = OB * u> 2 = 4] / T rkH * Он направлен от эструса B к O (рисунок c). Ускорение X£jJ} p направлено параллельно оси x(рисунок C)、 По модулю * o> я»Р =£. OM * sin 90°= 2) LG rk. Ускорение wBB ^направлено параллельно отрицательному направлению оси y(рисунок C), равному модулю = * OBsin 90° = 4)^ 2 ″ коэффициент ускорения в точке rk4 \B wB = V w < * {- f WX + WZ — = 2rkV 16A ^ 4 + 2.
Ускорение точки А определяется следующим уравнением =™°АС + В7,+ ВЗ Постоянное ускорение — это модуль жек =(Дж) 2fii = 2} / <ГhkCh * Он направлен вдоль кратчайшего расстояния от точки А до мгновенной оси, то есть вдоль а(рисунок б).Первая составляющая ускорения вращения ®ДЖП= | e1Xril | = е, rsin 450 = VR2 и » РК Причем он направлен параллельно оси x (в положительном направлении).Абсолютное значение 2-ой составляющей ускорения вращения равна ш » л = J В Е * Х га | = ЕАГ = 4 rk4% От А до Б
Ускорение точки, движущейся по окружности с радиусом h (рисунок B), равно уравнению wA = wnA + w\, где нормальное ускорение равно ЗП. =Λ= A r L 1 Причем он направлен вдоль кратчайшего расстояния от А до оси Z. Тангенциальное ускорение равно ш \ = УТ РК в ДТ И он направлен параллельно оси X. При сравнении обоих решений、 вап = ш \ шя,= ш°п Косинус 45° D (L) A LL И проекция эстрального ускорение, Z-ось а-ось равна пулю В2 = в COS 45°-= 0 Ускорение в точке А находится на плоскости, параллельной xy.
To овладев навыками решения задачи о вращении твердого тела вокруг неподвижной точки, И. В. Мещерский из сборника задач по теоретической механике в 1950-х и более поздних изданиях рекомендует решать следующие задачи:696、698、599、604、607、 610 В отличие от уравнения(4), координаты x, y и z меняются со временем, но в уравнении(5) величины xi и ylt zx являются координатами точек тела движущейся оси, связанной с твердым телом. Естественно, эти координаты не меняются.
Проекция угловой скорости на неподвижную и движущуюся оси координат, содержащихся в формулах(4 *) и (5.}:), вычисляется из известных углов Эйлера по следующей формуле: (6 *) * Ф ω== > > k + Qn 4 — COS 0 ty (Да Так…
Где (lu} w2-проекция угловой скорости на неподвижную ось координатного пакета. 「• о) грех 9, Си грех +Ocos 9、•• а) yj = 6 sin 6 cos 9-0 sin 9 у)Зи =φCOS 6 Где oi^, u> Zl-проекция угловой скорости на движущуюся ось. Мгновенная угловая скорость в (1ч) = * + + О4 + потому что) Момент оси геометрического МЕЗГО, отмеченный в фиксированном пространстве, называется фиксированным Аксоном. Уравнения с фиксированной осью Движущаяся ось x-это геометрическое положение мгновенной оси, вырезанной в движущемся теле.
Уравнения движения в Матрице _ Г \ _ _ з> _ Осадок. Аль. Угловое ускорение твердого тела является производной вектора угловой скорости относительно времени — Г-(12 *> если рассматривать = ТТ -Первая составляющая углового ускорения, которая направлена вдоль мгновенной оси и характеризует изменение угловой скорости Размер.2-я составляющая углового ускорения Характеризует изменение угловой скорости в направлении. 0)!Скорость вращения вектора о>является: в. −1? = («>Х (г 0. И затем… Помимо использования приведенной выше формулы, для нахождения углового ускорения используется и другой метод определения е.
Это делается через проекции углового ускорения на фиксированной оси или через стационарный подключен сис движущегося твердого тела. Проекция углового ускорения на неподвижную координатную ось задается формулой: ДТ ’ £>’ — Ди> ДТ ’ с) Проекция углового ускорения на движущуюся ось, плотно соединенную с корпусом, равна д ^ ХХ <4,^ Ускорение точки твердого геля, вращающейся вокруг неподвижного центра, равно сумме оборотов I ускорения после эмиграции (теорема соперника) .ОС | ВР ВМ = в> М + ВМ Ф Куда? Угловое ускорение е = е+ е.2>
Ускорение вращения определяется следующим уравнением „ED =“ ff,+ — » I X G + e2 x g. значение устойчивого ускорения — ФЛ (Чи\ //- Кратчайшее расстояние от точки до мгновенной оси. Это ускорение направлено вдоль перпендикуляра, который висит от точки к мгновенной оси (рис.7.3).Значение ускорения вращения ^> 5}=//, e, (19 *) Где HT-кратчайшее расстояние до оси углового ускорения вектора(рис. 7.3).Направление ускорения вращения определяется правилом векторного произведения. Осестремии и ускорения вращения, вообще говоря, не перпендикулярны друг другу.
Это Формула (16), (17% Однако эти жесткие точки существуют и сейчас. Рений теперь перпендикулярны друг другу. Геометрическим расположением этих точек является плоскость в твердом теле, проходящая через векторы co и R. Поскольку известны устойчивые и вращательные ускорения, коэффициент ускорения точки можно определить по следующему уравнению: ВМ = В (Ш%) — Л- + 2Вт%. ж%соѕ(п-т ^ п). (20 *)
Проекция точечного ускорения на неподвижную ось равна серии WX = tyz-ГГУ + о)Х (сорь:-е * ый + < & ЗЗ) -’ =- exz + тай(тссс ууу-у sh2g)-(9] *) = £ху-в * + <* *(10х * + <в ± Проекция точечного ускорения на движущуюся ось определяется по формуле: * ’ХВ =—Ф wjci-Ф З» ^ я)- Wyi = = tzxxx — ^ K. Jfi — (22 *) = — £.Ви * и-Р-младшего «гггг» — а). Данный комплекс действий рекомендуется для решения задачи определения скорости и ускорения твердых точек, вращающихся вокруг неподвижного центра. A. уравнения движения даны в виде углов Эйлера как известная функция времени. Угловая скорость и угловое ускорение твердого тела, уравнение движущегося тела, и
Смотрите также:
Предмет теоретическая механика

