Оглавление:




Определение сил в затянутых резьбовых соединениях
- Определение силы в креплении Резьбовое соединение Винтовые соединения, как правило, затягиваются. Сила затяжки, которая тянет винт и затягивает соединяемые детали, создает большое давление на стыки и винты, что исключает возможность взаимного смещения деталей. Внешняя нагрузка соединения может быть осевой (направленной вдоль оси винта, пытающегося открыть
соединительную часть), поперечной или комбинированной. Осевая внешняя (рабочая) нагрузка F (рис. 15.6). Необходимо для надежной работы соединения растянуть винт (расчетную нагрузку), определить полную силу и затянуть усилие G8at с помощью Fpac. Для риса. 15.6, и указывает на свободное соединение.
При затягивании соединения под действием силы тяга винта растягивается на определенную величину, а соединяемые детали(фланцы) укорачиваются на Людмила Фирмаль
величину DD. 15.6, б). При этом, начиная с равновесного состояния, сила растяжения винта равна силе сжатия фланца соединяемых деталей. Вы можете графически выразить связь между силой и деформацией, основываясь на законе крюка(рис. 15.6) 349 по прямой линии с шагом угла наклона равным обратному коэффициенту податливости винтовых деталей HV и HD : Один. Г. Т. М «а»» Один. Положение прямой справа и слева от оси нагрузки F связано со
знаком деформации: укорочением фланца детали и расширением винта. Он показывает деформацию винта и детали на рисунке. 15.7, основываясь на законе крюка AB=^ZAT^a, Ad=F ZAT^d * после приложения внешней нагрузки F (например, давление газа создается в цилиндре с завинченной крышкой), шток винта равен 15.6, по величине DV). Отложите в сторону на рисунке(см. диаграмму. 15.7) с деформацией DD да, графически получим величину суммарной силы, растягивающей винт F’4 и остаточной силы затяжки Ki F’3ar,
- сжимающей фланец. На графике видно, что усилие растягивания винта увеличивается на величину Fa=d; tg FW=d; DV. Усилие сжатия детали уменьшалось на величину^d=DD tg FD-DD. (Если мы подставим выражение (15.1) после’GA4-DG=F ‘ из состояния равновесия и решим его относительно F B, то получим P b=N d/(Xd4-X,). Коэффициент соответствия равен%: X=HD/(HD4-XV) (15,2) И назовем коэффициент внешних нагрузок. Затем, если добавить усилие затяжки винта от внешней нагрузки F, то оно будет из Формулы (15.2) равно F B=.) 350видно, что % 0. Из графика (см. диаграмму. 15.7) Fsar=FpaC4-F=F3 «+xF-F=F3 » — F(1-x)>0;следовательно, F3aT>F(1-x). Принять Fmt=vF(1-x), Где v-коэффициент крепления, v=1,5…2 при статической нагрузке,
v=2,5…4 под переменной нагрузкой. Из графика следует, что расчетная нагрузка=+ = (1-X)+XG;f»,=f[>'(l-x b x L (15.3) напряжение зажима выбрано как o3at=(0.5)… …0,6) от. Величина усилия затяжки критического соединения связывает осевое усилие завинчивающегося Болта (штифта), создаваемое удлинением Болта (шпильки) или специальным калиброванным ключом, с моментом завинчивания (6.8), как показано в главе 6. Определение коэффициента внешней нагрузки X -как видно из Формулы (15.2), значение коэффициента податливости винта XA и детали XD должно быть известно для того, чтобы определить коэффициент X. Винт постоянного сечения для HV= / V / £VLV, (15.4)
Где<4a=ndp/4; dp-расчетный диаметр резьбы; dp=d-0,94 P; d и P-наружный диаметр и Людмила Фирмаль
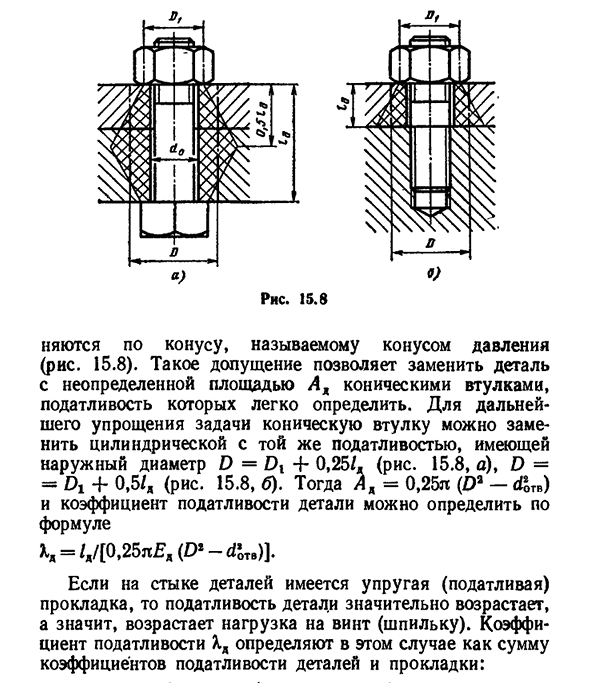
шаг резьбы соответственно. Коэффициент податливости соединенных деталей HD определяется исходя из предположения, что деформация детали распространяется- 351 страница. 15.8 Они разделены конусом, называемым конусом давления(рис. 15.8). Это предположение позволяет заменить деталь неопределенной областью. Для дальнейшего упрощения задачи коническую втулку можно заменить цилиндрической втулкой, обладающей такой же гибкостью, с
наружным диаметром D=Dt4-0,25/. (Рис. 15.8, А), D= = Di4-0.5/d (рис. 15.8, б). Тогда LD=0,25 l(D2-d’TB) и коэффициент соответствия детали можно определить по формуле KK=/d/[0,25 l (D2-d’TB)]. Наличие эластичных (гибких) прокладок в местах соединения деталей значительно повышает гибкость детали и увеличивает нагрузку на винт (штифт). В этом случае коэффициент гибкости HD определяется как сумма коэффициентов гибкости детали и распорки: х ^D1^D1 (15.5)
Смотрите также:
Решение задач по деталям машин
| Паяные и клеевые соединения | Расчет болтов на прочность |
| Типы крепежных деталей | Расчет соединений, включающих группу болтов |

