Определение сил по заданному движению

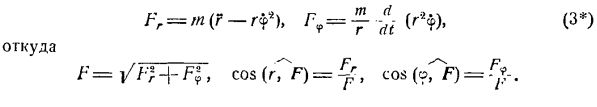
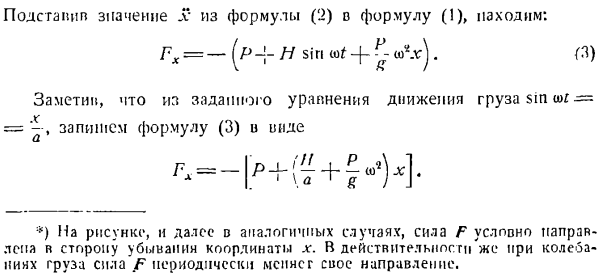
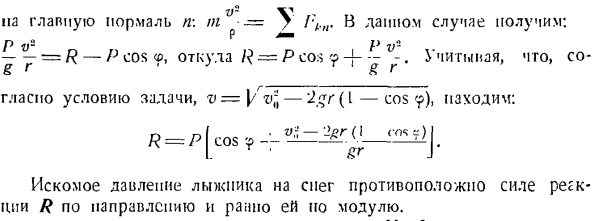
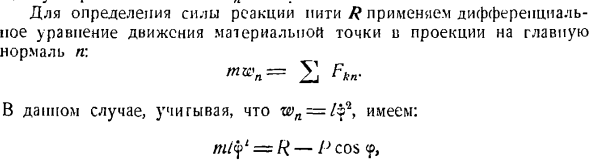
Определение сил по заданному движению

• Определение силы по конкретным движениям (Прямая задача динамики важных точек） Если уравнение импульса для точки массы mn задано в декартовых координатах: x -} \ ( / ), y = / a（/）、= = /、（/）、тогда проекции ΓX, yy и F, силы F-Fxi-j-FJ ^ — Fk для вызова этого движения определяются по формуле. Форекс = MXF и ФЗ = МЗ,(я ） Откуда? Ф = Я / интернет + ТФ-Н-Т、 потому что(ХГ>)=, потому что(г? Ф)= YG может, потому что(Z7 резца-Ф)=.

Поэтому прямая задача динамики важных точек может быть легко решена путем дифференцирования некоторого кинематического уравнения точек. Дано уравнение движения массы точки m вдоль траектории, то есть a = f (), проекции силы F = F Fn и Fh. R «r t-nn+, который вызывает это движение, определяется по формуле: Форекс = Ма£, рН = mvyt ФБ = 0, (2 ） Откуда? F = / F; — rn> cos (Γ>)= y, cos (Г>)=^, cos(0)= 0 В Формуле (2) vx =〜.

Сопротивление движению является функцией скорости лодки. Людмила Фирмаль

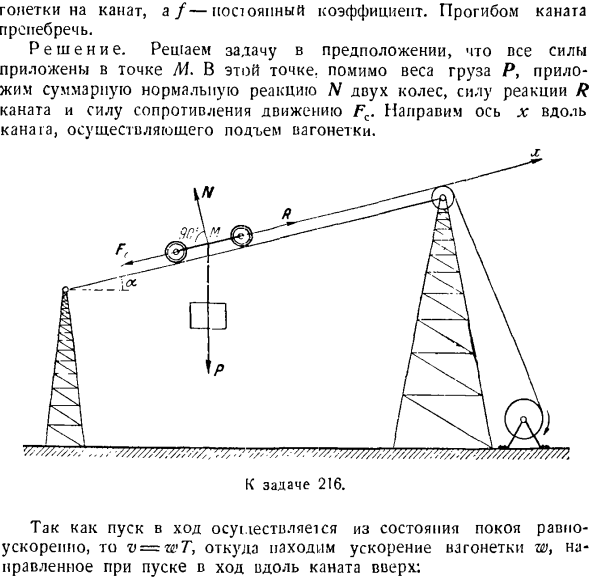
Учитывая уравнение планарного движения точки массы m в полярных координатах r = / 1 ( / ), синоу + ФК +£*. (Да б. Так… = / 7В = ФП потому что А, х = Ш = ^ Г、 Α= Р(синоу + / соз + ^ И я При равномерном движении тележки L * = 0, а Формула(1)принимает вид: Р = р(грех от J — / соз а). Требуемое натяжение каната равно модулю отталкивания R. задача 217.Масса Р определяет сопротивление воды движению лодки. П. С. x = — vQ(1-e p), где x> 0-средняя скорость движения, и- О Фиксированный коэффициент. Н. С. С. Цель 217.

Решение. Сила, приложенная к лодке: P-вес лодки, N-нормальная сила реакции воды, R-сила сопротивления воды движению лодки, а также направлена на противоположную сторону движения. проекция скорости лодки на ось Х — aJLt ЧХ = х * = vQe стр. (Т） Проекция ускорения лодки на ось x = = (2） напишите дифференциальное уравнение для движения лодки, спроецированной на ось X. Р М Л г. Используя формулу(2), можно увидеть следующее: [В] ГХ = — avttc». По условиям, сопротивление jR является функцией скорости лодки, поэтому при приведении Формулы (1) получаем Rx =-avx.

• Проблема 218.In в соответствии с Формулой x = a sin +Н грех о) Т—7 а -). (1） Потому что, согласно данному уравнению движения, как x = \nut, n = — aui1 sin mt, т. е. х = — » л . (2） Подставляя значение l из Формулы (2) в Формулу (1), получаем: Γχ= — [pI sinЫ+ » Лг)). (3） Из уравнения движения заданной нагрузки sin= запишем Формулу (3) в виде: * ) На рисунке, в дальнейшем аналогичном случае, сила F направлена условно на R-уменьшенную сторону x-coordinate. In дело в том, что даже во время колебаний нагрузки сила F периодически меняется:

x = a, t. in в случае s при самом низком положении нагрузки сила упругости F достигает максимума 31 апексии. То есть, когда нагрузка проходит через положение статического равновесия. когда V = 0, сила упругости пружины равна весу груза. Задача 219.Автомобиль ve и P = 1200 кг движется по дну каньона с постоянным модулем скорости и= 36 км ’ НС. Определите давление автомобиля на дно оврага в наиболее интересующей точке. Радиус кривизны траектории p в этой точке равен 50 м, и мы будем рассматривать транспортное средство как точечную массу. Игнорируйте сопротивление движению.

Примените дифференциальное уравнение движения для массовой точки проекции к главной нормали Людмила Фирмаль

Решение: используйте естественную трехгранную ось, направив ось m горизонтально вправо, а ось n вертикально вверх. 2 силы приложены к автомобилю и приобретены как масса пункта. Масса P и нормальная реактивная сила R грунта, направленная вертикально вверх вдоль основной законной линии. //： С. С. В этом деле С. С. Откуда? 。 П. В.- С9. Если подставить число, то R = 1445 кг.

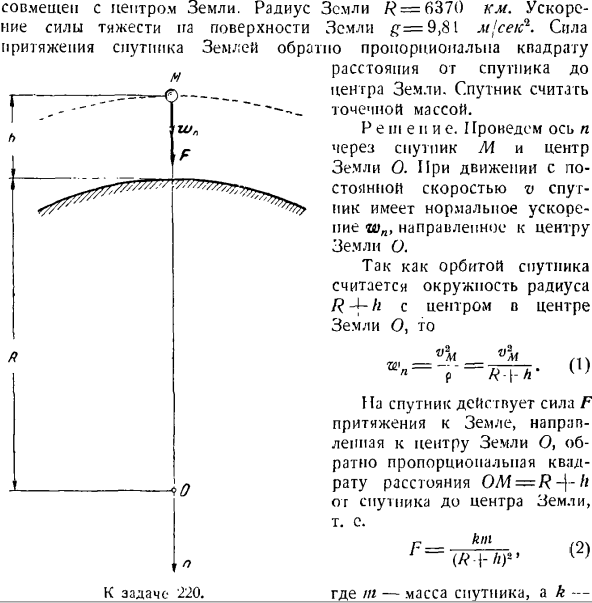
Требуемое давление транспортного средства на дне каньона направлено в противоположную сторону к нормальной силе реакции R, и величина ее равна. Проблема 220.Определите скорость, с которой спутник движется на высоте/ 2 = 900 км, если орбиту спутника можно сделать почти круговой в центре В сочетании с центром Земли. Радиус Земли а? = 6370 км. Гравитация земной поверхности гравитация£= 9.81 м \ сек \ спутника обратно пропорциональна квадрату Расстояние от спутника до центра Земли. Спутник считается точечной массой.

Решение. I ось Гройсмана n проходит через центр Земли O со спутником M. При движении с постоянной скоростью v спутник имеет нормальное ускорение wn, которое идет к центру Земли O. Так как орбита спутника представляет собой окружность радиуса R 4-h, центрированную по центру Земли O、 м. / — — — — — О —- То… ш= -^ — = «Го» Третий 0.） Я ’ Спутник находится под влиянием притяжения Земли к Земле, которое направлено в сторону центра Земли O, и обратно пропорционально расстоянию от спутника до центра Земли OM = R-]-H2. п = ._ км(2）

Да. н. К выпуску 220. ’(А * |-а) 2 «в» Где t-масса спутника, к- Ф — М(7-Ф£(Р!Φ), (3 *） Откуда? / ’ = / / .•; + ФДЖ, потому что(Р>)=^, потому что(φГ>)=^ -. Коэффициент пропорциональности. Что находится на поверхности Земли, то есть если h = 0, l:= P = mg, мы узнаем из уравнения (2): k = gR. Следовательно, гравитационное притяжение Далее пишем дифференциальное уравнение движения спутника и, как точку материи, проецируем его на ось N. мзн = Ф Используя Формулы(1)и(3), получаем следующее: , н \ я nifrR * И затем） IFL 4-NU vM = R j / » = 7,4 км лед k.

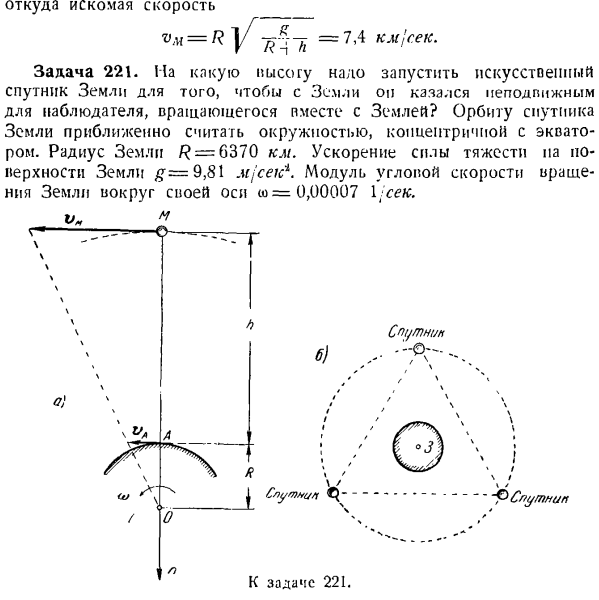
Где находится желаемая скорость Задача 221.At на какой высоте необходимо запустить искусственный спутник Земли, чтобы вращающийся наблюдатель с земли не казался сдвинутым с места искусственным спутником? Приблизительно предполагается, что орбита спутника Земли представляет собой окружность с экватором и концентрическую. Радиус Земли/? = 6370 км. Гравитационное ускорение земной поверхности # = 9.81 Мдж’Сик модуль угловой скорости вокруг земной оси равен= 0.00007 1 сек. Да.

Перейдите к выпуску 221. Спутник ^ Слу / ННК / ТКВ » б.） один.] 「* \ / / / У СГ / utnip да……. Гравитация спутника Земли обратно пропорциональна квадрату расстояния от спутника до центра Земли. Спутник считается точечной массой. The solution. To сделайте его похожим на искусственный спутник, который движется по экватору и концентрическим орбитам от Земли, пройдите через ось n, проходящую через спутник A, центр Земли O, и наблюдатель A на экваторе, и посмотрите на Землю (см. Рисунок A, схема Земли от Северного полюса).Согласно этому условию, скорости спутника M и наблюдателя 

A должны удовлетворять следующему соотношению. _ Ом. ВА ОА ’ поскольку r> d = A> w, t0-отклонение угловой скорости вращения Земли за 1 день вокруг Земли: eV, R = R -/, OA = R, w v. w =(R•!- / / ) быть. Для предыдущего выражения задачи (-1) Это значение V. подставляя вместо ii, мы видим, что: (R-Λ)=^. г / м — / о -’ Где находится нужная высота * == Подставляя цифру, вы найдете нужную! Высота 36800 jc. tf. Существует проект по запуску 3 искусственных спутников на эту высоту, чтобы сформировать равносторонний треугольник, на вершине которого находятся спутники. Подумайте о том, чтобы не двигаться

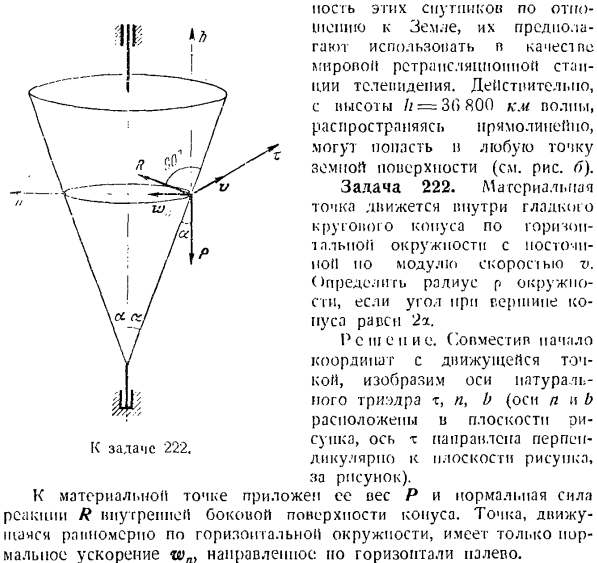
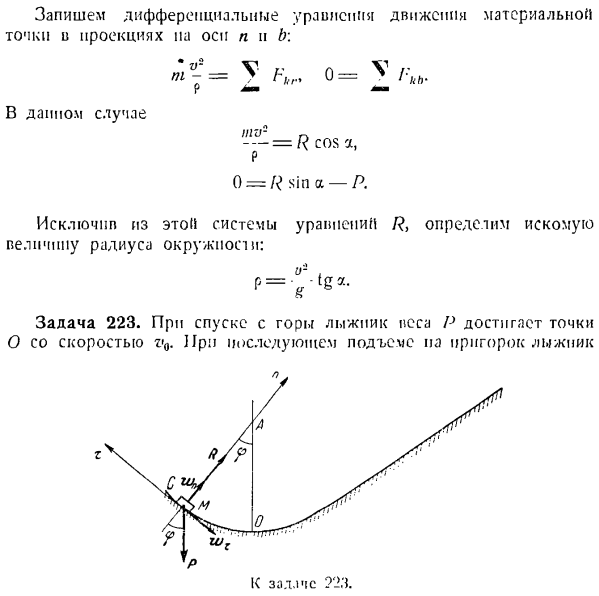
HOC l b этих спутников предполагается использовать в качестве всемирной телевизионной ретрансляционной станции по отношению к Earth. In дело в том, что с высоты// = 3 (>800 км) волны, распространяющиеся по прямой, могут достигать любой точки земной поверхности(см. Рисунок Б). Задача 222.Точка массы является пост-темпом, но движется в гладком конусе вдоль горизонтальной окружности по модулю скорости V. Если угол вершины конуса равен 2a, определите радиус окружности p. R и W E.

выравнивает начало координат до точки движения и изображает естественные трехгранные оси m, n и b (оси n и b «»’ находятся в плоскости 222 на supps ось x направлена на преступника. Особенно на плоскости изображения, для каждого изображения). Вес P и нормальная сила реакции R на внутренней поверхности конуса приложены к точке массы. Только нормальное ускорение wn}направлено к точке, которая равномерно движется по горизонтальной окружности.

Горизонталь-это олененок. Напишите дифференциальное уравнение движения точки масс в проекции осей n и b. = В 0 = УКБ. В этом деле ИГ — — — = Р потому что, п О = Р грех-Р Исключение R}из этой системы уравнений определяет искомое значение радиуса окружности. Р = vtga- Задача 223.При спуске с горы лыжник с весом P достигает точки O на скорости v0.Затем, когда вы поднимаетесь на холм, лыжник Проблема 72’x. Вдоль дуги окружности OS радиуса r скорость v = Y vij — ’2gt•((где’ f-cos-угол, образованный вертикальной линией и радиусом AM. Считается как точечная масса. Решение.

Траектория катания известна. Изобразим естественное трехгранное естественное по, определив его происхождение в точке А/, занятой текущим лыжником. К лыжнику были приложены следующие усилия. P-лыжная собака, обычная сила реакции снега, которая идет от M к центру L по радиусу дуги R-OS. Представляет нормальную wn и касательную w. компоненты ускорения лыжника. Примените дифференциальное уравнение движения к проекции для определения нормальной силы реакции R В. В.•

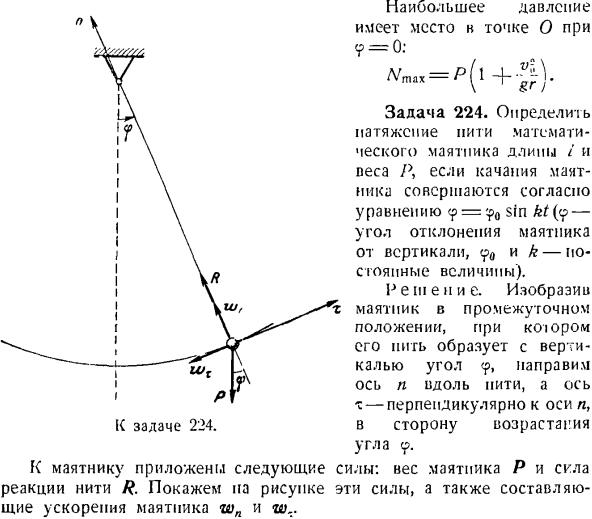
Основной нормальный n \ t■ -=?В этом случае P v-P v- — г = р-в ^ ОС <р, Где р = р что? — Дж.^—В зависимости от рассматриваемого условия v = [/ rv *-2 gr(I-cos 9）、 г гл•<Г)С Д)| R = P I cos 9—— нет. Требуемое давление лыжника на снег представляет собой модуль с реактивной силой R в обратном направлении. Максимальное давление возникает в точке O, 9 = 0. Задача 224.Когда маятник качается уравнение<? =?0 грех КТ {<?Угол отклонения маятника от вертикали.<p0 и k-постоянные значения.) Решение.

Мы изображаем маятник в среднем положении, и его igi образует вертикальную линию и угол 9, поэтому мы направляем ось n вдоль нити, а ось x перпендикулярна оси n, в направлении, в котором угол 9 увеличивается. К маятнику приложена следующая сила: масса маятника Р и сила реакции нити р. На рисунке показаны компоненты ускорения этих сил и маятников wn и W. Цель 224. Для определения силы реакции нити R используют дифференциальное уравнение движения точки массы в проекции на главную законную линию n \ В этом случае wn = l $ <it, это выглядит так: млй = р-р с COS <Р、

Если во время движения его линия действия проходит через неподвижную точку, которая называется центром, то сила, приложенная к материальной точке, называется центром. Сила, направленная к неподвижному центру, называется гравитацией. Сила в направлении от неподвижного центра называется разрушающей силе. Движение материальных точек под действием Центральных сил происходит в плоскости через радиус вектора и начальную скорость движения points.

To изучите его, удобно ввести полярные координаты и использовать формулу Bipe. df \ r J’G 4mC «» Где C-веерообразная скорость точки, которая постоянна при наличии центральной силы. C=—S = y (скорость сечения Называется производной по времени от площади, описываемой вектором радиуса r движущейся точки.） Применение формулы Bipe позволяет определить закон изменения нейтральной силы из некоторого уравнения центральной орбиты (прямая задача). Если Vr положительна, то центральной силой является сила отталкивания, а если она отрицательна, то это сила притяжения.

Рекомендуется решить прямую задачу динамики несвободной материальной точки, где необходимо определить заранее заданную силу и силы реакции, приложенные к точкам l и s и l в следующем порядке. 1) изображающ важные пункты настоящего положения, и силу установки приложенную к напитку. 2) примените принцип высвобождения связи, чтобы изобразить силу реакции соответствующей связи.

Откуда? Так что насчет условия c? = г Необходимое натяжение нити Т направлено в противоположную сторону к силе реакции#, равной модулю силы реакции#. Проблема 225.Точка массы движется под действием центральной силы логарифмической спирали. Форма уравнения: r = ae-x? Как добраться туда, где a и X являются константами. Определяет закон изменения центральной силы. Решение.

Использовать выражение Биазе когда мы получаем 2-ю производную на cf, мы видим, что: / п(). 11й * \ Г Я А Г Подставляя это значение в венское уравнение и решая уравнение Fr, получаем: Где A = 4 /и C2(1 знак минус-центральная сила、 Перемещение материальной точки по логарифмической спирали является силой притяжения. Эта сила обратно пропорциональна кубу на расстоянии от неподвижного центра.

Напишите уравнение логарифмической спирали в виде: 3) Выберите справочную систему, если она не указана в состоянии проблемы. 4) определить ускорение точки масс по законам заданного движения и найти ее проекцию на выбранную координатную ось. 5) создать дифференциальное уравнение движения точки масс, соответствующее принятой системе отсчета. 6) из системы комбинированных уравнений определить искомое значение. При решении прямой задачи динамики материальной точки необходимо определить результат действия силы, приложенной к этой точке, решение задачи заключается в выделении данного кинетического уравнения точки с помощью

Формулы(1), (2) или плоского движения (3*) уравнения. Задача 211.Точка масс движется по формуле x = at, y = bt. Где A и B-константы. Определите силы, которые вызывают это движение. Решение. Проекция искомой силы на ось декартовых координат определяется по формулам Fx — = mx и Fv = my. Найти Йк = г = 0, используя данное уравнение движения. Итак, Форекс = ФГ = 0, т. е. ф = 0. Эту задачу можно решить и другим способом-определив траекторию и скорость движения точки. Точки движутся по прямой y = — x с постоянной скоростью v = / a2 + b%.So, согласно принципу инерции, F = 0.

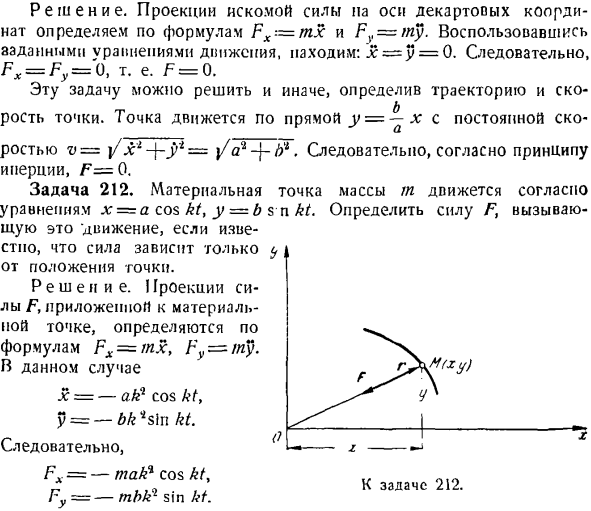
Проблема 212.Массовая точка m перемещается по формуле x = A cos kt, y = bsnkt. Если вы знаете, что сила зависит только от расположения точек, определите силу F, которая вызывает это движение. Решение. Проекция силы F, приложенной к точке массы, определяется по формуле Fx = mx, Fy =в этом случае х = — с обеих сторон, потому что КТ、 г = — ьк * СЛН КТ. Так… Форекс = — так * потому, КТ, ФГ = — mbk1 грех КТ. К выпуску 212. По гипотезе, сила F зависит от расположения точки масс, поэтому ее проекции Tx и Fy являются функцией координат x и y. используя уравнение движения точки, оно выглядит так:

Форекс = — mklxy ФВ = — миры. Коэффициент сила F, ф == ^ ф} + ФГ = чернильный * л / х * + У2 = mklr、 Где r-модуль векторного радиуса массовой точки r = OM. Направление силы F определяется с помощью направляющего Косинуса:^ ^ потому что(Л, Ф)== -, cosCv, Ф)=?у =-2. Y и^соответственно, чтобы определить угол, образованный осью В случае X и y радиуса вектора сила направлена от M к O. таким образом, эта материальная точка движется под действием силы притяжения к центру O, которая является модулем с F в качестве закона. Эта сила называется центральной. Задача 213.

Масса вещества m движется по окружности радиуса a по формуле c = bt. Определите силу, которая вызывает это движение(A-координаты дуги, b-постоянная величина). Решение. Использует естественные трехгранные оси N и b. Проекция искомой силы на ось=они определяются по формуле. г Сив. в.- Задача 211. = ФБ = 0. Алгебраическое значение скорости точки- (ЛЗ вы можете видеть, что = v — = b. поэтому： №. Серии WX =:0, ЗП =-=-. .Р б.- Таким образом, Px = 0, Fn = in -,= 0, т. е. сила T7、 Заданным движением материальной точки является рад Б.- Окружность борода находится в центре, а по модулю равна m -. Задача£14.Вес P =Я00кг пассажирский подъемник опускается с ускорением w = $ 0,4.Где g-ускорение свободного падения. Определить натяжение опорного троса, если перемещение резистора F равно 0,2 от веса лифта. Решение.

К лифту прикладывается заранее заданная сила-масса Р, сопротивление движению F, направление, противоположное движению, то есть направленное вертикально вверх. Примените принцип releasable™или сцепления, чтобы мысленно проанализировать кабель и компенсировать поведение секции отходов кабеля с реактивной силой R вертикально вверх. Пойдем по траектории движения лифта, то есть к оси Х в вертикальном направлении.

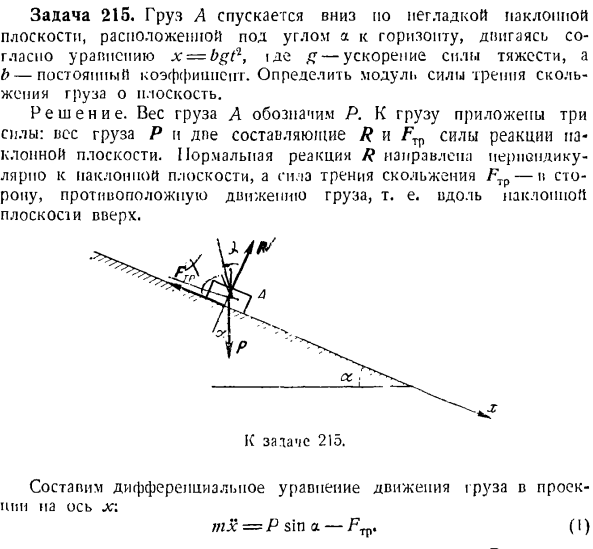
Запишите производную уравнения движения точки материи, спроецированной на ось lr. н. Техас= В этом случае существуют: — х-Р-Ф-Р、 О том, где Р.- =П-ф-Икс. К Учитывая= o; = 0.4^, a / 7 = 0.2 Р, выглядит так： Р = 0,4 Р = V20 Диск К>.Необходимое натяжение кабеля равно коэффициенту реактивной силы R. Проблема 215.Груз а спускается по гладкой наклонной плоскости, двигаясь по формуле х-БГП, под углом а относительно горизонтальной плоскости.> > де g-ускорение свободного падения, А B-постоянный коэффициент. Определите коэффициент силы трения скользящей нагрузки на плоскость.

Решение. Вес груза A выражается в R. 3 силы прилагаются к грузу. Вес груза P и сила реакции наклонной плоскости составляют 2 составляющие, R и FTr. Нормальная сила реакции R направлена перпендикулярно наклонной плоскости, сила трения скольжения FT?- По направлению, противоположному движению груза, то есть по склону создайте дифференциальное уравнение для движения груза, спроецированного на ось X. = Р ЗША — / в(я）

Смотрите также:

Предмет теоретическая механика

Динамика	Определение движения по заданным силам
Основные формы дифференциальных уравнений динамики материальной точки	Колебательное движение