Оглавление:





Определение сил инерции
- При движении звена механизма все движущиеся с ускорениями материальные точки действуют с силами инерции на смежные материальные точки. В результате совместного действия внешних сил и элементарных сил инерции в звеньях возникают напряжения. Силы, действующие на звенья, уравновешиваются силами реакции, возникающими в опорах звеньев, т. е. в кинематических парах.
Напряжения, возникающие в звеньях под действием сил, в теории механизмов и машин не исследуются, потому что, как об этом уже упомянуто выше, в теории механизмов и машин методы расчета звеньев на прочность не излагаются. Поэтому в дальнейшем силы инерции мы будем принимать во внимание только при определении давлений в кинематических парах.
При этом практически необходимо бесконечное число действующих в звеньях Людмила Фирмаль
элементарных сил инерции заменять равнодействующими силами и парами. Ниже разъясняется, какими равнодействующими силами и парами могут быть заменены все действующие в звеньях элементарные силы инерции. Производя замену элементарных сил равнодействующими, необходимо всегда иметь в виду, что никаких действительных равнодействующих сил в природе и технике не бывает: равнодействующая сила — это такая фиктивная сила,
которая, если бы она существовала и одна действовала, производила бы такие же давления на опоры звена, какие производятся всеми реально действующими элементарными силами. При определении равнодействующей силы мы должны выявлять ее величину, линию действия и направление. Точка приложения равнодействующей на ее линии действия при определении давлений в опорах звена не имеет никакого значения, так как по линии действия равнодействующая может быть перенесена в любую точку. Такой перенос точки
- приложения не может оказать влияния ни на величины и направления моментов, создаваемых равнодействующей относительно разных точек звена, ни на величины и направления сил реакций в кинематических парах. В некоторых случаях оказывается удобным линию действия равнодействующей переносить параллельно самой себе на некоторое расстояние. Такой перенос не будет оказывать влияния на величины и направления сил реакций в кинематических парах только в том случае, если при этом будут соответствующим образом изменены величина и направление
момента равнодействующей пары. Пере-Определение сил инерции 9? плокотосилы симтело 116. нося таким образом линию действия равнодействующей элементарных сил инерции, можно совместное действие на звено силы и пары привести к действию только одной силы. Ниже при определении величин, направлений и линий действия равнодействующих сил инерции при разных видах плоского движения мы будем исходить из предположения, что движущееся тело имеет хотя бы одну плоскость
симметрии, т. е. такую скость, по обе стороны рой все элементарные инерции Людмила Фирмаль
расположены метрично. Изображая на чертеже, мы будем изображать плоскость симметрии и будем предполагать, что все точки тела движутся в плоскостях, параллельных этой плоскости. Отмечая на чертеже точку приложения элементарной силы инерции, мы будем предполагать, что в эту точку перенесены параллельно самим себе все элементарные силы инерции, действующие в точках, расположенных на линии, перпендикулярной к плоскости симметрии в этой точке. Например, тело, изображенное в двух проекциях на фиг. 116, .будет иметь одну плоскость симметрии при
движении параллельно плоскости чертежа на фиг. 116, а или перпендикулярно к плоскости чертежа на фиг. 116, б. В таком случае под элементарной силой инерции, приложенной в точке х (фиг. 116, а), следует разуметь сумму всех элементарных сил инерции, действующих во всех материальных точках на линии х — х (фиг. 116, б) и перенесенных параллельно самим себе на плоскость симметрии. На фиг. 116, а изображено сечение тела плоскостью симметрии, а на фиг. 116, б линия а — а является линией пересечения плоскости чертежа с плоскостью симметрии. При движении этого тела в направлении, перпендикулярном к плоскости чертежа, на фиг. 116, а у движущегося тела не будет плоскости симметрии. Определение сил инерции, возникающих пря движении тел, имеющих более одной
плоскости симметрии, выходит за рамки настоящего курса. Звено плоского механизма может двигаться поступательно, вращаться вокруг неподвижной оси или совершать сложное движение. Во всех этих случаях сила инерции, как известно из теоретической механики, равна произведению массы звена на ускорение его центра тяжести и направлена в сторону, обратную ускорению центра тяжести. При поступательном движении линия действия силы инерции проходит через центр тяжести, при вращательном движении с нерав7 Зиновьев 61298 Кинетостатический расчет плоских механизмов номерной угловой скоростью — через центр качания, лежащий на
продолжении линии, соединяющей центр тяжести с центром вращения, и отстоящий от центра вращения на расстоянии равном J s Р2 * 5 1 mrs S rs где rs — радиус вращения центра тяжести; Js — момент инерции звена относительно центра тяжести; m — масса звена; р — радиус инерции, равный При вращательном движении с равномерной угловой скоростью полное ускорение центра тяжести равно нормальному, поэтому линия действия силы инерции совпадает с радиусом вращения центра тяжести. Сложное движение звена можно рассматривать как движение с ускорением какой-либо
выбранной точки звена и вращение вокруг этой точки. В этом случае полная сила Ри инерции получается как геометрическая сумма двух сил — силы Р’и инерции в движении с ускорением выбранной точки и силы инерции при вращении звена вокруг этой точки. Проведя через центр тяжести звена линию действия силы Р’и параллельно вектору ускорения выбранной точки и через центр качания линию действия силы Р» параллельно ускорению центра тяжести во вращательном движении звена вокруг выбранной точки, мы получим в точке пересечения этих линий точку, через которую
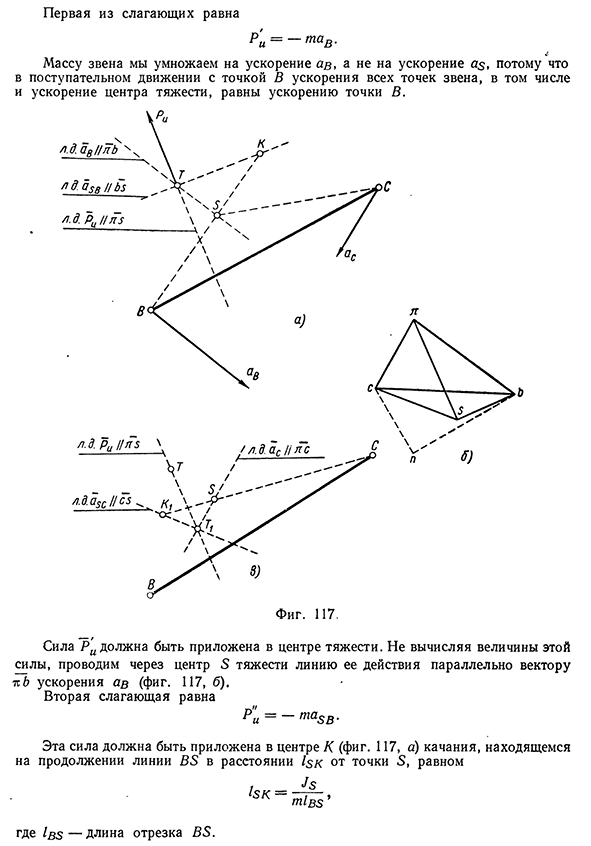
проходит линия действия полной силы Ри инерции. Вектор этой силы должен быть направлен параллельно вектору абсолютного ускорения центра тяжести в сторону, обратную направлению этого вектора. Пример 1. Звено ВС (фиг. 117, а) совершает сложное движение. Определить величину силы инерции, линию ее действия и направление по следующим данным: 1) массе пг звена; 2) моменту инерции Js звена относительно центра тяжести; 3) ускорениям ав и ас\ 4) положению центра S тяжести. По данным ускорениям ав и ас строим план ускорений (фиг. 117, б). Определив на плане ускорений положение точки s путем построения на линии Ьс треугольника bsc, подобного треугольнику BSC звена и сходственно с треугольником
BSC расположенного, получаем векторы bs и cs относительных ускорений. Проводим вектор -res абсолютного ускорения as центра тяжести. Сложное движение звена ВС рассматриваем как движение с точкой В и вращение вокруг этой точки. Полная сила Ри инерции получится в результате геометрического сложения силы инерции в движении звена с точкой В и силы Р»и инерции при вращении звена вокруг точки В.Определение сил инерции 99 Первая из слагающих равна Р’и = — тав . Массу звена мы умножаем на ускорение ав, а не на ускорение as, потому что в поступательном движении с точкой В ускорения всех точек звена, в том числе и ускорение центра тяжести, равны ускорению точки В. Сила Ри должна быть приложена в центре
тяжести. Не вычисляя величины этой силы, проводим через центр S тяжести линию ее действия параллельно вектору itb ускорения ав (фиг. 117, б). Вторая слагающая равна ?и — ~ m a SBЭта сила должна быть приложена в центре К (фиг. 117, а) качания, находящемся на продолжении линии BS в расстоянии 1$к от точки S, равном lsx = Js miss ’ где Ibs — длина отрезка BS. 7100 Кинетостатический расчёт плоских механизмов Не вычисляя величины силы Р^, проводим через центр К качания линию действия этой силы параллельно вектору bs ускорения ase-Линии действия сил Ри и Р»и пересекаются в точке Т. Для получения величины, направления и точки приложения равнодействующей Ри мы должны были бы перенести векторы этих сил по линиям их действия до точки Т, которая нами получена без вычисления длин векторов. Определив точку приложения равнодействующей Ри> вектор этой силы проводим от точки Т
параллельно и обратно вектору tcs (фиг. 117, б) абсолютного ускорения as центра тяжести. Величина Ри = —mas. Линию действия и направление силы Ри мы получили на фиг. 117, а, разложив сложное движение звена ВС на поступательное движение вместе с точкой В и вращательное движение вокруг точки В. Разлагая сложное движение звена ВС на поступательное движение вместе с точкой С и вращение вокруг точки С, центр Ki качания получаем на продолжении линии CS (фиг. 117, в) на расстоянии от центра S тяжести, равном 1ск = ^ -S K ‘ m lcs ’ Проведя через точку S линию действия ускорения ас параллельно вектору к с плана ускорений и через точку линию действия ускорения asc параллельно вектору cs, мы получим точку Т1 пересечения их на той же линии действия силы Рм, которая была получена и в предыдущем построении на фиг. 117, а. Выбрав вместо
точек В и С какую-либо иную связанную со звеном ВС точку (за исключением центра тяжести), мы получим точку пересечения линий действия сил Р’и и Р»и в новом месте, но на той же линии действия силы Ри , что и в двух предыдущих построениях. Но если движение звена ВС разложить на поступательное движение с центром тяжести и вращение вокруг центра тяжести, то все элементарные силы инерции не смогут быть приведены только к одной равнодействующей. В этом случае сила Р и = —mas = Ри должна быть приложена к центру тяжести, а сила Р получается равной нулю, так как при вращении вокруг центра тяжести элементарные силы инерции, как известно из теоретической механики, приводятся
только к паре с моментом — где е — угловое ускорение звена. Угловое ускорение е звена ВС можно определить, разложив ускорение асв (вектор вс на фиг. 117, б) на нормальное ускорение OqB (вектор Ьп на фиг. 117, б, параллельный звену ВС) и тангенциальное ускорение с?в с (вектор пс на фиг. 117, б, перпендикулярный звену ВС) и приняв во внимание, что е “ : ^вс ~ (п с ) Ра ’ ^ВС’ где — масштаб плана ускорений и 1вс — длина звена ВС. __ Направление углового ускорения выявляется в результате переноса вектора пс параллельно самому себе в точку С на фиг. 117, а\ совместив точку п вектора с точкой С на фиг. 117, а, получаем направление углового ускорения против часовой стрелки
Смотрите также:

