Определение реакций связи

Определение реакций

Обозначим через 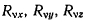проекции на неподвижные оси координат силы реакции, действующей на v-тую точку системы. Тогда уравнении равновесия каждой точки системы можно будет записать в виде

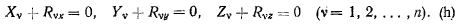
Сравнивая эти уравнения с уравнениями равновесия (е), заметим, что они совпадают, если положить

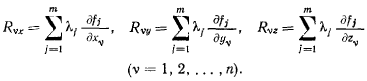
Эти соотношения можно использовать для определения реакций связи.

Рассмотрим вектор 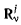с проекциями

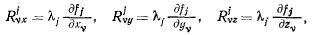
Коллинеарный вектору п нормали к поверхности

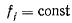
в точке 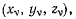причем вектор n будем считать направленным в сторону возрастания функции 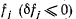(рис. 136). Вектор 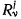будет направлен в сторону убывания функции 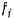и определит реакцию, действующую на v-тую точку со стороны связи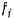

Замечание. Уравнения равновесия со множителями для освобождающих связен получены из принципа возможных перемещении при рассмотрении неосвобождающих перемещений. Эти уравнении определяют как положение равновесия, так и реакции связен. Поэтому реакции односторонних связей могут быть всегда найдены в предположении, что связи являются двусторонними.

Пример:

Исследовать условия равновесия шара на гладком горизонтальном полу, принимая последний за одностороннюю связь.

Решение:

Уравнение равновесия с множителями имеет вид

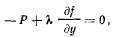
связь может быть задана условием 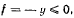поэтому

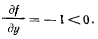
Отсюда реакция связи определяется однозначно

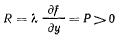
и направлена вверх.

Пример:

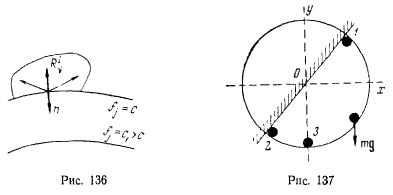
Исследовать равновесие тяжелой материальной точки, на которую наложены связи (рис. 137),

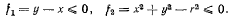
Решение:

Из принципа возможных перемещении имеем

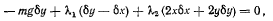
откуда, приравнивая нулю коэффициенты при 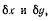получим

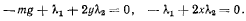
Сначала рассмотрим случай, когда в натянутом состоянии находятся обе сняли (положения 1 и 2). Тогда из уравнений связи будем иметь

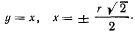
Подставляя эти значения в уравнения равновесия, получим

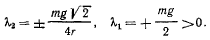
Но такие значения 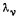не могут соответствовать положениям равновесия (в положении равновесия все 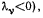следовательно, при натянутых связях положений равновесия не существует.

Если в натянутом состоянии находятся только связь 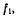то уравнения равновесия становятся противоречивыми:

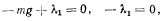
т. е. и в этом случае положения равновесия не существует.

Если же оказывается натянутой только связь 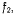то уравнения равновесия

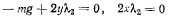
будем иметь решение

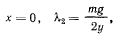
причем ?ч принимает отрицательное значение лишь при 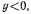т. е. возможно только одно положение равновесия (положение 3)

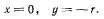
Пример:

Материальная точка с массой т находится внутри трехосного эллипсоида с полуосями a, b и с. На точку действует сила тяжести, параллельная оси г, и сила отталкивания от оси’г, пропорциональная расстоянию точки от этой осн. Найти положения равновесия точки.

Решение:

Уравнение связи запишется в виде

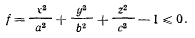
Из принципа Бернулли имеем

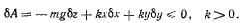
Дифференцируя уравнение связи

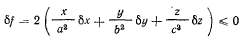
и применяя метод множителей Лагранжа, получим

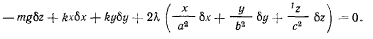
Отсюда сразу получаем уравнения равновесия:

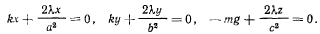
Присоединяя сюда уравнение связи, найдем следующие решения:

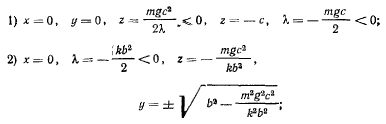
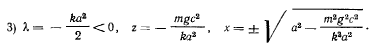
Пторое и третье решения существуют, если выполняются соответственно условия

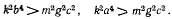
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Общие теоремы о равновесии системы материальных точек

Метод неопределенных множителей Лагранжа

Определение реакции связи в общем случае

Задача о равновесии нити