Определение реакции связи в общем случае

Определение реакции связи в общем случае

Один из способов определения реакций связей был уже рассмотрен при изучении уравнений равновесия с множителями Лаг-ранжа, когда связи задаются неявными уравнениями или неравенствами. В общем же случае связи, наложенные на систему материальных точек, всегда могут быть заменены соответствующими силами реакций, действие которых эквивалентно действию связей. После такой замены система может рассматриваться как свободная от связей, но подверженная действию как активных, так и пассивных сил. Принцип Бернулли для такой свободной системы дает необходимые и достаточные условия равновесия в виде уравнения

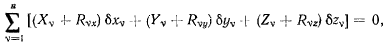
где 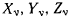— проекции активных сил на неподвижные оси координат; 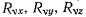— проекции сил реакции на те же оси. Величины 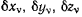теперь полностью произвольны, так что равенство (а) будет выполняться для всех возможных перемещений лишь в том случае, когда обращаются в нуль все коэффициенты при 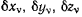т. е.

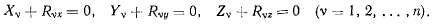
Последние уравнения и служат для определения реакций связи. Если по условиям задачи требуется определять не все, а лишь некоторые силы реакции, то система освобождается только от тех связей, реакции которых необходимо определить. Освобождая систему от связей, тем самым добавляем ей возможные перемещения, которые раньше не допускались связями и на которых будут работать реакции освобожденных связей. Подсчитывая сумму работ активных сил и сил реакции связей на освобожденном перемещении, получим условия для определения реакций связи.

Пример:

Исследовать условия равновесия твердого тела, у которого закреплены две точки 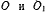и на которое действуют активные силы 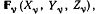приложенные к точкам 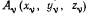(рис. 138).

Решение:

Выберем начало неподвижной системы координат в точке О. а ось z направим по прямой 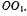Наложенные связи допускают вращение твердого тела вокруг оси z. Подсчитывая работу активных сил на этом возможном перемещении, получим

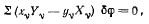
где 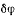— угол поворота твердого тела вокруг оси z. Отсюда сразу же получаем условие равновесия твердого тела, которое сводится к равенству нулю суммы моментов всех активных сил, действующих на твердое тело, относительно оси z:

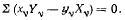
Для определения реакции в точке 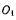освободим твердое тело от связи в этой топке; заменив действие последней действием неизвестной силы 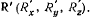Освобожденное or связи тело может вращаться как вокруг оси х, так и вокруг оси у. Сообщим твердому телу бесконечно малое возможное перемещение, повернув его вокруг оси x: на угол 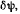подсчитаем работу всех сил на этом возможном перемещении. Возможные перемещения точек твердого тела определятся из матрицы

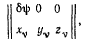
так что

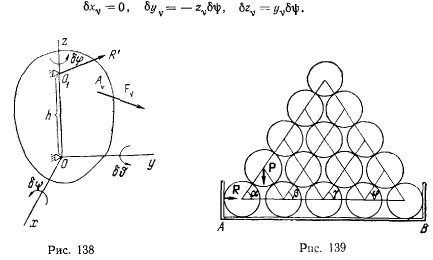
Из принципа Бериулли для освобожденного твердого тела будем иметь

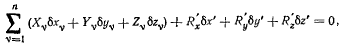
подставляя сюда Значения вариаций координат, получим

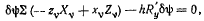
или, после сокращения на

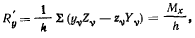
где 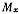—сумма моментов активных сил относительно оси а h —расстояние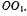

Точно таким же путем можно получить реакцию 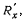рассматривая поворот твердого тела вокруг оси у. Возможные перемещения в этом случае будут определяться из матрицы

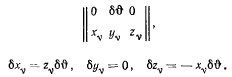
Подставляя найденные значения вариаций координат в обшее уравнение статики, получим

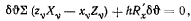
или

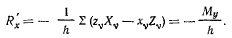
Реакция 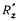таким способом не может быть найдена, потому что любое возможное перемещение точки 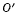твердого тела ортогонально направлению силы 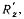и задача оказывается статически неопределимой.

Пример:

На гладкой горизонтальной плоскости лежат несколько одинаковых однородных цилиндрических труб. Чтобы трубы не раскатывались, они подпираются двумя брусьями А и В, как показано на рис. 139. Определить реакции брусьев.

Решение:

Для определенности рассмотрим пятнадцать труб, расположенных, как указано на чертеже. Чтобы избежать рассмотрения статически неопределимой задачи, предположим, что расстояние между брусками А и В больше суммы диаметров нижних труб. Положение системы «определим четырьмя параметрами 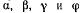которые образуют прямые, соединяющие центры труб нижнего и верхнего ряда с горизонталью), которые связаны соотношением

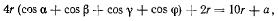
где 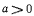— сколь угодно малое число. Углы 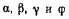подчиняются еще условиям

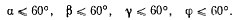
Будем предполагать сначала, что последние условия выполняются лишь в виде неравенств. Определив вертикальные координаты центров труб

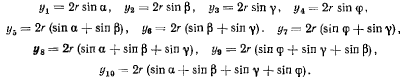
Запишем принцип Торричелли для системы с удерживающими связями:

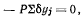
кли, после подстановки значений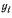

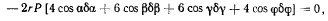
где величины 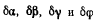связаны соотношением

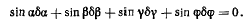
Определив из последнего уравнения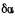

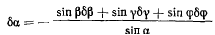
и подставив это значение в равенство (с), получим уравнение для независимых параметров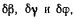

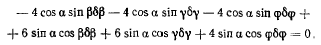
Приравнивая нулю коэффициенты при 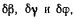приходим к следующим условиям равновесия системы:

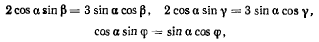
которые можно переписать в виде

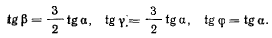
Принимая во внимание неравенства (b). получим условия равновесия

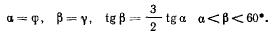
Величины а и 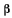должны удовлетворять уравнению (а), которое перепишется в виде

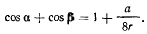
При 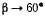отсюда находим предельное значение для а

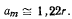
В самом деле,

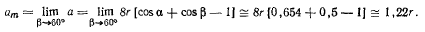
При уменьшении P левая часть равенства (f) будет увеличиваться, а следовательно, будет возрастать и а. Таким образом, предполагая связи (b) в положении равновесия выполненными в виде неравенств, устанавливаем, что в положении равновесия должно быть

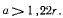
Лишь при выполнении этого неравенства нижние трубы 8 положении равновесия не будут касаться друг друга. Уменьшая а, мы вынуждены будем отказаться от предположения, что все связи (b) в положении равновесия выполняются в виде неравенств. Из условий (е) следует, что первыми переходят в равенство связи

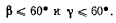
Рассмотрим теперь только такие состояния системы, для которых выполняются условия

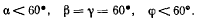
Уравнение связи для возможных перемещений (d) приобретает вид

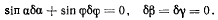
Общее уравнение статики для рассматриваемой системы перепишем в зиде

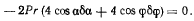
Система линейных относительно 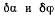уравнений (d’) и (с’) обладает ненулевым решением, если обращается в нуль определитель

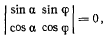
или

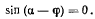
Отсюда следует, что в положении равновесия должно быть

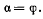
Тогда из уравнения связи (а) находим

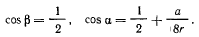
Как видно из последнею соотношения, при 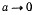получим

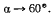
Для определения реакции в точке А, освободим систему от связи, убрав брус А и заменив его действие силой реакции R. После такого освобождения системы параметры а и 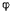можно изменять независимо друг от друга. При этом должно выполняться условие 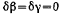(при отличных от нуля 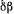или 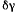системе сообщается освобождающее перемещение, на котором будут совершать отличную от нуля работу силы реакции труб, находящихся при равновесии в соприкосновении). Сообщим системе перемещение

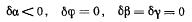
и подсчитаем работу всех сил, в том числе и работу силы R на возможном перемещении системы. Будем иметь

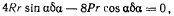
откуда следует

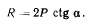
Есл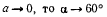и и

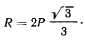
Заметим, что на рассматриваемом перемещении опускаются вниз четыре трубы. У остальных труб вертикальные координаты не изменяются. Пели обозначить через Q вес опускающихся труб (в нашем случае 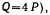то предельное значение силы реакции будет равно

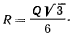
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Метод неопределенных множителей Лагранжа

Определение реакций связи

Задача о равновесии нити

Основные законы динамики