Оглавление:


Определение радиуса кривизны нейтрального слоя при прямоугольном сечении.
- Определение радиуса кривизны нейтрального слоя в прямоугольном сечении. Чтобы найти значение G, используйте следующее выражение (31.9): В случае прямоугольного поперечного сечения
стержня, это уравнение расширяется. Вызов (рис. 523) h-высота, B-ширина сечения, — радиус кривизны сердцевины—радиус кривизны внешнего волокна—
радиус кривизны внутреннего волокна, — радиус Людмила Фирмаль
кривизны G-радиус кривизны нейтрального слоя. Деление сечения на полосы dF=b dp\тогда уравнение (31.9)принимает следующий вид: Отсюда г= на » о В х (31.16) ДИСТАНЦИОННОЕ УПРАВЛЕНИЕ Rs (31.17) Формулы (31.16) и (31.17) позволяют вычислить g и G0,
а следовательно, и S для прямоугольных сечений. x) натуральный логарифм-это дробь, умноженная на 2,303.§ 1 88] определение радиуса кривизны нейтрального слоя 591 Решение может быть выполнено
- приблизительно путем разборки 1p подряд: Два. И так оно и есть. г= * О= В (31.18), В первом приближении будут ограничены первые два члена ряда.: г=Яо[1-tgl2″]’ L2 д°_127?О’ И _bh>_J12/?0_7?Ноль. — Первая и третья серии чая: G=I0[1-j L2 * о = Ио Т (31.20 утра)) (31.21) (31.18), С.- (31.22) (31.23) (31.19) Фигура. 524. L2 (31.24) Где J-момент инерции
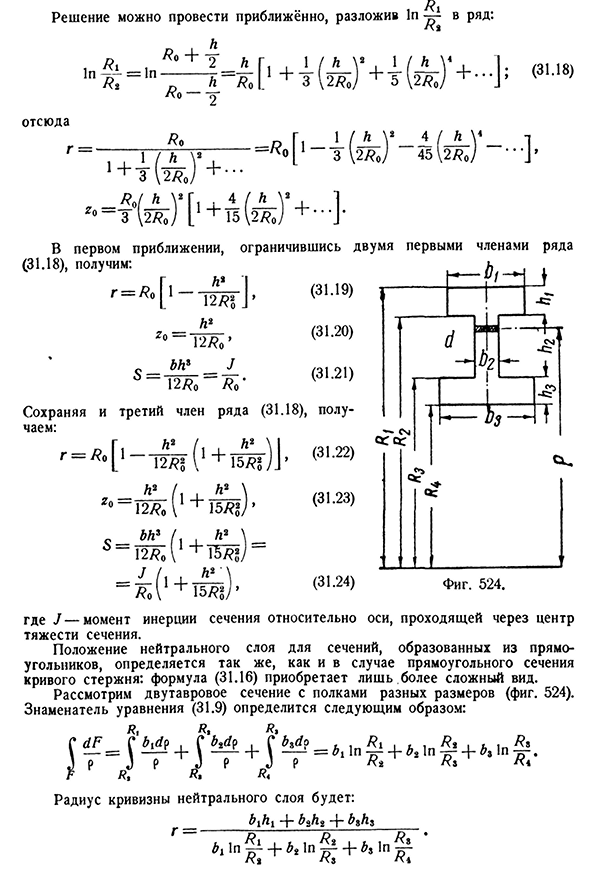
сечения относительно оси, проходящей через центроид сечения. Положение нейтрального слоя сечения, образованного прямоугольником, определяется так же, как и в случае прямоугольного сечения криволинейного стержня: формула
(31.16) приобретает только более сложные формы. Рассмотрим полки и I- Людмила Фирмаль
образные секции различных размеров(рис. 524). Знаменатель уравнения (31.9) определяется как: F Ri R. 4 радиус кривизны нейтрального слоя равен: ^ 1 ^ 1 + ^ 2 ^ 2 +
Смотрите также:

