Оглавление:

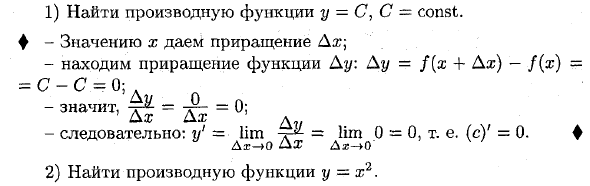


Определение производной; ее механический и геометрический смысл. уравнение касательной и нормали к кривой
- Определение производных терминов; Его механический и геометрический смысл. Уравнения касательной и регулярной кривой Предположим, вы определили функцию y = f (x) с определенным интервалом (a; 6). Выполните следующие действия: -Укажите приращение Ax: x + Да: € (a; b) для аргумента x €. ~ Найти соответствующее приращение функции: Au = = / (* + Ax) -f (x)] -Создает отношение приращения функции к приращению аргумента. -Найти границы этого отношения с Ах- »0: Иш
Производная функции y = f (x) в xq является пределом отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Так по определению = lim / (x0 + Ax) -} (xd) или = lim D *) — / Ы J-> 0 Ax * — + x0 X-. Производная функции f (x) — это функция f ′ (x)>, полученная из конкретной функции. Функция y = f (x) с производной в каждой точке интервала (a; 6) называется дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.
Когда это ограничение существует, оно называется производной функции f (x) и обозначается символом A, f ‘(x) \ y’] y’x. Людмила Фирмаль
Значение производной функции y-f (x) в точке x = x0 указывается либо символом f ‘(n0)> y’ \ _, либо y ‘(тогда). 11 — XQ Пример:1) Найти производную функции y = C, C = const. Присвойте значению -x значение Ax. — найти приращение функции Ду = f (x-f Да;) С-С = 0; & U o p -Средства -r-2 — r ^ — = и; «Да, да; D Поэтому: y ‘= lim-q-> lim 0 = 0, т. Е. (C)’ = _ g-2 2) Найти производную функции y = a.
Аргумент x указывает на инкрементальный Dx. -Лу: Ау = (х + Дх) 2-х2 = 2х • Дх + (да 🙂 2 ‘; Д ‘(/ Д-у2х • Дх + (Дх) 2 0, л -Настроить отношения -r- *: —-t — 1-— = 2a; 4-Dx; Дх Дх Да: Определите пределы этих отношений: ах lim ~ = lim (2x + Dx) = 2a; Dh- * 0 Dh Dh— »0 Следовательно, (x2) ‘= 2x. ♦ Была получена задача о скорости линейного движения V = Rela 4t D £ _ * в 0 Перепишите это уравнение в виде: V = 5J, то есть скорость линейного перемещения материальной точки в момент времени t является производной пути S по времени t.
| Свойства функций, непрерывных на отрезке | Связь между непрерывностью и дифференцируемостью функции |
| Задачи, приводящие к понятию производной | Производная суммы, разности, произведения и частного функций |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Это механическое значение производства. Таким образом, если функция y = f (x) описывает физический процесс, то производная y ‘является скоростью этого процесса. Это физический смысл производной. Коэффициент касательного угла k = tgr * = был найден для задачи касательной кривой.
Это геометрическое значение дифференциации. Если координаты контакта M (xo; 2 / o)>, коэффициент угла касания равен k = /; (xo). Вы можете написать уравнение касательной, используя линейное уравнение через заданную точку в заданном направлении (y-2 / o = k (x-yo)):
Перепишите это уравнение В виде f ‘(x) = tga = k, то есть производная f’ (x) в точке x является угловым коэффициентом касательной к графику функции y = / (x) в точке, где абсцисса равна x Людмила Фирмаль
Y-yo / s) — (х-хо). Линия, перпендикулярная касательной в точке контакта, называется кривой нормали. Поскольку нормаль перпендикулярна касательной, ее угловой коэффициент L-HOpM. «Муть. 1 / ‘S’ в \ а Вы есть Следовательно, форма нормального уравнения имеет вид y-yo = (если f ‘(xo) Φ0). (Х-Хо) Ваш «

