Оглавление:
Определение прогибов и углов поворота в балках методом начальных параметров
Если балка постоянной жесткости EJ и имеет несколько участков, то удобнее прогибы и углы поворота определять по методу начальных параметров. Возьмем приближенное дифференциальное уравнение
d2V Мх
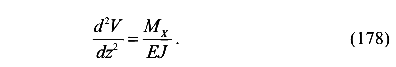
Учтем, что производная от прогиба равна углу поворота

Поэтому уравнение (178) можно записать в следующем виде
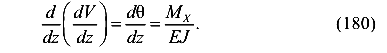
Разделим дифференциалы

Проинтегрируем левую и правую части уравнения

или
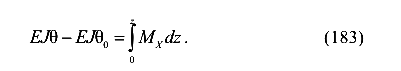
В уравнении (183) перенесем 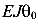 в правую часть
в правую часть
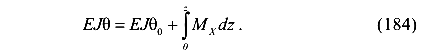
Далее выразим угол поворота через прогибы
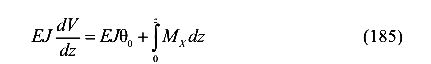
или
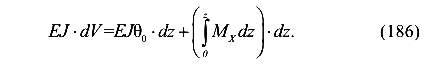
Проинтегрируем левую и правую части уравнения
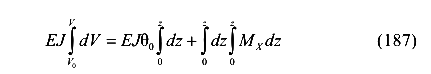
или
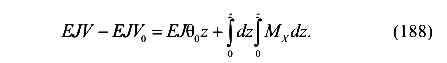
Перенесем 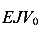 в правую часть уравнения (188) и получим
в правую часть уравнения (188) и получим
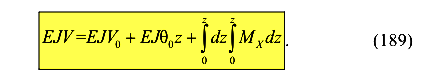
Получена интегральная форма функции прогибов балки (189).
Здесь 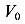 и
и 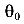 — начальные параметры. На основе полученной зависимости строится метод начальных параметров.
— начальные параметры. На основе полученной зависимости строится метод начальных параметров.
Для взятия интеграла в уравнении (189) от отдельных наиболее часто встречающихся видов нагрузок рассмотрим балку, загруженную одним сосредоточенным моментом, одной сосредоточенной силой и одной равномерно распределенной нагрузкой (рис.64). Обозначим координаты точек приложения сосредоточенного момента и сосредоточенной силой,
соответственно, 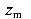 и
и 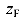 Координата начала участка приложения равномерно распределенной нагрузки обозначим
Координата начала участка приложения равномерно распределенной нагрузки обозначим 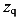 .
.
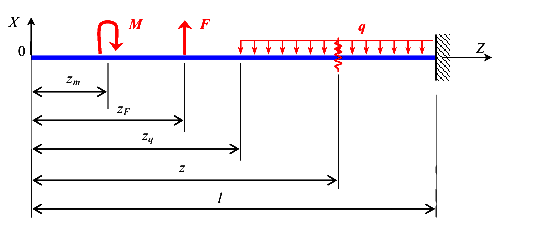
Возьмём интеграл ,содержащийся в уравнении (189)
-от сосредоточенного момента 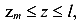
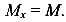
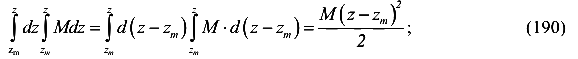
-от сосредоточенной силы 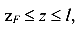
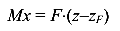
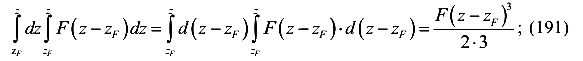
-от распределенной нагрузки 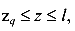
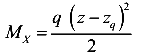
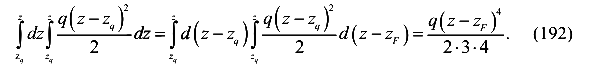
Суммируя интегралы от всех видов нагрузок и полагая, что к балке могут быть приложены несколько нагрузок одного и того же вида, получим универсальное уравнение упругой оси балки.
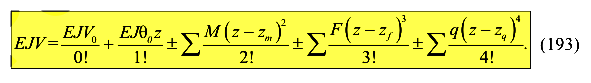
Преимущества метода начальных параметров заключается в том, что нам приходится находить только две постоянные интегрирования. Особенно это преимущество заметно, если на балке несколько участков. Однако, метод начальных параметров имеет и недостатки — балка должна быть постоянной жесткости на всей ее длине; слагаемые в универсальном
уравнении упругой оси балки могут отличаться на порядки (193). Поэтому при использовании метода начальных параметров предъявляются определенные требования.
Правила и требования:
1) Начало координат всегда выбирать в левой крайней точке балки.
2) Начальные параметры равны соответственно прогибу и углу поворота сечения на левом конце балки.
3) При вычислении прогибов или углов поворота сечения балки учитывать только слагаемые, содержащие силовые факторы, приложенные левее рассматриваемого сечения.
4) Знак перед слагаемым совпадает со знаком изгибающего момента в рассматриваемом сечении, вызванного силовым фактором, содержащимся в этом слагаемом.
5) Где-то начавшаяся равномерно распределенная нагрузка не должна заканчиваться до правого конца балки.
Уравнения углов поворота получается взятием производной от уравнения для прогибов (200).
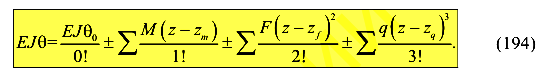
Правило знаков:
Прогиб вверх и поворот против хода часовой стрелки считаются положительными.
Пример:
Определение прогибов в балке методом начальных параметров (рис.65, а).
Подготовим балку согласно требованиям метода начаоьных параметров: начало координат поместить в левой крайней точке балки; продольную ось направить вправо; ось V направить вверх; пронумеровать участки балки слева направо; дополнить нагрузку q и приложить компенсирующую нагрузку q снизу вверх (рис. 65, б).
Вычислим реакции опор
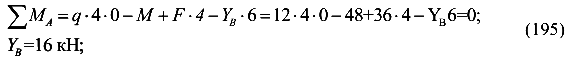
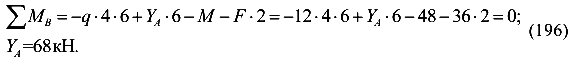
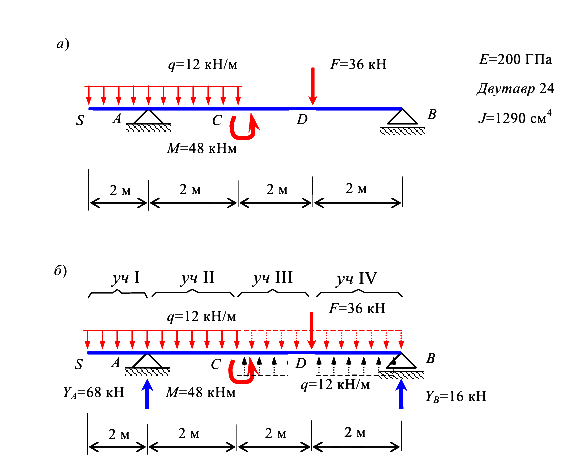
Составим универсальное уравнение упругой оси балки
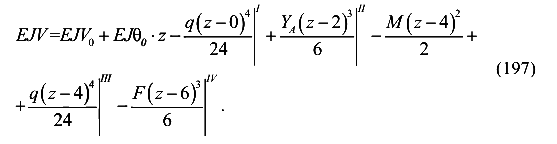
По условию закрепления определим начальные параметры
1) На опоре A z = 2 м, участок I V=0.
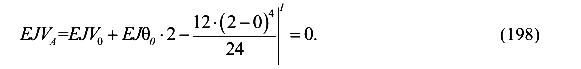
2) На опоре В z = 8 м, участок III V=0.
12-(8-О)4
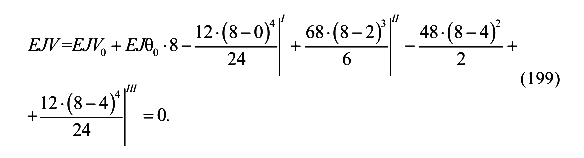
Выполним вычисления и получим два уравнения с двумя неизвестными 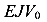 и
и 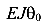 .
.
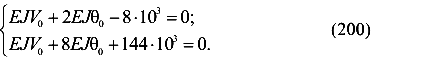
Решим систему и получим начальные параметры
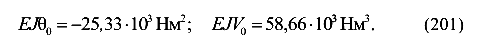
Вычислим прогиб в точке S (z = 0, участок I)
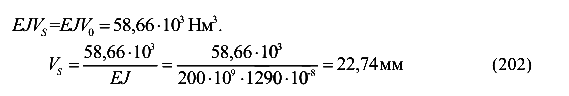
Подставляя данные в выражение (203) вычислим прогиб в точке D (z = 6 м, участок III)

Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Дифференциальное уравнение изогнутой оси балки |
| Метод непосредственного интегрирования |
| Напряженное и деформирование состояние в точке |
| Правила расстановки индексов и знаков |

