Определение прогибов балки при плоском и пространственном косых изгибах
Вначале получим выражения для прогиба консольной балки, загруженной сосредоточенной силой (рис.115). Для вычисления прогибов воспользуемся методом Максвелла-Мора.
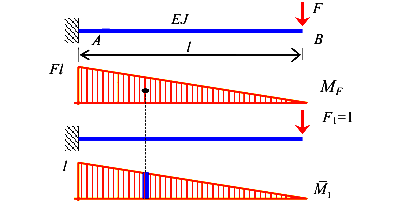
В результате получим прогиб в точке В
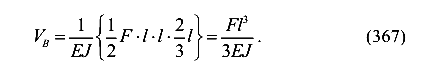
Косой изгиб разделяют на два вида — плоский и пространственный. Косой изгиб называется плоским, если упругая ось балки является плоской кривой.
Косой изгиб называется пространственным, если упругая ось балки является пространственной кривой.
Рассмотрим плоский косой изгиб (рис.116).
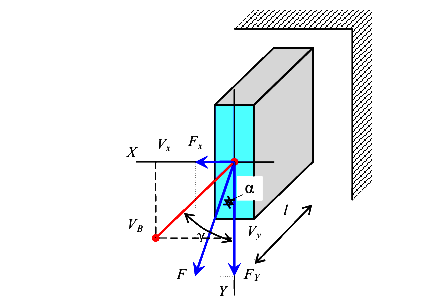
Учитывая принцип независимости действия сил, найдем прогибы от составляющих сил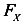 
и 
.
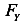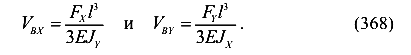
Полный прогиб равен геометрической сумме прогибов в вертикальном и в горизонтальном направлениях
Определим направление полного прогиба балки в точке В
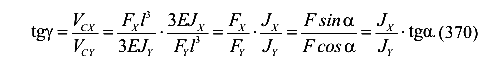
Окончательно имеем
Так как
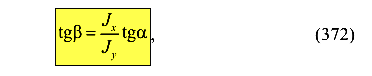
то есть углы равны друг другу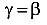 
. Но углы откладываются от взаимно перпендикулярных осей X и Y, поэтому направление полного прогиба при плоском косом изгибе перпендикулярно нейтральной оси.
Вместе с тем, отметим, что при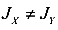 
направление полного прогиба не совпадает с направлением действия силы 
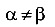. Это и послужило причиной назвать этот вид сопротивления косым изгибом. И действительно сила действует в одном направлении, а полный прогиб направлен в другом.
Для пространственного косого изгиба положение, то есть угол a, плоскости действия суммарного изгибающего момента для различных сечений балки разное и зависит от значений изгибающих моментов в нем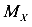 
и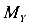 
.
Поэтому для определения полного прогиба балки и его направления необходимо найти прогибы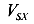 
и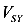 
рассматриваемом сечении S по направлениям главных осей инерции X и У отдельно, а затем их геометрически сложить. При этом прогибы определяются по общим правилам для плоского простого изгиба.
Направление полного прогиба в сечении S можно установить по его проекциям
Примечание. Чтобы установить какой вид косого изгиба испытывает балка не обязательно строить ее упругую ось и увидеть, что она плоская или пространственная. Тем более, что это очень трудоемко и сложно. Достаточно лишь установить, что отношение моментов
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
