Определение предела

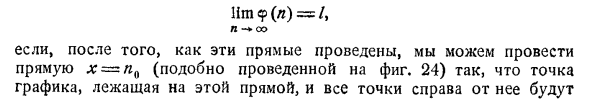
Определение предела

• Определение предела. После каждого обзора читатели должны понимать общую концепцию ограничений. Грубо говоря, 9 (η) является I-пределом η-vω, если 9 (π) приблизительно равен I, когда η велико. Однако значение этого описания должно быть достаточно ясным уже после всего вышеперечисленного, но тем не менее этого достаточно для точного математического определения, которое мы его сформулировали. Не является точным.

Это утверждение должно встречаться для всех значений n, начиная с определенного значения n0 (8), для 8 = 0,001 или 0,0001 или положительного числа, и для каждого такого значения 8, В принципе, чем меньше значение 8, тем больше соответствующих значений nn (o). Таким образом, можно сформулировать следующее окончательное определение: Однако, если положительное число 8 мало, число n0 (o), соответствующее этому 8, устанавливается так, чтобы 9 (n) отличалось менее чем на 8 для всех значений n, больших или равных n () (o)

Фактически, приведенное выше утверждение соответствует всему классу операторов типа «n 9 (n) отличается от I менее чем на 8». Людмила Фирмаль

Могу найти Положительная разница между 9 (?) А / обычно обозначается как | 9 (г) -. Два числа 9 (n) — /, равные I-9 (//), равны определению модуля 9 (//) — / second. III. На данный момент учитываются только положительные или отрицательные значения. Применяя это обозначение, мы можем формализовать определение следующим образом: для любого небольшого положительного числа b и n0 (8) отображается как | 9 (l) -9 (l) требуется Предел I, где п, как правило, со lim 9 (/ г) = A и Изредка опускайте «p —ooh *;». Для краткости полезно написать y (l) — /.

Для читателя полезно вычислить явное выражение как 0 как функцию от & в некоторых простых случаях. Следовательно, p (x) = -, / = 0, и условие удовлетворен, если f0 = I + j- + j 5 n и менее 5 о какие N N у-1> д Если один и тот же n0 подходит для всех значений 5, существует только один. Начиная со значения N, если и всех положительных значениях 5. С другой стороны, для Ы и всех положительных значений 6, N. Следовательно, (n) постоянна для всех таких значений n. 59. Определение ограничения можно описать геометрически следующим образом: Граф <p (n) состоит из ряда точек, соответствующих значениям n = 1, 2, 3, …. Нарисуйте прямую линию y = 1 (рис. 24) и линию, параллельную ей, на расстоянии 6 от y = zl- ^ = / -j-. тогда lim 9 (l) = /, с н После того, как эти линии нарисованы, нарисуйте линию x = nn (аналогично линии, изображенной на рисунке 24) и точки на графике над этой линией и все точки справа

• Решение задач по высшей математике

Выражение „n стремится к бесконечности»	Колеблющиеся функции
Поведение функции от n когда n стремится к бесконечности	Функции от n, монотонно возрастающие вместе с n

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Между ними. Эта геометрическая интерпретация определения оказывается особенно полезной при рассмотрении функций, определенных для всех значений действительных переменных, а не только положительных целочисленных значений. Вышесказанное достаточно для функций, которые стремятся к пределам, таким как 60.η-> ∞. Вы должны перейти к соответствующему определению функции, которая имеет тенденцию быть положительной или отрицательной бесконечностью, такой как «я» или «я».

Следующие определения не должны вызывать проблем у читателя. Определение II. ); Это означает, что независимо от того, насколько велико D, 9 (s)> D для достаточно большого значения n. «9 (i) Когда я могу увеличить произвольно большое I». Эта формулировка не полностью подчеркивает основные положения определения. То есть 9 (i) должно быть больше D для всех значений n. Вы также можете применить эту форму выражения, если вы знаете ее значение, а не только для таких значений, как I ^ i0 (D). 9 (I) Если мы стремимся к оо, 9 (n) — * ~ g Вы можете предоставить читателям соответствующий язык определения для функций, которые имеют тенденцию быть отрицательной бесконечностью.

Функция 9 (π) способна показать η0 (), так что cp (n)> A для всех независимо от того, насколько велико данное число Δ Людмила Фирмаль

Некоторые комментарии к определению. Читатели должны знать следующее: (1) Очевидно, что n имеет тенденцию быть ω, поэтому значение <p (n) может быть установлено любым конечным числом n любым способом, не влияя на поведение ep (n). Вы можете изменить это. Например ~ Имеет тенденцию быть 0, и n имеет тенденцию быть co. Может сделать из любого числа новых функций, меняя их конечное число значений. Таким образом, функцию ((λ) можно считать равной 3 при / 2 = 1, 2, 7, 11, 101, 107, 109, 237 и равной всем другим значениям n. Эта функция И lim (n) = 0 исходной функции I. Аналогично, для функции ep (n) n = 1, 2, 7, 11, 101, 107, 109, 237 равно 3, и все Если n}, оставшееся значение равно 2: 9 (i) — * — ω,

(2) С другой стороны, как общее правило, если n имеет тенденцию быть со, его бесконечное значение с без фундаментального изменения его поведения? (L) не может быть изменено. Например, если вы измените Функция-, всегда устанавливайте значение 1 для n Если оно кратно 100, соотношение lim

237, но на самом деле, если фиктивный враг (56) имеет значение 8, меньше 3 (в первом примере), а D имеет большое значение, то 3 Вот и все (второй пример). Но теперь, независимо от того, насколько велико ln, значение l всегда увеличивается при изменении 9 (n). (3) При применении атрибутов определения I необходимо убедиться, что оно применяется не только к неравенству [9 (π) -η = 00, но также ко всем большим значениям n0 и n. Например, k) является функцией, рассматриваемой в (2), и, если задано 8, можно найти n0, потому что 19 (/ *); <[8 для n = nQ: для этого n0 Должен быть выбран достаточно большим, а не кратным 100.

Однако, если вы выберете n0, неравенство | 9 (x) | <^ 8 ^ 1 является исключением для r> 100. (4) Если 9 (l) всегда больше / можно просто заменить | 9 (н) -9 х (/ г) — /. Следовательно, когда η имеет тенденцию быть oo, тенденция к пределу 0 является только справедливостью неравенства -i 8 для η> η (). Однако 9 (/ r) = (-1) «~ t Я все еще 0, но 9 (l) — / иногда положительный, а иногда отрицательный. В этом случае условие должно быть сформулировано в виде 19 (n) — / {8. В этом случае особенно 19 (n) | 8. (5) Само ограничение I является одним из принятых значений для 9 (n). Поэтому ясно, что lim9 (β) = 0, если 9 (Λ) = 0 для всех значений n.

Другой пример: если вы хотите изменить значение функции для всех значений, как в (2) и (3) / g, кратное 100, но 0 вместо 1 и 9 равно 0 (/ g) прибудете Это ограничение, если n кратно 100, а оставшееся значение n равно Функция, где n имеет тенденцию быть oo, равна 0 и получается функцией для всех бесконечных значений n, то есть кратных 100. С другой стороны, предел не должен быть одним из значений, принятых функцией (обычно нет) 1C $ любой имеет значение lib n.

Это Здесь предел равен 0, но функция не равна 0 для значения i. Читатели не могут переоценить важность этих фактов. Предел не является значением функции. Это может быть определено этими значениями, но они могут отличаться. Для функции <p (/ z) = 0 или 1 предел равен всем значениям функции 9 (l). для , <«) = I, (-1 г-л, 1 + JL, i + (-i)» i Не равно ни одному значению в функции. для .1 .1 Sin-PC SUl- ^ / 2 * —s— «X + (Предел имеет тенденцию быть ω для ясности, поэтому sin-πmodulo не превышает 1, поэтому он равен 0 и 1 соответственно.)

Предел равен 9 (для всех четных значений l l) равно значению, которое принимается, но принимается функцией для нечетных значений l, отличающихся от предельного значения. (6) Если л очень большой, функция будет очень большой, но — {- ко или ко-ко. Хорошим объяснением этой ситуации является функция 9 (n) = (-1) n. Функция имеет тенденцию быть -} — co или k-co. Только если начать с определенного значения l и сохранить знак.