Оглавление:
Определение положения центра тяжести фигур и тел сложной формы
Аналитический способ
Для определения положения центра тяжести фигур и тел сложной геометрической формы их мысленно разбивают на такие части простейшей формы (если, конечно, это возможно), для которых положения центров тяжести известны. Затем определяют положение центра тяжести всей фигуры или тела по формулам § 39, понимая в этих формулах под 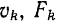 и
и 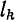 объемы, площади и длины частей, на которые разбито данное тело, фигура или линия, а под
объемы, площади и длины частей, на которые разбито данное тело, фигура или линия, а под 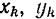 и
и 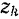 — координаты центров тяжести этих частей.
— координаты центров тяжести этих частей.
Если рассматриваемые фигуры или тела неоднородны, то, разделив их па однородные части, умножают входящие в формулы (43), (44) и (47) объемы, площади и длины этих частей на соответствующий каждой части удельный вес. Если в данном теле или фигуре имеются полости или отверстия, то для определения центра тяжести такого тела или фигуры пользуются теми же приемами и формулами, считая при этом объемы и площади вырезанных частей отрицательными.
В тех случаях, когда данное тело нельзя разбить на такие части, для которых было бы известно положение их центров тяжести, для вычисления координат центра тяжести тела приходится пользоваться методами интегрального исчисления.
Экспериментальный способ
Для определения центра тяжести неоднородных тел сложной формы существуют различные экспериментальные методы. Рассмотрим на примерах два из них.
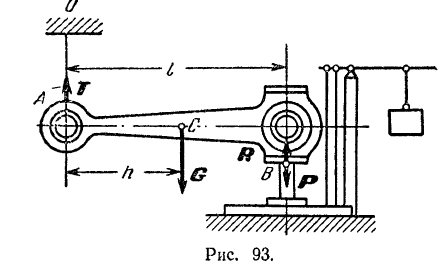
I. Метод взвешивания. Для определения положения центра тяжести шатун 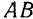 (рис. 93) подвешиваем в точке
(рис. 93) подвешиваем в точке 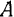 и опираем точкой
и опираем точкой 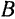 на платформу десятичных весов, так чтобы он занял горизонтальное положение. Сила давления шатуна на платформу, найденная путем взвешивания, оказалась равной по модулю
на платформу десятичных весов, так чтобы он занял горизонтальное положение. Сила давления шатуна на платформу, найденная путем взвешивания, оказалась равной по модулю 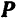 . К находящемуся в равновесии шатуну приложены силы: сила
. К находящемуся в равновесии шатуну приложены силы: сила 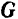 тяжести шатуна, проходящая через его центр
тяжести шатуна, проходящая через его центр 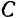 тяжести, вертикальная реакция
тяжести, вертикальная реакция 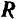 платформы, проходящая через точку
платформы, проходящая через точку 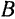 и равная по модулю силе
и равная по модулю силе 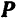 давления шатуна на платформу, и сила
давления шатуна на платформу, и сила 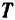 натяжения нити
натяжения нити 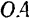 .
.
Зная вес 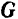 шатуна и расстояние
шатуна и расстояние 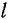 между его точками
между его точками 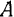 и
и 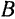 , теперь нетрудно найти и расстояние
, теперь нетрудно найти и расстояние 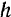 от точки
от точки 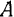 до центра
до центра 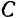 тяжести шатуна. Одним из уравнений равновесия шатуна будет:
тяжести шатуна. Одним из уравнений равновесия шатуна будет:
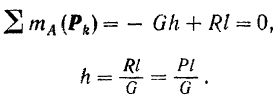
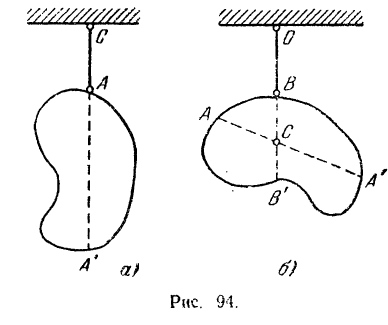
- Метод подвешивания. Тело подвешивают на нити за какую-либо его точку
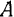 (рис. 94, а) к неподвижной точке
(рис. 94, а) к неподвижной точке 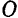 . После того как тело придет в равновесие, проводят вертикальную линию
. После того как тело придет в равновесие, проводят вертикальную линию 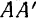 , составляющую продолжение направления нити
, составляющую продолжение направления нити 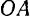 . При равновесии центр тяжести тела должен находиться на одной
. При равновесии центр тяжести тела должен находиться на одной
вертикали с неподвижной точкой 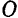 и, следовательно, будет лежать на линии
и, следовательно, будет лежать на линии 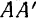 . Вновь подвесив тело к другой его точке
. Вновь подвесив тело к другой его точке 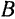 (рис. 94,6), мы точно так же найдем, что его центр тяжести лежит на линии
(рис. 94,6), мы точно так же найдем, что его центр тяжести лежит на линии 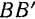 , являющейся продолжением направления нити
, являющейся продолжением направления нити 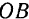 . Точка
. Точка 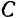 пересечения линий
пересечения линий 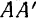 и
и 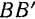 и будет являться центром тяжести тела. Способ подвешивания удобен для определения положения центра тяжести тонких пластинок.
и будет являться центром тяжести тела. Способ подвешивания удобен для определения положения центра тяжести тонких пластинок.
Пример задачи:
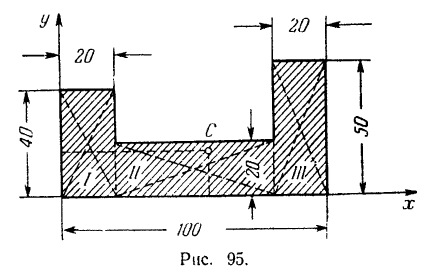
Найти статические моменты относительно координатных осей площади листа и координаты его центра тяжести. Размеры листа (в сантиметрах) указаны на рис. 95.
Решение:
Разобьем данную площадь на три прямоугольника. Центр тяжести каждого из прямоугольников лежит на пересечении его диагоналей. Координаты этих центров, так же как и площади прямоугольников, легко определяются из чертежа.
По формулам (45) находим статические моменты площади данной фигуры
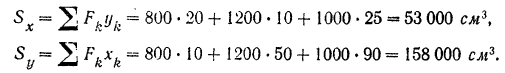
Определяем теперь по формулам (46) координаты центра тяжести площади фигуры:
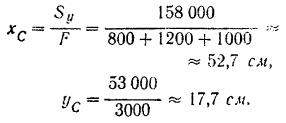
Пример задачи:
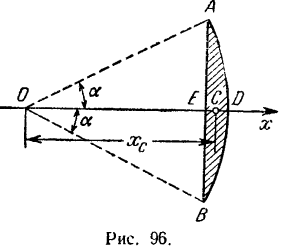
Найти центр тяжести 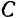 площади кругового сегмента
площади кругового сегмента 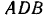 радиуса
радиуса 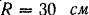 , если
, если 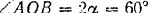 (рис. 96).
(рис. 96).
Решение:
Искомый центр тяжести 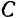 лежит на оси симметрии, проходящей через центр круга
лежит на оси симметрии, проходящей через центр круга 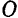 и середину
и середину 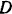 дуги
дуги 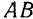 . Направим вдоль прямой
. Направим вдоль прямой 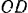 ось
ось 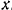 . Начало координат возьмем в точке
. Начало координат возьмем в точке 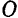 Будем рассматривать круговой сегмент как состоящий из двух фигуp: кругового сектора
Будем рассматривать круговой сегмент как состоящий из двух фигуp: кругового сектора 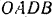 и треугольника
и треугольника 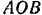 , причем вторую площадь надо считать отрицательной.
, причем вторую площадь надо считать отрицательной.
Площадь кругового сектора
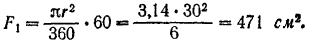
Абсцисса его центра тяжести
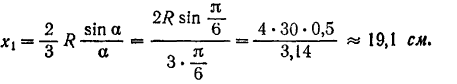
Площадь треугольника
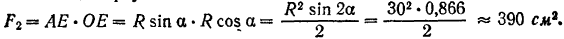
Абсцисса его центра тяжести
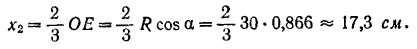
По формуле (44) определяем абсциссу центра тяжести данного кругового сегмента:
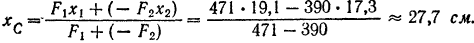
Пример задачи:
Тело состоит из деревянного цилиндра II, радиус которого 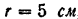 высота
высота 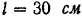 и двух скрепленных с ним стальных шаров I и III с радиусами
и двух скрепленных с ним стальных шаров I и III с радиусами 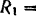
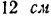 и
и 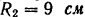 (рис. 97). Определить положение центра тяжести этого тела, если удельный вес дерева
(рис. 97). Определить положение центра тяжести этого тела, если удельный вес дерева 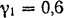 и удельный вес стали
и удельный вес стали 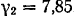 .
.
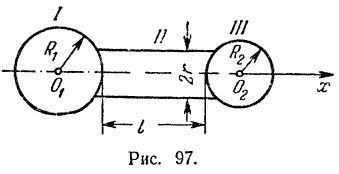
Решение:
Искомый центр тяжести лежит на оси симметрии, проходящей через центры шаров 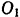 и
и 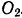 . Начало координат возьмем в центре
. Начало координат возьмем в центре 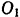 большого шара и ось симметрии примем за ось
большого шара и ось симметрии примем за ось 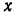 . Разобьем тело на три части и составим для них таблицу объемов и координат (абсцисс) центров тяжести.
. Разобьем тело на три части и составим для них таблицу объемов и координат (абсцисс) центров тяжести.

Для определения абсциссы центра тяжести всего неоднородного тела воспользуемся формулой (42):
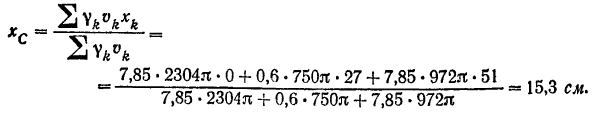
Пример задачи:
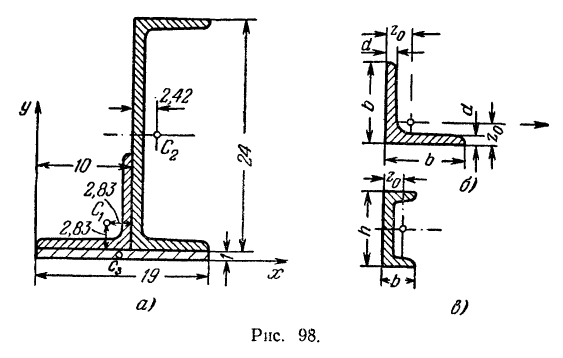
Определить статические моменты относительно координатных осей и положение центра тяжести сечения (рис. 98, я), составленного из равнобокого уголка 100 X 100 X 10, швеллера №24 и полосы 190 X 10.
Решение:
Из таблиц нормального сортамента для прокатной стали ‘) выпишем следующие данные:
I. Равнобокий уголок (рис. 98,6), ГОСТ 8509-57. Профиль № 10. Ширина полки 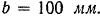 Толщина полки
Толщина полки 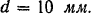 . Площадь поперечного сечения
. Площадь поперечного сечения 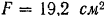 Расстояние центра тяжести от оснований полки
Расстояние центра тяжести от оснований полки 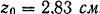 .
.
II. Швеллер (рис. 98, в), ГОСТ 8509-57. Профиль № 24. Высота стенки 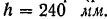 Ширина полки
Ширина полки 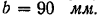 Толщина стенки
Толщина стенки 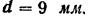 Площадь поперечного сечения
Площадь поперечного сечения 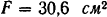 . Расстояние центра тяжести от наружного края вертикальной стенки
. Расстояние центра тяжести от наружного края вертикальной стенки 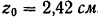 . (Швеллер имеет горизонтальную ось симметрии и, следовательно, его центр тяжести лежит на этой оси.)
. (Швеллер имеет горизонтальную ось симметрии и, следовательно, его центр тяжести лежит на этой оси.)
III. Полосовая сталь, ГОСТ 103-57. Сечение — прямоугольник. Ширина полосы 190 мм. Толщина 10 мм. Площадь поперечного сечения 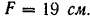
Нумеруем отдельные части сечения и на основании записанных выше данных проставляем соответствующие размеры (в см) на рис. 98, а. Оси координат выбираем так, как указано на этом рисунке.

Статический момент сечения относительно оси 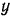 :
:
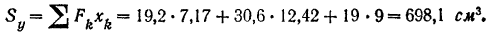
Статический момент сечения относительно оси 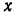 :
:
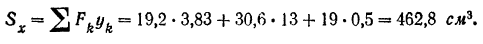
Координаты центра тяжести сечения:
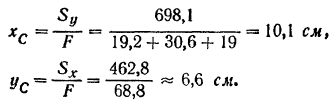
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

