Оглавление:














Определение перемещений в балках по методу начальных параметров
- Определение смещения балки Кстати о начальных параметрах Определение перемещений путем прямого интегрирования дифференциальных уравнений упругих линий в случае балок с большим числом сечений сопряжено со значительными трудностями. Эти трудности заключаются не в интегрировании дифференциальных уравнений, а в методике определения какой-либо интегральной постоянной, представляющей собой составление и решение системы линейных алгебраических уравнений. Поэтому, если балка в условиях нагрузки разделена на n участков, то Интеграл дифференциальных уравнений для всех участков балки добавляется к двум основным опорным условиям любой балки 2 (l-1) из 2P,
а условия сопряжения всех участков упругой линии используются для определения этих констант.、 Задача уже будет очень трудоемкой с n=3. Для сокращения больших вычислительных задач, связанных с определением произвольных интегральных констант, было разработано несколько методов. К ним относится метод начальных параметров, позволяющий на любом количестве участков свести решение к нахождению только двух констант-отклонения и угла поворота в начале координат. Вывод общих уравнений и примеры их применения. Рассмотрим часть длины луча / 1. 280, а),
имеющий поперечное сечение в точках K и L. 280, б показывает этот сегмент, нагруженный наиболее распространенной нагрузкой, такой как: а) Людмила Фирмаль
сосредоточенный момент сечения с горизонтальной осью M\b)имеет горизонтальную ось ()=qc+k (x-c}, где k-касательная касательная к наклону к эпюре нагрузки (рис. 280, а): Далее на концах рассматриваемой части балки прикладываются боковые силы и изгибающие моменты, которые заменяют действие мысленно покинутой части балки. При выводе уравнения направления всех нагрузок выбирайте так, чтобы они вызывали положительный изгибающий момент. Подумайте об этом как о сегменте, где у вас есть несколько концентраций времени, концентрации и т. д., И сколько вам нужно сделать, чтобы рассеять нагрузку.
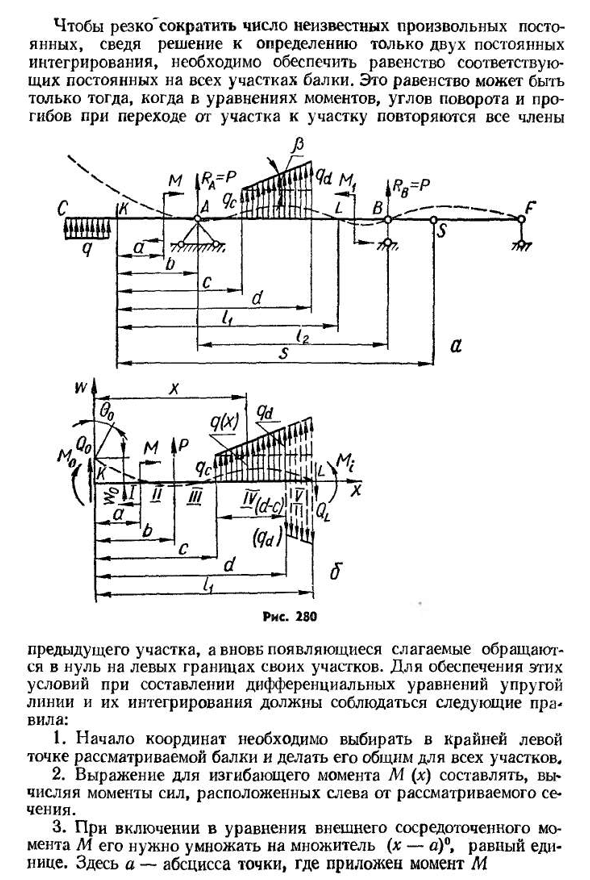
Мы показываем в луче только один из перечисленных коэффициентов мощности с целью дальнейшего упрощения расчета. 281 чтобы значительно уменьшить число произвольных констант неизвестного и уменьшить решение задачи определения двух интегральных констант, необходимо обеспечить равенство соответствующей константы во всех частях балки, причем это равенство возможно только в том случае, если все члены повторяются в уравнениях момента, степени поворота и прогиба при движении балки. Из предыдущего сюжета вновь возникающий термин исчезает на левой границе сюжета. Для обеспечения этих условий при
- построении дифференциальных уравнений упругих линий и их интегралов необходимо соблюдать следующие правила: 1. Начало координат должно быть выбрано в самой левой точке балки и сделано общим для всех секций 2. Формула для изгибающего момента 7I (x) рассчитывается путем вычисления момента силы, расположенного слева от рассматриваемого участка. 3. Если в уравнение включен внешний конденсированный момент M, то его необходимо умножить на коэффициент (x—a)°. Где A-абсцисса точки, в которой приложен момент м 2824 в случае повреждения распределительной нагрузки(например, в сечении x=d, фиг. 280, Б) В конце рассматриваемого участка для восстановления фактических условий нагрузки вводится обратная «компенсирующая» нагрузка. «Дополнительные»и» компенсирующие » нагрузки отображаются
на чертеже пунктирной линией. 5. Чтобы закрепить уравнение во всех областях, нужно обойтись без открытия скобок. Таким образом, если вы выберете начало координат в самой левой точке(точке K) рассматриваемого вами сегмента балки, вы можете использовать любой участок самого правого (V) участка в соответствии с пунктами 2-4 настоящих Правил. В этом случае условимся разделить трапециевидную нагрузку на треугольники, равномерно распределенные в них. Изгибающий момент записывается следующим образом: M(x)=M o4-Qox+M(x—a)°+P (x-b) + qc2—Yaa+k-K.(10.76)диаграмма, которая рассматривает чертеж луча (рис. 280, б), уравнение изгибающего момента IV сечения легко получается из уравнения (10.76), и его легко снять с учетом нагрузки, возникающей только в V сечении. Действительно, выражение изгибающего момента в IV сечении имеет следующий вид М(х)-МО -}-Qox4-Л1(х-г)° -} — р(х-б) 4- (10.77)) полезно запомнить Формулы J (x-a), (x—B), (x—C) и так далее…. (x—/) может быть положительным.
Если получится (х-это означает, что соответствующая нагрузка Людмила Фирмаль
расположена на правой стороне рассматриваемого участка Н). Изгибающий момент 7I0 и боковая сила Qo, действующая на участок, совпадающий с началом координат, называются статическими начальными параметрами. Составим дифференциальное уравнение упругих линий на участке V:= — Sch[m0++M(x — #+P (x -«) + + —— ( | 0 −7 8 ) Он объединяет обе части равенства, не открывая 283 скобки. Тогда мы получаем — L g-EIJ X» Интегрируйте снова, мы находим w () = — например 4 — +Q°4 — +M+ (х-CP_(х-ДП (х-с)*, (х-Д) * 7? С 24 по 120-120 2«Р+С у Дж. (10.79) п(*-«)’ , 6′ 4 * сухой 4» • (10.80)) Дифференциальное уравнение упругой линии IV сечения записывается следующим образом: d2w (х) _1 — dx2^ » Е7 /Mo4-адррес qox+м (х-а)°+р(х-б)+ Если вы интегрируете его дважды、 +Qо + * — ^ + Л1 £=£+ 4-Sivx4-Д/ви. 4 Ясс (10.81)) Один. dx EJ +Р — ^-+Я^^ МО~+Д o~^+л ЯП с — > — с)4j_b{К~С? Двадцать четыре 4-120 Теперь мы можем показать, что соблюдение правил и Интеграла уравнений упругой линии гарантирует равенство
любых констант в IV и V сечениях. Фактически, если поставить формулы (10.79) и (10.82) x-d из условий гладкого сопряжения графика, то получится 6 (d)/v- — — gj , (д-с) 3 4-КК — ©(>■) = ДГ м Шесть. Х3 4~м(х-а)4 ~ 4 ~ ф/г]; (10.82) п (*- з Шесть. + (10.83) Компилировать [ти^4-Qo4«+м (д-А) 4- 6г 24 + * L.±= * 34^±.+ После.| Следовательно, S/g=su. 4-Сив] = ©(г) в= Яаа+ (10.84) 284Ci=и= Если положить X=d в уравнения (10.80) и (10.83), то из условия непрерывного сопряжения графика w (d) w==w (d) v, Djy=*Dy. S/n= * Civ W Cv= «f(10.85) Dj = Du = Dju=» Div=Dv=(10.86) получаем уравнение первого сечения с учетом угла поворота и уравнения прогиба в первом сечении и членов, учитывающих постоянную нагрузки, приложенную к пересечению этих двух интегральных геометрических уравнений (10.79) и (10.80).: +(?Подставляя 0-g-x-0 в эти уравнения, b (0)=e0=CIEJ -, w(0)=Yu-DIEJ.
Поэтому произвольные константы C и D равны при каждом угле поворота и отклонении в начале координат. Начальными параметрами являются углы поворота отклонения w0 и 0. Подставляя значения C и D в уравнение (10.80), получаем общую формулу для отклонения любого сечения балки: w (x)=w0+0O% +L IG TR2 (X~L n (X~f L_v)).)__ Шесть. [(]С 24 24 б R (x-4) 6 Сто двадцать. дуплексный W W= — £7 L10x+Qо » 2-Б|»х>СХ -} — Д Дж. Х2 1, (10.87)) (10.88) (10.89)) (10.90) Подходит для- (10.91) Для некоторых моментов и сил, а также некоторых участков распределения нагрузки уравнение записывается в виде; Уравнение(10.92)обычно называют универсальным уравнением упругих линий. Следует отметить, что это уравнение применимо и к расчетной схеме балки. Дифференцируя уравнение(10.92), получим уравнение угла поворота сечения: 0 (х)=0о-Джей (10.93) В формулах (10.92) и (10.93)
мы подставляем только»нагрузку», расположенную на левой стороне рассматриваемого участка. Знак Терма определяется знаком соответствующего коэффициента мощности. Таким образом, определение смещения методом начальных параметров сводится в основном к определению значений начальных параметров Qo, Mo,©0, w0. Статические начальные параметры QN и Mo получены из условий равновесия пучка. Геометрические начальные параметры 0O и w0 определяются из условий опоры. Уравнения (10.92) и (10.93), полученные для любого сегмента пучка, подходят для всего пучка. Как правило, выбирают начало координат в точке левого края балки. Рассмотрим пример определения смещения балки методом начальных параметров. Консоль оснащена равномерно распределенной нагрузкой в половину длины (рис. 281, а) для определения прогиба балочного сечения. Оси x К=А и Х=2А Ки.
Напишите уравнение на упругой линии для правого участка балки. Так как распределительная нагрузка ломается в точке С, то при введении компенсирующей нагрузки той же силы ее следует продлить до края балки(рис. 281, б). Уравнение упругой линии обычно U/(Х)=^О+Е вол+~Г7[М0-2Г+ » 5г=2C, то получится формула для прогиба свободного конца консоли: Если поставить формулу (10.97) x==a, то получим формулу отклонения в точке C: рис. Двести восемьдесят два (, Около 8 ) Может быть. 282 определяет отклонение и угол поворота в точках C и D. Запишем уравнение упругости^l^NII в крайнем правом сечении балки^BD, где Iw(x)=L-2)++d{x4/°J-(10.99) считаем, что начальный параметр уже известен и записываем (10.99). также возможно: Со= — = — — — г-КЖ; девиз. Для определения геометрических начальных параметров существует опорное условие: x-0w (0)=wA=0, x==/w (G)-wB=0. Из первого условия ссылки это выглядит следующим образом tiy0 = УА = о. 287-е опорное условие является №. (/)=@о / 4 —
Откуда О= , Один. Т-Р (-4) 4 EJ8I1 6h24 y _57ql * ° «»384EJ’ Теперь уравнение упругой линии сечения балки BD имеет вид 57qP, 7х» 384 x 8q3 ‘+ — Y— » 3! ——— 4 4! 4! (10.100) в Чтобы найти движение точки D, достаточно поставить такую Пять. Уравнение x~I, то / 5D[57 5 7I(5\3,11 I(1\3. .. 167G_N л E G~ ——[536″ ~например~ ~ 11 ~ EG’ Один. ~^Г То есть Компания WD= — 0.11-г -. (10.101) Чтобы вычислить смещение точки С, нужно написать уравнение упругой линии в области, где находится эта точка. Поскольку он находится в разделах gr и C e/I//, мы пишем уравнения упругой линии первого раздела. Для этого из уравнения (10.100)необходимо придумать член, соответствующий нагрузке, которая появляется только на II и III участках. То есть в уравнение должен входить только один коэффициент силы — Ра — Таким
образом, уравнение упругой линии первого сечения принимает вид <10-102) Если мы поставим x » =4-то получим уравнение отклонения точки C: 0, 0 5 6^ -. Для вычисления угла поворота любого участка балки 288 необходимо выражение, описывающее угол поворота соответствующего участка балки. Уравнивание угла поворота для сечения БД получается дифференцированием уравнивания(10.100): (x-0 8 (10.103) Пять. Если мы поставим здесь x= -/, то получим уравнение угла поворота сечения D: — 4 (4)3+4- (Т)3]> — Г — — Следовательно. 0O= — 0,56-g (10.104)формула для угла поворота первой секции (секции AC) получается путем дифференцирования уравнения(10.102): «=- Я — [^- ‘Р-С -Т»] — < / 0105> Итак, если x= — y, то получим формулу угла поворота сечения C: ■ ) qp15EJ~384 qP EJ Семь. 8 • 2 • 22 Расчет жесткости на изгиб. Освоив методику определения прогиба и угла поворота,
можно проверить не только выбор размеров поперечного сечения балок из условий жесткости, но и жесткость балок. По абсолютному значению максимального отклонения балки на F, а также по допустимому отклонению на [ / ], обозначенному стрелкой, получаем условие жесткости балки: / < [ / ! •(10.106) Допустимые значения отклонения устанавливаются на основании экспериментальных и эксплуатационных данных. 43, например. Для балок, нагруженных на расстоянии а-4М от левой опоры, к моменту централизации / I= = 12ТС■м(рис. 283), поперечную силу, изгибающий момент, строят фигуру угла поворота и прогиба сечения, а также подбирают поперечное сечение двутавровой балки из условий прочности и жесткости; [о]=1600кгф/СМГ; [/]=/; 10В-2770 Теперь, когда мы определили опорную реакцию 289, мы построим график боковы
х сил и моментов. Перемещение характерного участка определяется в соответствии с порядком приведенного выше рекомендуемого решения. Запишем уравнение прогиба участка SV: Вт(х)=ц0-я-6 0х ч (10.107) Так как начало координат выровнено с левой опорой L, y0=и>l=0. По второму критерию w (/) =wB=0. iv Вот ты ешь Двести восемьдесят три Из уравнения (10.107) PRN1=6m получаем e. 6 (/ — 4)*] = 0. (+ 4 — [4 Откуда во=(10.108)ЭЖ * Подставляя формулу (10.108) в Формулу (10.107), запишем уравнение упругой линии Уча — (м) ТСН стке СВ в ее окончательном виде:| — 8х+ ——6 (x-4) J•(0.109)) «М» 4 Уравнения упругой линии на участке L C записываются следующим образом: е — (- «+4-)- И — [-4<М-Ч Дифференцируя уравнение(10.109), получим уравнение угла поворота балочной части.: Вт(х) —. (10.110) в Восемь. Один. b (x)= — ^ — [-8+x2-12 (x-4) J.(10.111)чтобы построить
график 6, необходимо вычислить угол поворота на границе этого участка: −84-4*8 ЭДЖ; b = b (6)= — A- [ — 8 + 6»- 1 2 ( 6 — 4 ) ] ^ — а -. Если Е измеряется в кгс / см2, а в см, чтобы получить угол поворота J-4 в радианах, нужно умножить правую часть на 107. Затем л 8 * 107 около 4. 107e ы= — Е7—Рю ЭВ= — гы-рад. Дифференцируя уравнение(10.110), получим уравнение угла поворота сечения L: Один. 8 (х)=—8×2). (10.112) Угол поворота в границах этого участка уже известен. Таким образом, можно построить график G1. В 1 участке 0 и w полученные координаты после окончательного расчета откладываются.
Дж==7780cm4. Двести девяносто один Для границ участка отложите вертикальную ось 8•107_8•107 с l=e 0= ——— & ——rad и 9S= — RSD. Вершины этих вертикальных осей согласно уравнению (10.112) соединены параболической кривой. Q>0, поэтому парабола 0 должна быть направлена вниз выпуклой частью (стр. 5p. см. 280). В точке А касательная линия графика должна быть параллельна оси абсцисс (см. пункт 1). Точно так же мы занимаемся строительством на месте ул. Чтобы построить график отклонения, вычислите максимальное отклонение. Это делается в разделе 0 (x)=0. Запишите это условие: 0 (Xf)=8+ / 2)=0, Откуда х/=2.83 м. В этот момент
отклонение I имеет экстремальное значение C==/. Рассчитаем величину прогиба стрелы, подставив формулу (10.110) x=xf. 2.83 3. (21-2. 83*) м= — Эдж 0.943 * 16 м Измеряются ли E и J в кгс / см? Каждый и см4. Поэтому, чтобы получить сантиметровый прогиб, нужно умножить правую часть на 10E: 15.09 ЭДЖ 109 сантиметров Чтобы построить график отклонения, необходимо также вычислить отклонение в точке C, которая является точкой перегиба графика отклонения(в этом отношении знак задается как уравнение изменения (10.110) x = 4m в момент графика: У(4)= 4(24-42*) 32 3£7-3M’ Или 10.6 ЭДЖ 109 сантиметров Мы откладываем вычисленную ординату от базовой линии. Согласно уравнениям (10.109) и(10.110), график отклонения должен быть очерчен кубической параболой в обоих сечениях. На сайте АС момент М>0, парабола вогнутая здесь, так на сайте СВ момент Л4<0, парабола вогнутая(стр. 4). Перейдем от условия жесткости к выбору поперечного сечения балки. Состояние жесткости<10.106) принимает вид 15.09 ЭДЖ Ю9 и M<[/Б
Откуда J>p L t g109cm4-E=2 * 105 кгс / см? И разрешенные стрелки[/]=I Шесть сотен. Нам нужно 1 см Момент инерции От 15.09•10* 1-2-10Э см4=7545cm4. По каталогу ассортимента 10(Приложение 1)видно, что нужной двутавровой балки нет. ZOA, его Момент инерции J=7780cm4. Необходимо проверить интенсивность выбранного двутаврового пучка Ns ZOA, момент его сопротивления равен UZ=518 см3. Вычислите максимальное напряжение:^до 800 000s l9r «» o°max — C/ — = — gig — — — =145kgf / cm2<[o]=1600kgf / cm2. В результате обеспечивается прочность балки. Расчет средней навесной балки. Универсальное уравнение и угол поворота упругой линии, полученные здесь, получены из рассмотрения поперечного сечения CL. 280, Б), который не имеет промежуточного шарнира на балке и нарушает гладкость изогнутой оси. Поэтому, принимая во внимание всю балку и оставляя
общее начало координат для всех сечений, необходимо учитывать эти различия при непосредственном определении смещения поперечного сечения SF балки, расположенной справа от шарнира S. Однако можно показать, как обобщаются уравнения метода начальных параметров в случае балок с промежуточными шарнирами(рис. 280). Для этого мы пишем дифференциальные уравнения для секций BS и SF и интегрируем их дважды: для секций BS (РЗ (х)7и (х). Jx2~~EJ’ Вт (х) с — J ДХ J в — ’ХР дх+с» х+Д»; Для этапа СФ (Пуд (х))) dx2 ″ EJ9 Вт(х)=ф ДХ ф л^-D х+с » военторга+ОНП.
(10.113) (10.114) (10.115) (10.116) Из-за наличия шарниров левый и правый углы поворота точки S будут различаться в зависимости от угла A. (S)»=W(s)np;©(s)j,+a=©(s)np. (10.117)) (10.118) Заменить равенство (10.117)и (10.118)соответствующими значениями из выражений(10.114), (10.116) и (10.113), w (s) и 0 (s), 292(10.115), при x=s, найти Opr=—as+Dn из»—|-A-SPR » Sl5 4-PL=CnpS4 — Opr-равенство(10.119) и(10.120). (10.119)) (10.120) (10.121) Подставляя уравнения (10.119) и (10.121) в уравнения (10.115) и (10.116), можно записать уравнения вращения и прогиба в СФ-сечении такого вида:
0 (x)=j — ^7-dx4 — SL4 — (10.123) так как было обнаружено, что любая константа C и D слева от ее шарнира S все одинаковы, соответственно, в ней представлен угол поворота и прогиба, но от шарнира при наличии вопрос ЛП.. библиотека FFTW и И £GRG Я Рис двести восемьдесят четыре Гаше п Один. 2б Дж’mouthed Я (с Рисунок 285 Слева от рассматриваемого раздела формула для этого раздела (10.92) принимает следующий вид ++а(х-с)+тг»+® >
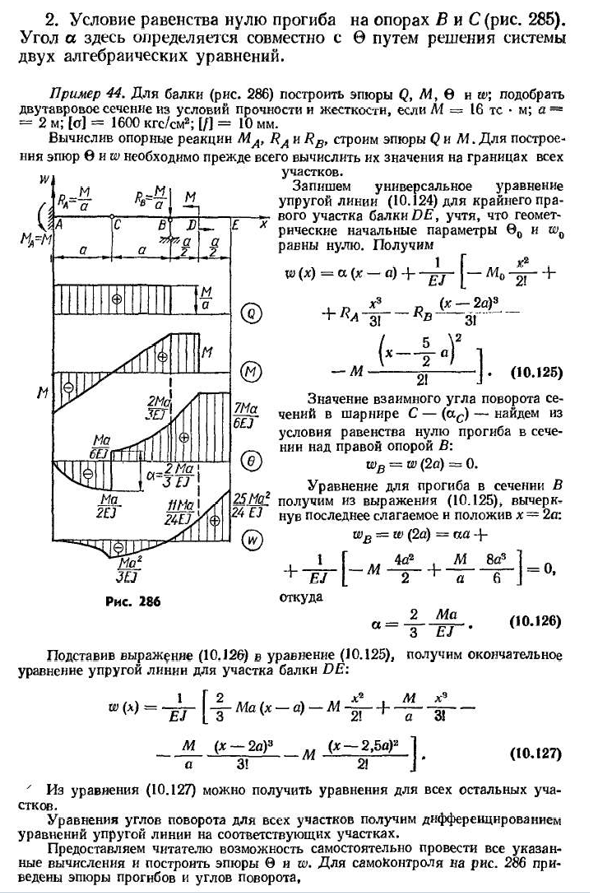
т г+ +Ц0 > 24) Угол поперечного наклона a является дополнительной неизвестной величиной в универсальных уравнениях w (x) и 0(x). Как и в случае с начальными параметрами sh0 и 0O, он определяется из исходных условий. В зависимости от типа расчетной схемы балки существует два основных варианта дополнительных опорных условий:1. Состояние нулевого прогиба правой опоры (рис. 284). Поэтому определяется только угол а. 2932 поддерживают состояние равенства нулю отклонений B и C (рис. 285). ОС определяется с помощью O путем решения двух алгебраических уравнений. Пример 44. D-лабораторная балка(рис. 286) построить участки Q, M, 6 и w; M-16TCm; a= — 2m; [o]=1600kgf/cm2; [/] — для 10 мм, подобрать I
сечение по условиям прочности и жесткости. После вычисления реакции поддержки MA и RB, постройте график Q и M, чтобы построить график b и o? Сначала нужно рассчитать значения на всех границах Двести восемьдесят шесть Сайт. Напишите универсальное уравнение упругой линии(10.124) для большей правой части балки, учитывая, что начальный геометрический параметр равен 0O и равен нулю. Получаем w (x)=a (x-o)N +^л Я не уверен. (10.125) Значение взаимного угла поворота сечения в шарнире C — (AC) — находим из условия, равного нулю прогиба сечения на правой опоре: wB~w(2A)=0. Уравнение для прогиба сечения B получается
из Формулы (10.125), которая пересекает последний член и ставит x=2A: — w(2A)=PA+G La 4a2, M8a3 — ——- — +4 Откуда = 0, (10.126) + Подставляя уравнение ’2MA a-3EJ’ (10.126) в уравнение (10.125), получаем конечное уравнение упругой линии относительно поперечного сечения балки DE: G2, x * l*, M X9 + —- — М(Н-2А)3LL(ч-2,5 а)2 1а3! 2! Из уравнения (10.127) можно получить уравнение J’всех остальных графиков. Уравнение угла поворота всех секций получается путем дифференцирования уравнений упругих линий соответствующих секций. Мы дадим читателю возможность самостоятельно выполнить все эти расчеты и построить графики 0 и W. 286 приведены графики углов отклонения и поворота. (10.127) 294перейдем до выбранного поперечного сечения балки.
Максимальный изгибающий момент мм AKS== / VI=16TSm. условие прочности от\wV7 \ > ^max1, 000a=— 1 6 0 0 — =в диапазоне 1000 м ’ принимаем двутавровое число 45, для которого W=1231cm8; J=27 696cm4. Давайте проверим, выполняется ли условие жесткости. Найти количество прогибов стрелы:.. 25МА 25 16 • 2* я не уверен. 10Y I W e * 24EJ~24’2′ ■10E ■ 27 696CM ’2 0CM’ жесткие условия (10.106) не соблюдены: f=1.20 cm>[/]=1cm. Поэтому, исходя из условий жесткости, размеры поперечного сечения балок должны быть увеличены: ф 25 1 6 — 4 я не уверен. 10-й ф 24 * 2 • 106 J z и » 1 см<из Формулы (10.128) 95 16 * 4 * 10E Jz> «24——- 2 ■ 1B» f cm * ^33 4 0 0 0 см<* По ассортименту у меня луча нет. Примите 50(J=39 727cm4).
Смотрите также:
| Основные понятия о предельном состоянии | Напряжения и деформации при растяжении и сжатии. расчет на прочность и жесткость |
| Расчеты при растяжении и сжатии | Расчеты при кручении |

