Оглавление:


Определение перемещений в балках переменной жесткости
- Определение смещения балки Переменная жесткость Прямое интегрирование уравнений упругих линий переменных жестких балок возможно только в частных случаях, когда N-M-x-F (X) может быть записано как интегрируемая функция. Примером такого случая
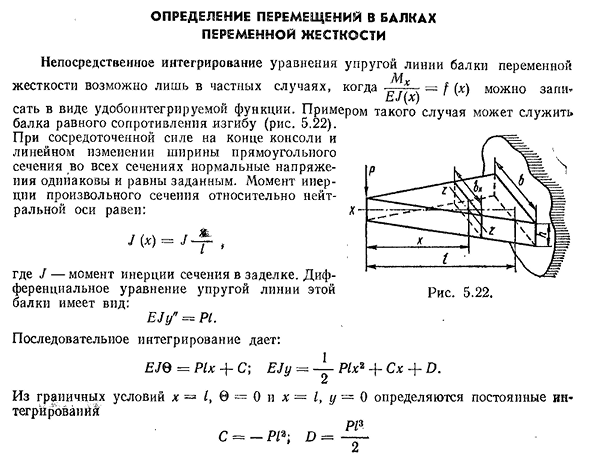
может служить балка с равным сопротивлением изгибу(рис. 5.22). Благодаря линейному изменению силы, сосредоточенной на конце консоли и ширине прямоугольного сечения всех секций,
нормальное напряжение является одинаковым и равно заданному напряжению. Людмила Фирмаль
Момент инерции любого сечения относительно нейтральной оси、: /(З)=/Л — , Где J-момент инерции участка в уплотнении. Дифференциальное уравнение упругой линии этой балки имеет вид Ely » = Pl. Последовательное интегрирование выглядит следующим образом: EJQ=P1×4-C; EJy= — 1-Plx2+Cx+D. Интегральная константа определяется из граничных условий#1, 0=0 и x=I, y=0 П13 С—П12;Д=-
Уравнение отклонения 117i имеет вид: EJy=~P1x^ — PPx1 — СТР Два. Например, максимальный прогиб (конец консоли) будет равен: PP Умкс-2.’ Метод начальных параметров балки переменного поперечного сечения Xia seonie, которая изменяется поэтапно для определения угла отклонения и поворота балки, заменяется балкой
- постоянной жесткости и эквивалентной.= ———— коэффициент актерского мастерства. Поэтому все по-Е’й н, нагрузка будет меняться во времени. Цели планирования: 1) определить модуль отливки для каждого участка балки;2) определить модуль сечения усиленной опоры АР, работающей в пределах каждого участка балки. Например. Составьте уравнение для упругой линии балки. Как использовать
5.23, a. Коэффициент жесткости шаговой балки: Vj: EJ2: EJ3=1: 2: 3. Решение. Когда жесткость эквивалентной балки равна жесткости промежуточной части EJ3=EJ2, вычисляется коэффициент уменьшения: EJa_ _ EJ2_2 _ EJ2! 3_3′ Умножьте все силы на соответствующий коэффициент: Два. А2=2Р; А2Р=Р; a3p все= —
П. Создайте предварительный чертеж изгибающего момента и боковых сил для этого(рис. 5.23, б,&): DL71=(А2-ОЖ)2ra= — 2ra;2 Дм3=(А3-А2)2ra Людмила Фирмаль
— — — РА;3 Р Р Р Р Р Aq1 по=(«2-МЮ) -= —— AQ2 — (3)— п ~ми’~ Построим эквивалентный пучок (рис. 5.23, г) для обычных балок его упругие ЛП NIIの式を書く:EJy=E/u0-f-EJ@ax + Zrx3 6 2Р (х-а)3 2ra(х-2А) Р(х-2А)3 2 12 Р (х-з)3-6 R (X-4A) 3 36 2Р(Н-5а)3 18 Шесть. Это отклонение видно при вычислении начального параметра. Специфика, определяющая перемещение балки переменного сечения, заключается в преобразовании фиктивной нагрузки. Умножьте этот коэффициент на 118 _E ДЖ И n-EJn ’, где EJ-жесткость некоторой первой секции; EJn-
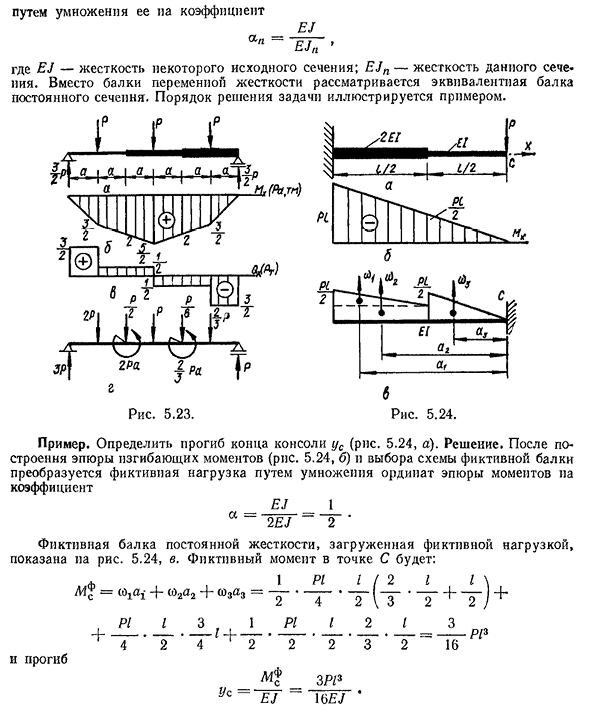
жесткость данной секции. Вместо балок переменной жесткости рассматривается эквивалентная балка постоянного сечения. Порядок решения задачи иллюстрируется примером. Рис, 5.23. Например. Определить прогиб конца консоли(рис. 5.24, а). Решение. После построения графика изгибающего момента (рис. 5.24, Б) и выбор
метода фиктивной балки фиктивная нагрузка преобразуется путем умножения вертикальной оси момента на график коэффициента ia EJ1 на рисунке показана балка ~ 2′ ~ 2’dummy постоянной жесткости. 5.24, V. фиктивный момент точки C равен*, 1Pl I(2I I\L4 ′ = — f w2a2+co3a3= — —— ——- ————— + — J+Pl I3;, 1Pl I2I3+ 1 2 4 ~2 2 2 3 2~ = l b~R / 3 И отклонение. _313 U C~EJ~16EJ’
Смотрите также:
| Графический способ построения упругой линии | Статически неопределимые балки |
| Влияние поперечных сил на прогибы | Миогопролетные неразрезные статически неопределимые балки |

