Оглавление:


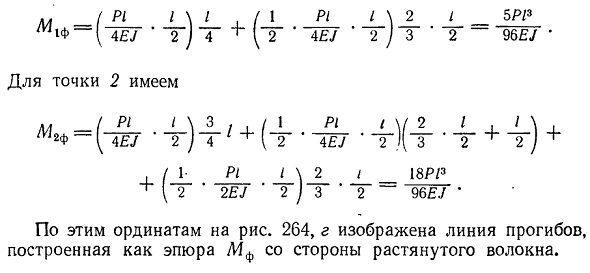

Определение перемещений в балках переменного сечения
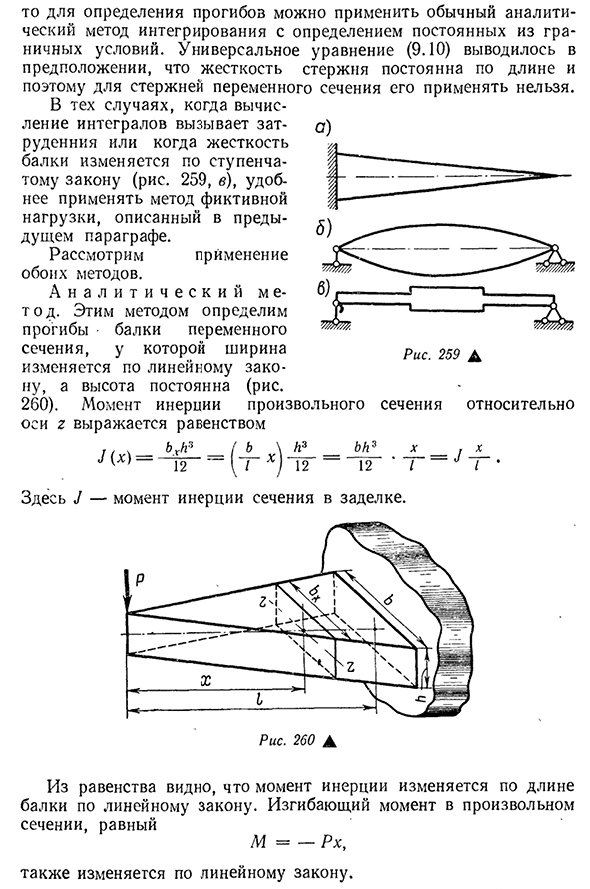
- Определение смещения балки Переменное сечение Если жесткость балки изменяется по длине по какому-либо закону(рис. 259, А, Б, С) Е] (Х)=/(Х) И когда мы интегрируем дифференциальные уравнения изгиба (Около 1 s (H2~E и h) (U. 1B Могут возникнуть трудности. Если правая часть дифференциального уравнения (9.13), где и числитель, и знаменатель являются функциями x, может быть представлена как легко интегрируемая функция М Е. 1(ч.) = = Р(Х), 298 стр. 259А Для
определения прогиба может быть применен обычный аналитический метод интегрирования с определением констант из граничных условий. Универсальное уравнение(9.10) было выведено в предположении, что жесткость стержня имеет определенную длину, поэтому его нельзя применять к стержням переменного сечения.
Если расчет интеграла вызывает ЗАТ-рудение, или жесткость балки Людмила Фирмаль
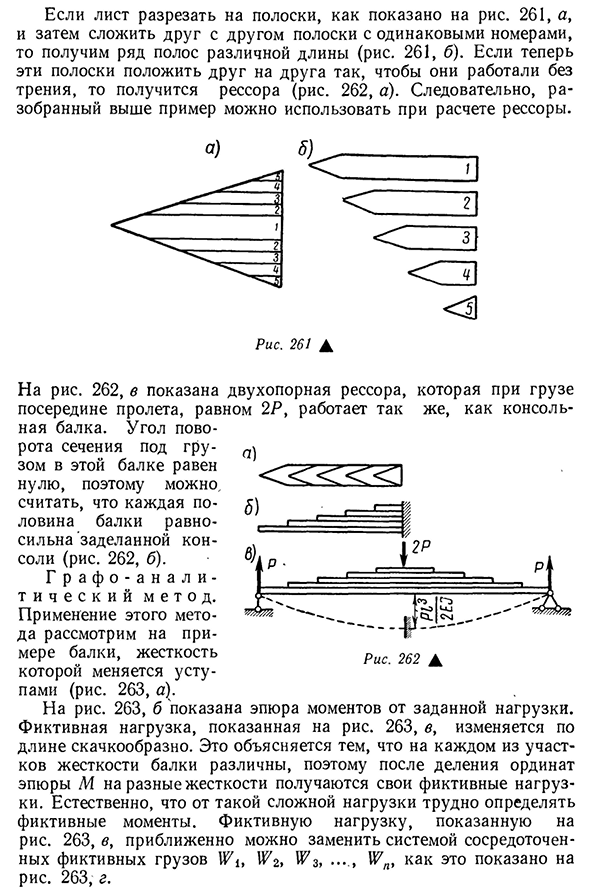
изменяется по ступенчатому закону(рис. 259, с) удобнее применять метод фиктивной нагрузки, описанный в предыдущем пункте. Рассмотрим применение обоих методов. Это позволяет повысить производительность вашего приложения. Этим методом определяется прогиб балки переменного сечения, ширина которой изменяется по линейному закону и постоянна по высоте. 260). Момент инерции любого сечения для оси g представлен уравнением •/(х)=^2-=
(т-х)-ТГ=-[2 —• Здесь находится Момент инерции участка в уплотнении. Рис 260Л Из уравнений видно, что момент инерции изменяется по длине балки по линейному закону. Изгибающий момент в любом поперечном сечении, равный M= — Px, который также изменяется с законом линейности. Если ось 299y направлена вниз, дифференциальное уравнение для линии отклонения принимает вид М г x2E< / (х) ( — ^ ) Икс Иезекииль. — Поскольку правая часть дифференциального уравнения постоянна, интегрирование
- становится простой задачей. Последовательно интегрируясь, мы получаем (ВНУТРИВЕННЫЙ s1x=Ф= — Р1. п Е7 — х+с; О=tg4 — +СХ+о — <б> Граничные условия следующие: < Р = 0; V=0. Получено из первого условия уравнения (a): Р-Р Ми^ +С=0; Р-Р Е } Из второго условия по формуле (b) получаем: РУБЛЕЙ ^2Е Е } / +Я=0; Б-Р1~ №.’ Подставляя значение найденной константы b (b), получаем уравнение отклонения оси пучка ____R1x2R RХ. ПП В~2Е^Е/+2Е/’ Если вы поставите X=0, вы найдете максимальное отклонение в конце консоли Ви тах = ПП 2Е/2Е’ Как показано в §69, эта балка является
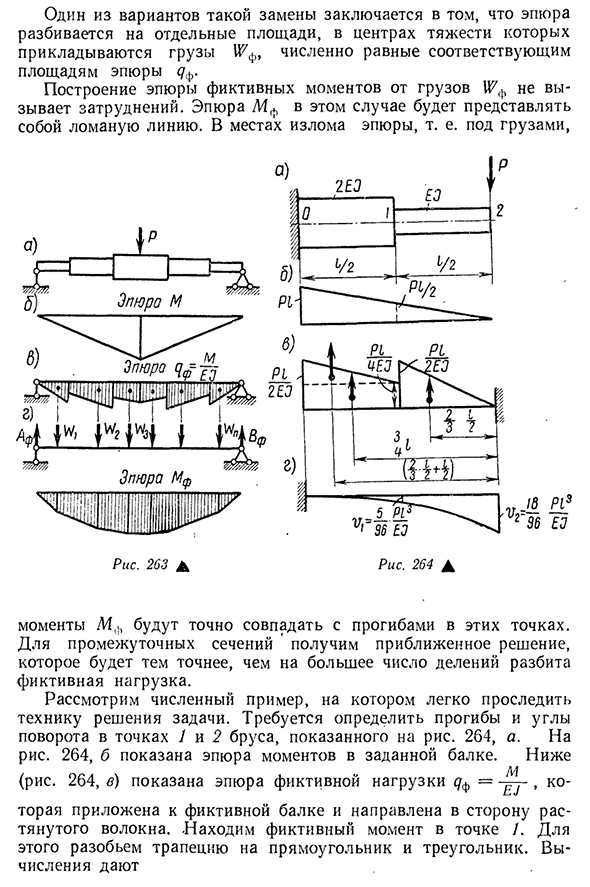
балкой с равным сопротивлением изгибу. Как балка постоянного сечения, имеющая одинаковую прочность в уплотнении, она имеет в полтора раза больший прогиб. Такая система выгодна для пружин, которые обладают достаточной прочностью и в то же время должны обладать большой гибкостью. Например, обычная автомобильная пружина имеет тот же закон изменения жесткости, что и рассматриваемая балка. Если лист разрезать на полосы, как показано на рисунке. 261, а, затем сложим вместе полоски с одинаковым числом, получим ряд полос разной длины(рис. 261, б).
Когда эти полоски надеваются друг на друга и начинают работать без трения, Людмила Фирмаль
мы получаем пружину(рис. 262, а). Итак, приведенный выше пример можно использовать для расчета пружины. Но) Для риса. 262, b, работает так же, как консольная балка, с нагрузкой в середине пролета, равной 2p, показывая две опорные пружины. Поскольку угол поворота секции под нагрузкой этой балки равен нулю, каждая половина балки является «закрытой консолью» (рис. 262, б). Г Р А Ф О-а н а л и-Т И Ч Е С К И Й м е т о д. Применение этого способа рассмотрено на примере балок, жесткость которых изменяется в зависимости от полки (рис. 263, а). Для риса. 263, b показывает график моментов от заданной нагрузки. Как использовать 263, b, изменения
по длине прыжков и границ. Это связано с тем, что в каждом сечении балки жесткость разная, поэтому после деления вертикальной оси участка М на разные жесткости, их мнимая нагрузка естественно от такой сложной нагрузки, трудно определить мнимый момент. Как использовать 263, это приблизительная сфокусированная псевдонагрузка 1^1, G2, 1G3, может быть заменена системой… Как использовать 263g Необязательным условием для такой замены является то, что участок делится на отдельные области, и применяется нагрузка 1gf, где центроид численно равен соответствующей области участка DF. Построение фиктивных моментов от нагрузки 1gf не вызывает трудностей. Сюжет МФ в это
м случае будет представлять собой пунктирную линию. Место излома участка, то есть под нагрузкой, Момент MF точно совпадает с отклонением этих точек. В среднем разделе мы получаем приближенное решение, где чем больше делений делится фиктивная нагрузка, тем она точнее. Легко проследить технику решения задачи, рассмотреть численные примеры. Необходимо определить прогиб и угол поворота точек 1 и 2 стержней, как показано на рисунке. 264, И. Как использовать 264, б показан сюжет какой-то момент луч.
Ниже(Рис. 264, с) показывает график фиктивной нагрузки 7F=, которая приложена к фиктивному лучу и направлена на растянутое волокно. Найдите фиктивный момент в точке 1. Для этого разделите трапецию на прямоугольники и треугольники. Расчет дает 302I\2 / Два. 5П/3 96Э/ * Для Пункта 2、 . /1-P1I\2 / _18P / 3 +\2 2 2/ \ ‘ 2)3 2~96Э.1’ Эти координаты на рисунке. 264, g показывает линию отклонения, построенную как график MF на стороне растянутого волокна.
Смотрите также:

