Оглавление:





Определение перемещений способом фиктивной нагрузки (графо-аналитический метод)
- Определение перемещения методом Фиктивная нагрузка(анализ графика Метод) Из теории изгиба (см.§64) мы знаем дифференциальную зависимость, заданную уравнением (8.3), связывающим изгибающий момент с нагрузкой, 4A2M AH2~d’ Сравним это уравнение с дифференциальным уравнением для оси криволинейной балки А2®м~~ЭГ * Поскольку существует полная аналогия между этими двумя уравнениями, проблема определения отклонения состоит в том, что оно принимает момент от некоторой условной (гипотетической) нагрузки в фиктивной балке. М е.Один • При определенных условиях этот фиктивный момент нагрузки равен отклонению V на заданной балке от заданной
нагрузки, возникающей в результате A4F. И я думаю, что И 293 можно сделать вывод, что угол поворота в данной балке численно равен мнимой боковой силе в мнимой балке. Равенство V = MF, F C?Ф Аналогия с граничными условиями Отчет) // %И = 0 ф=0 Пять.) СЧ=0 0С~о Рис 255А 17-0. (П * 0 Слева, но не выше. СЧ* * о Другими словами, график углов отклонения и поворота в данной балке должен наблюдаться во всех точках двух балок полностью и для того, чтобы удовлетворить это требование величины, необходимо иметь
полный набор из двух балок. В качестве примера рассмотрим балку, запечатанную с одного конца. 255, а). На левом конце этой балки Людмила Фирмаль
отклонение и угол поворота равны нулю, а на правом-он отличается от нуля. В крайнем левом фиктивном луче MF и FF должны быть равны нулю, а в правом-отличаться от нуля. Этим требованиям отвечает балка с уплотнением по правому краю(рис. 255, б). Данная балка является фиктивной балкой, в которой должны быть определены угол отклонения и поворота, определены мнимые моменты и мнимые боковые силы. Каждый луч-это манекен. За столом. Приведены 9 различных случаев фиксации данного пучка и
соответствующего фиктивного пучка. Фиксация антенной балки выбирается при условии, что существует совершенное соответствие между C и CP в данной балке и MF и антенной балкой на конце балки и опоре. Интересно отметить, что данный Луч и фиктивный луч взаимозаменяемы. 9, после этого каждый фиктивный Луч будет одним, Котор дали к левой половине таблицы. Остается уточнить вопрос о правилах знаков. Показано, что при построении графика момента реального пучка и мнимого светового пучка со стороны проволочного волочильного волокна, а накладная нагрузка направлена от оси пучка в сторону волочильного волокна, линия отклонения в данном пучке автоматически совпадает с графиком мнимого
момента в мнимом пучке. 294T ABL и C a9 Балка фиктивная балка Но В Но В На G ‘#77^7’ М^О нет. y В В \ Эй, 0. Ф О Ф О Ф О Ф О С а в С А Б а _ п Но * 0, l u * 0 ФО Хо Один Ф О Ф О Ф О — И так далее и тому подобное Около 4 GF около 5?^Чго с,=0fo<Ф О Ф О Условимся, что вращение касательной к оси данного пучка считается П О Л О Ф и т е л ь н ы м. тогда знак u SR I@f A в Т О М И Ч Е С К и й в п А Д у Т. Рассмотрим некоторые примеры применения метода фиктивной нагрузки. П р и М Е Р1. Определите прогиб конца нагруженной консоли силой Р(рис. 256, а). Сюжет момента показан на рисунке. 256, б. Так как мы разделили все продольные оси этого участка на жесткие е<7 и приняли его за мнимую нагрузку, то поместили это на фиктивную балку(рис. 256, в).
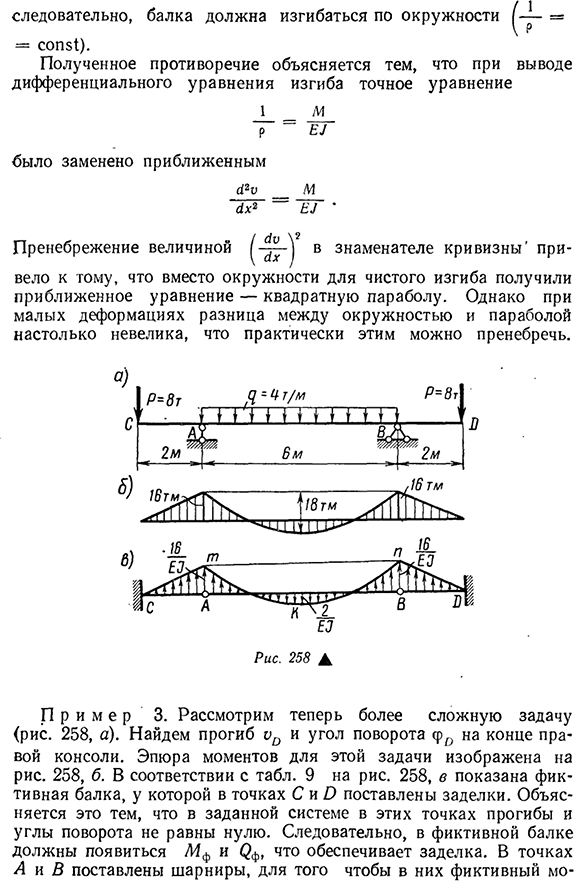
Фиктивный луч выбирается в соответствии с таблицей. 9. Печать фиктивной балки уже находится на правом краю. Согласно принятым правилам, мы направляем фиктивную нагрузку на растянутые волокна в данном пучке. Двести девяносто пять XB фиктивный луч (см. рис. 256, в) растянутое волокно находится внизу, поэтому продольную ось участка мнимого момента нужно уложить так, чтобы данный пучок изгибался. Участок L4f(Рис. 256, г) совпадает с эпюрой прогиба, которая обозначена пунктирными линиями рисунка. 256, а. Самый большой вымышленный момент (L4f) tah соответствует самому большому отклонению ut. Расчет дает П р и М Е Р2. Определите максимальное отклонение второй опорной балки, генерирующей чистый изгиб (фиг. 257, а).
Для риса. 257, b, C показывают график l4f и фиктивную нагрузку. Поскольку последние распределены равномерно, график l4f Людмила Фирмаль
очерчен на параболе квадрата с наибольшим моментом в середине пролета. Поэтому максимальное отклонение /Л Л Л Л Я не собираюсь говорить, что не собираюсь этого делать, но я это сделаю. В этом выпуске графики UIF и, следовательно, линии отклонения очерчены на квадратной параболе. Точно такой же результат получается и из аналитического решения. Однако на основе равенства (9.3) чистого изгиба балки постоянного напряжения 1м — =- Рот — = = сопло, p/’ 296 последовательно луч должен изгибаться в окружность= = SOP$1). Полученное противоречие объясняется тем, что при выводе
дифференциальных уравнений, точное уравнение загибается 1_m Р~Е} Он был заменен приближением 42o__М~нет ~ ~ ЭГ’ Игнорирование значения знаменателя кривизны привело к тому, что вместо круга для чистого изгиба была получена приближенная формула—парабола квадрата. Однако при небольших деформациях разница между окружностью и параболой очень мала, что можно практически игнорировать. $ / 5gm________ _ ,16 ТМ Е6 258а П р и М Е Р3. Теперь давайте подумаем о более сложных вопросах. 258, а). Найти прогиб и угол поворота СРО на краю консоли справа. Сюжет момента этой задачи показан на рисунке. 258b. согласно таблице. 9 на рис. На рис. 258, б показана
вымышленная балка, которая устанавливается для уплотнения с точками С и I. Это объясняется тем, что в данной системе в этих точках отклонение и угол поворота не равны нулю. Поэтому в нем должны появиться L7f и FF, которые обеспечивают уплотнение воображаемого луча. В точке расположены шарниры а и В, а в них воображаемый МО- 297) был равен нулю, потому что в данной системе отклонение этих точек равно нулю. Согласно правилам знака, фиктивная нагрузка направлена от оси балки в сторону растянутых волокон, поэтому она направлена в разные стороны на разных участках (см. рисунок). 258, в). Давление от центральной части балки до конца консоли легко определяется как половина общей площади участка фиктивной нагрузки, действующей на балку АВ. Эта область найдена как разница между двумя областями
прямоугольного Atpv и параболического крана (см. Рисунок). 258, в). И так оно и есть., ^(16-6-4 18-6)=Е1]2 * Теперь мы находим фиктивный момент в точке, равной отклонению/) (М ф)о, ОД-2+ Угол поворота определяется как мнимая боковая сила ‘ х 12. 1 16o_28(ЧФ) о-ФД е. 1+2 е.1 ‘ 2е.1’ При расчете размеры равны m, сила равна T, а в полученную формулу необходимо подставить жесткость,выраженную ТМ2, поэтому прогиб равен m, а угол поворота выражен радом.
Смотрите также:

