Оглавление:





Определение обобщенных функций. пространства D и D’
Определение обобщенных функций. пространства D и D’. Во-первых, мы определяем линейное линейное пространство функции O. для этого действительное число/? Подумайте о функции, определенной in. It принимает сложные значения. 59.3.Определение обобщенных функций. Пространство и О’ 521. Пространство, которое нас интересует, состоит из бесконечно дифференцируемых, компактно поддерживаемых функций (см.§ 55.2 для определения компактно поддерживаемых функций).При естественно определенных операциях сложения и умножения чисел все поддерживаемые функции образуют линейное пространство, а бесконечно дифференцируемые компактно поддерживаемые функции образуют свои подпространства. Это подпространство вводит понятие сходимости последовательностей.
Множество бесконечно дифференцируемых, компактно поддерживаемых функций представляет собой линейное пространство со сходимостью за счет введенной операции перехода к пределу. Людмила Фирмаль
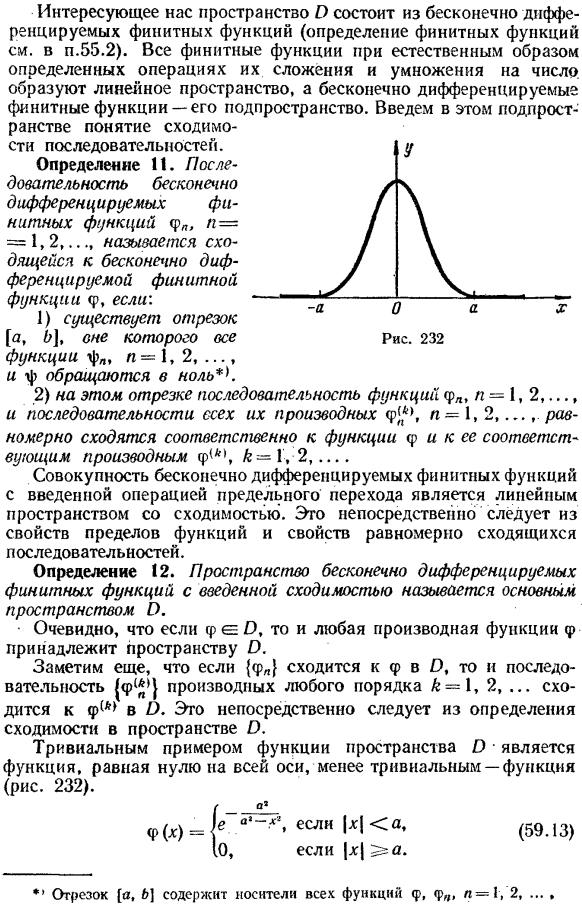
- Определение 11.Последовательность бесконечно дифференцируемых компактно поддерживаемых функций φ», η— один = 1,2,…, Называется сходимостью к бесконечно дифференцируемой компактно поддерживаемой P-if функции. 1) есть сегменты [a, b], внешняя сторона которого изображена на рис. 232 Функция φn, n-1,2,…、 И φ исчезает* ’ 1. 2) в этом отрезке последовательность функций φηn, η= 1, 2,…, И все их производные φ^, α= 1, 2,…Последовательность сходится равномерно к функции φ и соответствующей ей производной φ соответственно. (* \ k = 1, 2,…. It непосредственно следует из предельной характеристики функции и характеристики последовательности, которая сходится равномерно.
Определение 12.Пространство бесконечных дифференцируемых конечных функций с введенной сходимостью называется главным пространством b. Очевидно, что для φe 0 производная функции φ принадлежит пространству O. Также, если{φ»}сходится к φ при 0, то любая степень k-1, 2,…Производная последовательность разверните до φ (*в k).Это следует непосредственно из определения сходимости О. Тривиальным примером функции в пространстве O•является функция, равная нулю по оси, но менее важной функцией является функция (рис. 232). Рин!_ e если / x / a .0 если / lg / 5 = A. (59.13) F (х)= * В отрезках[a, b\, все функции φ, φ», η-1, 2,…17 Кудрявцев Л. Д. вып.2. поддержка включена. § 59.Обобщенная функция 522.
- Упражнение. 2.Докажите, что функция (59.13) бесконечно дифференцируема по числовой оси (см. (37.25)). 3.Докажите это для функции φО 4. Определение 13. Все линейные непрерывные функциональные функции, определенные в H, называются обобщенными функциями. Определение 14.Функция, определенная по всей действительной оси, называется локальной интегрируемой, если она может быть абсолютно интегрируемой на конечном интервале. Если /является локально интегрируемой функцией и является p, то произведение/φ полностью интегрируемо через axis. In факт, скажем,$ irr f s. [a, b] (см. раздел 55.2 для определения несущей функции f); функция φ явно ограничена. / φ(х) / ^ с、 ко х + сотрудничество, таким образом 4-Б 5 \ 1 (х)(р(х)\ х = ^ с (х) φ(х)\ топор ^ с ^ \ 1(х)\ топор.
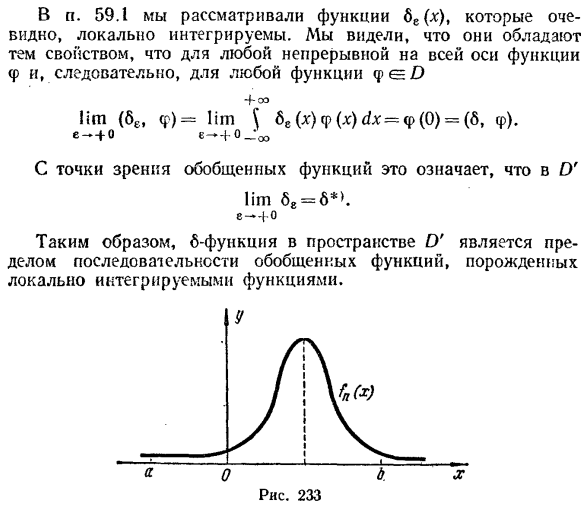
И Для локально интегрируемых функций / определить функцию ( / , φ) равен по уравнению 4-00 (/, φ)= 5 /(х) φ(х)ух. (59.14) КОМПАНИЯ. Эта функция является линейной и непрерывной. Своя линеарность obvious. It доказывает свою непрерывность. Пусть O нф = φ 71 ► сотрудничество Все η= 1, 2,…Например, отрезки[А, B], которые содержат zirrΦ» с. [А, B]и zirr Ф. [А, B] \поэтому 4-00 Я./(Φ) (/.Флорида), я ^ 5 я / (•*’11Ф (■ * ) ФЛ(х)\ ДХКОМПАНИЯ. Б, б. = 51 / ( * ) I / φ (x) Φα (x)| xx [φ (x) fl (x)\ Y \ 1 (x)\ xx-0 В [А, B] в в п + со. Таким образом, локально интегрируемая функция/(x) соответствует обобщенной функции ( / , φ)*.в этом смысле локально интегрируемая функция может рассматриваться как обобщенная функция. Константа, то есть обобщенная функция f, такая как ( / , φ)= +°° = c§(p (x) dx, где c-постоянная, Φ0 (особенно нулевая функция КОМПАНИЯ. l) порождается локально интегрируемой функцией f (x)= c. Кокс + 0°. * ’В этом случае обобщенная функция ( / , (p) порождается функцией/、 59.3.
Следовательно, функционал, равный константе, не принадлежит к рассматриваемому классу функционалов. Людмила Фирмаль
- Определение обобщенных функций. Пространство И И И ’ 523. Напомним, что линейный функционал всегда означает линейную однородность functional. So, функция /, равная одной и той же константе c на всех элементах линейного пространства X, является линейной функцией, но не однородной. Если ХууЯХ -, я и / R числовые, то / (x)= f(y)=/(х+ру) = C для указанной функции. Если она линейно однородна, то/(хχ+=) = / /(x)+ p /(y)= (++p) c. если + + ρ= 7 ^ 1 i(ХХ+)) φ / / (x)+ p / (Y), то функция / не является линейно однородной. Упражнение 4.Докажите, что 2 непрерывные функции на числовой оси различаются только в том случае, если генерируемые обобщенные функции различны. Иногда обобщенная функция является.
Смотрите также:
Решение задач по математическому анализу

