Определение нормальных напряжений при внецентренном растяжении (сжатии).
Вначале рассмотрим диск, к которому приложена сила F в точке А (рис. 118). Переместим силу F тaк, чтобы ее точка приложения оказалась в точке В.
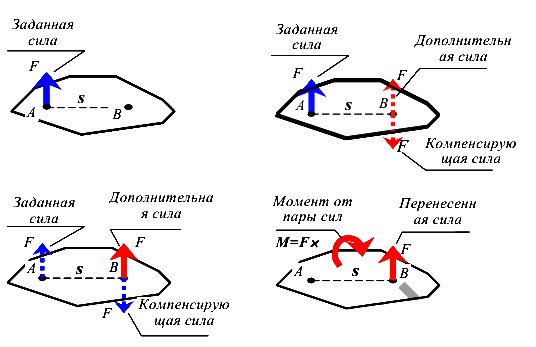
Очевидно, что в результате параллельного переноса силы появляется момент, равный произведению исходной силы на расстояние переноса.
То же самое проделаем и для внецентренно приложенной к колонне силы. Только в этом случае будем перемещать ее дважды (рис. 119). Вначале переместим точку приложения силы на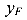 
, так, чтобы она оказалась на оси X, а затем на 
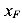чтобы она оказалась на продольной оси колонны Z. В результате такого двойного переноса появляются два момента — момент относительно оси X 
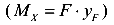и момента относительно оси У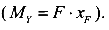 
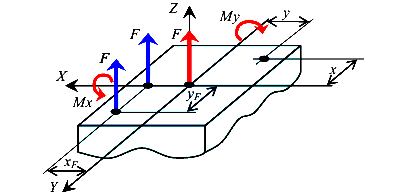
Для удобства рассмотрим внецентренно сжатый стержень прямоугольного поперечного сечения (рис.119). Это удобно, потому, что заранее известны положения главных центральных осей инерции, которыми будут оси симметрии сечения.
В результате такого переноса кроме центрально приложенной силы F появятся еще два момента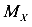 
и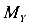 
. Так как эти моменты относительно поперечных осей, то они являются изгибающими.
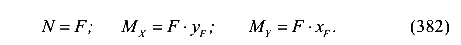
Таким образом, внецентренное растяжение (сжатие) приводится к трем простым видам сопротивления — центральному растяжению (сжатию) и двум чистым изгибам. Используя принцип независимости действия сил, вычислим напряжения в произвольной точке поперечного сечения стержня от каждого внутренней силы отдельно и сложим их.
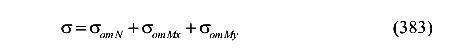
или
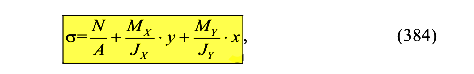
где N — продольная сила, равная внецентренно приложенной равнодействующей всех сил, приложенных к колонне N= ± F Если колонна внецентренно растянута, то принимаем знак «плюс», если внецентренно сжата, то принимаем знак «минус
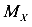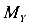, — изгибающие моменты, вызванные эксцентриситетом приложения равнодействующей силы
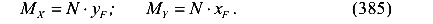
- А — площадь поперечного сечения колонны;
,
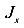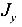главные центральные моменты инерции поперечного сечения колонны;- х, у — координаты точки, в которой вычисляется напряжение.
Под силой F следует понимать равнодействующую всех сил, приложенных к колонне.
Полученная формула, согласно принципу Сен-Венана, справедлива для сечений достаточно далеко удаленных от места приложения нагрузки. Сделаем преобразования и запишем эту формулу в другом виде.
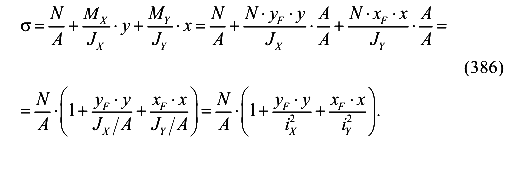
Окончательно имеем
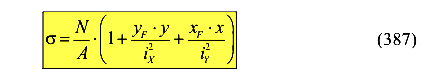
или
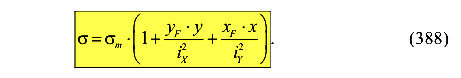
Здесь
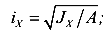
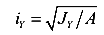— радиусы инерции поперечного сечения (являются геометрическими характеристиками сечения и измеряются в см, мм, м и т.д.);
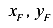— координаты точки приложения равнодействующей;- х, у — координаты точки, в которой вычисляется напряжение;
- N — продольная сила в сечении колонны;
- А — площадь поперечного сечения;
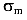— среднее напряжение в сечении колонны,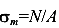 
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
