Оглавление:


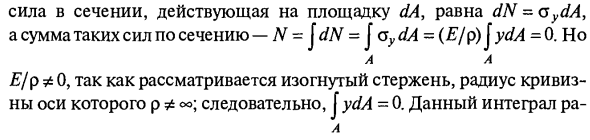

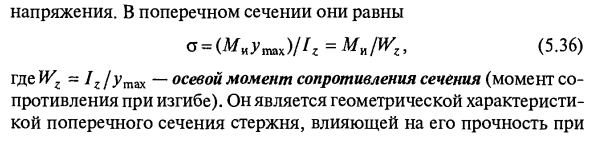



Определение нормальных напряжений при изгибе
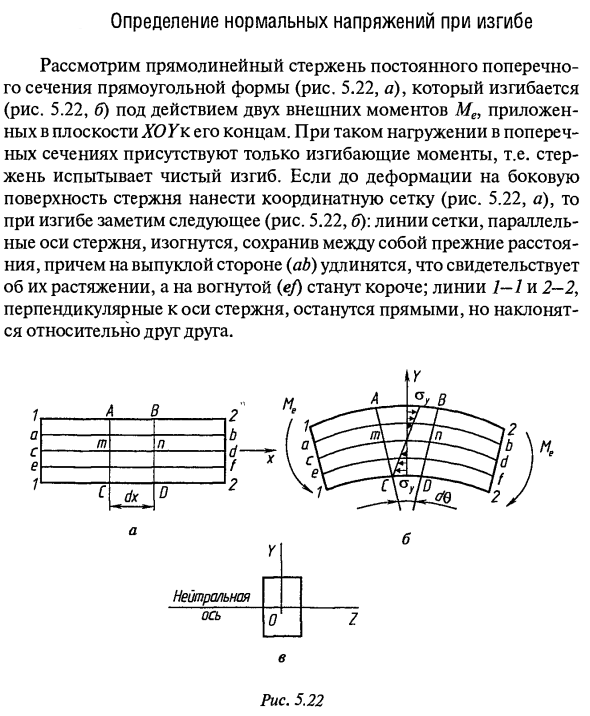
- Определение нормального напряжения при изгибе Рассмотрим прямоугольный стержень (рис. 5.22, а) с постоянным поперечным сечением, изогнутый под действием двух внешних моментов Me, приложенных к обоим концам на плоскости XOY (рис. 5.22, а). При такой нагрузке в поперечном сечении присутствует только изгибающий момент. Стержень изгибается чисто. Если координатная сетка применяется к стороне стержня до деформации (Рисунок 5.22, а), обратите внимание на следующее во время изгиба (Рисунок 5.22, б):
Он показывает удлинение и удлинение и становится коротким на вогнутой поверхности (ef). Линии 1-1 и 2-2, перпендикулярные оси стержня, остаются прямыми, но наклонены относительно друг друга. в Рисунок 5.22
Линии сетки, параллельные оси стержня Сохраняя одинаковое расстояние между ними, он может быть согнут на выпуклой стороне (ab). Людмила Фирмаль
Предполагается, что поперечное сечение, которое было плоским до деформации, остается плоским после деформации. При переходе от вытянутой части изогнутого стержня к сжатому стержню возникает слой (а /), в котором во время изгиба не происходит сжатия или растяжения. Это называется нейтральным слоем. Линия пересечения между нейтральным слоем и плоскостью Длина поперечного сечения стержня называется нейтральной осью. Как видите, деформация сердцевины волокна отличается.
Выберите стержневой элемент, окруженный двумя поперечными сечениями на бесконечно малом расстоянии dx друг от друга. При изгибе секции AC и BD будут вращаться под углом </ 9. Волокно m-nu, принадлежащее нейтральному слою (рис. 5.22, б), сохраняет свою первоначальную длину dx, а волокно AB, которое находится на расстоянии y от нейтрального слоя, имеет длину dx ‘. Можно считать, что радиус кривизны p дуги mn изогнутой оси стержня постоянен. Относительная деформация волокна £ _ dx’-dx _ (p + y) * / 9-p </ 9 _ y dx p </ 9 p Он прямо пропорционален расстоянию от нейтрального слоя. Где p — радиус кривизны нейтрального слоя (изогнутая ось).
- При чистом изгибе отсутствует поперечное напряжение на поперечном сечении стержня. Предполагается, что продольные волокна не спрессованы и подвержены одноосному растяжению или сжатию. Зависимости, полученные на основе этого предположения, дают результаты, которые хорошо согласуются с экспериментальными данными. Согласно закону Крюка, напряжение прикладывается к растяжению или сжатию слоя на расстоянии y от нейтрального слоя. ой = ес = ес / с. (5,32) Из уравнения (5.32) видно, что в нейтральном слое нет нормального напряжения и максимальное напряжение создается в волокне, наиболее удаленном от нейтрального слоя.
Напряжение, действующее в точке поперечного сечения, связано с внутренней силой поперечного сечения с помощью чистого изгиба. При использовании метода сечения не существует не только боковой силы Q, но и продольной силы N, т.е. N = Fa = 0. Элементарная вертикаль Сила поперечного сечения, действующая на участке dA, равна dN = oydA, а сумма таких сил поперечного сечения равна N = jdN = I GydA = (E / p) jydA = 0. но А E / p * O, поскольку изогнутый стержень учитывается, радиус кривизны его оси p f © o, поэтому J ydA = 0. Это интеграл
Однако, поскольку ни p, ни положение нейтрального слоя не известны, техническая формула (5.32) не используется. Людмила Фирмаль
Вена на статический момент Sz поперечного сечения относительно нейтральной оси (рис. 5.22, в). Поскольку он равен нулю, нейтральная ось (OZ) проходит через центр масс поперечного сечения (см. Раздел 5.11.1). Координата y в уравнении (5.32) получает определенность, она равна расстоянию до оси через центр тяжести сечения. Изгибающий момент сечения L / u = Me. Для заданной рабочей поверхности момента внешней силы Me изгибающий момент равен моменту внутренней силы в той же плоскости.
Против нейтральной оси. Изгибающий момент выражается основной внутренней силой dN. Допустимое направление оси, MPU = 0 и общий изгибающий момент = M »Z = \ ydN = (E / p) J y2dA = (E / p) Iz, (5.33) Где Iz = Jy2dA — момент инерции сечения относительно нейтрали. Ось; p — радиус кривизны искривленного нейтрального слоя. Выразим кривизну нейтрального слоя из уравнения (5.33). 1 / p = МДж (Efz). (5,34) Подстановка этого значения 1 / p в уравнение (5.32) дает зависимость Cy = M pU J11, (5,35) Это позволяет определить нормальное напряжение в любой точке поперечного сечения стержня с известным изгибающим моментом Mn и моментом инерции Iz поперечного сечения относительно оси, проходящей через центр масс поперечного сечения.
Из уравнения (5.35) видно, что нормальное напряжение нейтрального слоя равно нулю, когда}> = 0, а максимальное нормальное напряжение находится на самом дальнем волокне от нейтрального слоя, когда y = utax (рисунок 5.22). , Б). При расчете силы нас в первую очередь интересует Напряжение. Равный в поперечном сечении a = (Miutah) // r = Mi / W „(5.36) Здесь Wz to IJymzx — это момент сопротивления в осевом направлении сечения (момент сопротивления при изгибе). Это геометрическое свойство поперечного сечения стержня и влияет на прочность стержня
Перегибания. Для стержня с прямоугольным поперечным сечением со сторонами h и b (см. Рис. 5.16, а) момент сопротивления равен Wz = £ A2 / 6, а стержень имеет круглое сечение с диаметром d Wz = 0Дd * (рис. 5.16.6) , Несмотря на то, что уравнения (5.35) и (5.36) выводятся для чистого изгиба, было установлено, что надежные результаты могут быть получены при боковом изгибе. Условие прочности стержня постоянного сечения при изгибе при нормальном напряжении (Wz = const) является следующим: max = ^ itaxf ^ z adm, (5.37) Где oajm — допустимое растягивающее напряжение материала.
Mn max — максимальный изгибающий момент поперечного сечения по длине стержня, и его можно получить из рисунка изгибающего момента Mn = Mi (x). Используйте зависимости при выборе поперечного сечения изогнутого стержня maxadm- Размеры прямоугольного или круглого сечения определяются приведенными выше зависимостями. Для металлических профилей (двутавровая балка, канал, угол и т. Д.) Значение Wz отображается в ассортиментной таблице. Конечный изгибающий момент определяется следующим образом: Л / с <Wzoadm. Зная соотношение между L / I (/ и нагрузкой), вы можете найти максимальную или допустимую нагрузку при построении изгибающего момента.
Момент сопротивления Wz поперечного сечения стержня, который может выдерживать тот же самый предельный изгибающий момент, является одинаковым. Чем меньше площадь поперечного сечения стержня A, тем более рациональной является конструкция с точки зрения материальных затрат. для Обоснованность сечения можно оценить по безразмерной величине fVz / -jA *. Для кругов и квадратов, для каналов -0,57 … 1,35, 0,14 и О, 167, для двойного Т, 1,02 … 1,51. В дизайне мы работаем над наиболее рациональным использованием изгибов, двутавровых балок и каналов.
Смотрите также:
Решение задач по прикладной механике
Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.

