Определение непрерывного отображения

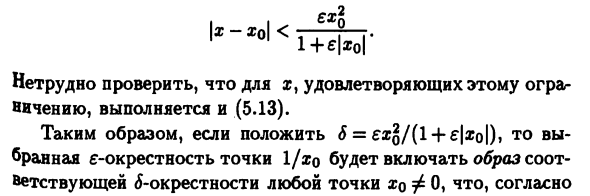
Определение непрерывного отображения

• f: X- \ Y — метрическое отображение X с метрикой p в метрическое пространство V Метрика d; a является пределом множества X. Определение 5.13. Карта /: X- + Y называется Продолжайте в € X (если €> 0) Поскольку δ = ε (ε)> 0, p (a, x) <6, χe » Запись 6 (е) подчеркивает, что 6 зависит от е. Определение 5.13 определяет, что такое электронная окрестность V = V (f (a), e) C точка f (a) € Y Y Непрерывность U = U (a, 6) a C X (например, f (U) C V) Если карта непрерывна в точке а, Вызывается непрерывные точки этой карты (Или эта функция).

В противном случае они говорят Отображение прерывистое (или функция прерывистая) Считается точкой а и называется разрывом карты (Function). Актуальная функция /: X- »СCR (значение R) Когда a∈X непрерывен (P (a, x) <6, x € X * \ f (x) -f (a) \ 0 36> Q: (| s-a | << J, x £ X ±> \ f (x) -f (a) \ Y называется Если есть ограничение, установите AcX постоянно Непрерыв непрерывно в каждой точке карты / a ‘—> A Набор последовательных функций в наборе A, Обычно указывается C (A). x e A C X и Карта / непрерывна в точке i, и эта карта ограничена Точка x на множестве A также непрерывна. Обратное дело не в этом Всегда верно Пример 5.5. Leuci b-set фиксированная точка Y, функция f (x) = b Vs∈X непрерывна Установите X.

В этом случае неравенство d (f (a)} f (x)) 0, точка x 6R присутствует. Людмила Фирмаль

Удовлетворяя неравенству | x -0 | <6} | »y (a:) — то (O) |> 1/2. Следовательно, функция m] (x) не является непрерывной Set R. Однако, например, определенные Работает с множеством [0,6], b> 0, Определения 5.12 и 5.14, m} (x) непрерывны в [0, 6]. Замечания 5.1. Вещественная функция f (x) Когда действительная переменная x∈R непрерывна в интервале [a, 6] Последовательный в интервале (а, 6) и двух граничных точках а и б. Интервал является открытым набором и включает в себя: Любой сосед этой точки. Поэтому рассмотрим (5.7) \ x-xo \ <6 * \ f (x) -f (xo) \ 0 3 ^> 0: Q ^ x-a <8 = * \ f (x) -f (a) \ a) \ (x, x0). (5.11) Действительно, если выбрано e> 0 и 6 = r, то Из условия p (x, x0) <ε, учитывая (5.11) \ f (x) -f (xo) \ = \ p (xy a) -p (x0, a) \ <e,

То есть, согласно определению 5.12, рассматриваемые функции Непрерывный в точке x0∈X. Где х0 В любой точке множества X эта функция непрерывна Каждая точка из X и определение 5.14 Непрерывно с определенным набором X. Особенно R Непрерывная действительная переменная действительная функция Если p (x, a) = \ x-a |, a = 0, функция p (x, 0) = (См. Рисунок 3.5). Пример 5.8. Действительные особенности (Если h = 1, см. Рис. 3.1) непрерывно в произвольной точке xΦ0 Номерная строка. На самом деле, любой Точка x0Φ0 и неравенство Хо хо (5,12) В Определите окрестности 1 / хо. непрерывность Функция f (x) в любой точке x0Φ0 = l / x Непрерывность R \ {0} на метрическом пространстве равна Q

• Если вы можете указать ^-соседство в этой точке, Условие (5.12) выполнено. С (5.12) Попытка получить лимит количества с той же конверсией | i-xo | Определить расстояние между точками x и xq. Явно желательно ^ • Соседи не должны содержать точку x = 0. В данный момент данная функция не определена. Это означает первое ограничение на такие окрестности Неравенство вокруг xq <| Да | (5,13) Ниже приводится 1 1 ла? -xo | \ x-xq \ la? -xq \ стоит? 0 ш | соа? | а? o (a? -a? o) + a? г | Из-за характеристик абсолютного значения числовое значение \ xq (x-xq) + jo | ^ | l? o- | a? о | • \ х-2? O || •

С точки зрения (5.13) 1-2 я-. Я l ll —2 | _ I i_ —I «L I 0 | | | | OM〜- • » ОI 0 | I *** *** 0 | * Берри | А? -Удовлетворить неравенство 1LC __L »L I _y. i ‘-i <£ (5-14) И условие (5.13), затем функция 1 / x, условие непрерывности (5.12) Φ0 выполняется в точке xq. Из (5.14) 1 + фоГ Это легко проверить? Встречайте это (5.13) верно. Так что если 8 = exl / (l + e \ xo ) Точка 1 / а? o выбранное электронное окружение содержит изображения Согласно определениям 5.13 и 5.14 соответствующая g-окрестность любой точки αФΦ0 указывает на непрерывность Функция f (x) = 1 / x на множестве R \ {0}. В частности, Замечание 5.1, эта функция Включает интервал (a, 6), интервал (-oo, 0) и (0, + oo) Сегмент [a, 6], не включающий точку x = 0.

Смотрите также:

Предмет математика

Замкнутые множества	Свойства непрерывного отображения множеств
Компактные множества	Линейно связные множества