Оглавление:







Определение напряжений в кривых брусьях
- Определение давления изогнутого стержня В различных конструкциях часто встречаются бруски с криволинейными осями. Они включают подъемные крюки, проушины, звенья цепи, шкивы и колеса, арки и т. д. Ось этих стержней представляет собой плоскую кривую. Полоса с осью пространственной кривой встречается редко и здесь не рассматривается. Правила определения их и построения
их участка для криволинейных стержней обсуждаются в§ 23. В§ 24 дифференциальная зависимость (3.13) — (3.15)оценивается между внутренним коэффициентом мощности и нагрузкой, в этой главе мы рассмотрим определение напряжений и смещений в стержне кривой, а также по выносливости. 431 он ограничивается рассмотрением стержней, имеющих вертикальную плоскость(фиг. 440), с которым и внешнее бремя действовать. Из-за симметрии движения точек оси луча эта плоскость также возникает. Исследования показали, что при изгибе распределение
нормального напряжения в поперечном сечении, а также величина Людмила Фирмаль
максимального напряжения криволинейной балки, отличается от балки с прямой осью. Другие равны, но эта разница больше, так как отношение высоты h поперечного сечения к радиусу кривизны его оси больше (рис. Четыреста сорок.) Пять. * ч я — =даю Т Г В связи с этой ситуацией принято различать брусок малой кривизны и брусок большой кривизны: при инженерных расчетах с бруском малой кривизны она возрастает до 3,5%, при — = = — | — она достигает 7%. Выведена формула нормального напряжения при изгибе балки
большой кривизны. Рассмотрим случай чистого изгиба криволинейных стержней (рис. 440). В случае прямого стержня мы сначала предположили положение неизвестного нейтрального слоя и выяснили, что он находится на уровне оси стержня. Здесь мы также предполагаем, что нейтральный слой в общем случае имеет неизвестный радиус кривизны GP, который отличается от радиуса R оси стержня. Вывод формулы напряжения изгиба осуществляется по той же схеме, что и для балок с прямой осью, и основывается
- на одной и той же гипотезе: гипотеза плоского сечения и гипотеза продольного волокна формируются друг на друге. Нарисуйте оси Y и z в поперечном сечении, как показано на рисунке. Ось Z в 440 фунтов совпадает с линией нейтрального сечения, и ее местоположение еще не определено. Берем направление оси y к центру кривизны луча. Для получения уравнения 432 криволинейная балка разрезается на две части с произвольным поперечным сечением. 440), и выделите участок DF элемента в разрезе, находящемся на расстоянии y от нейтральной
линии(фиг. 440 и 441, а). На элемент воздействует сила УДФ. Условия (10.2)и (10.3) из N-0, с M g=M и J adF-0; получаем £ oydF=M. F F F (15.1) Условие m u -) uzdF-0 автоматически удовлетворяется следующими условиями: Ф симметрии сечения относительно оси Y. Здесь вы выбираете из панели кривых (рис. 440) два бесконечно близких участка ab и CD основного участка, что соответствует углу деформации FR. После деформации угол между этими участками изменяется с некоторыми значениями D (dtp) (рисунок). 441, б). Наблюдая деформацию любого волокна AB, расположенного на расстоянии y от нейтрального слоя, и имеющего длину до деформации (B1—Y) DTP,
становится ясной длина любого волокна, выбранного из него взаимным вращением сечения AB и CD., РН-у Людмила Фирмаль
уа (фр)). (1 5.Два. ) F и z и h E S K s S t o r o n u, что касается пучка, если мы проигнорируем добавление * продольных волокон друг к другу, мы можем выразить формулу крюка: Если вы присвоите этому выражению выражение e, то, следуя выражению (15.2), вы получите ATE (FR)dq (15.3) Эта формула, по-видимому, не может быть использована непосредственно для определения нормального напряжения в чистом изгибе кривой стержня, а изменение угла D для определения gn и D (dq>) 433 из первого условия мы имеем. ED (dq), _ в этом выражении — — — — — f0, ttoo (15.4) Ф Второе условие записывается как C(dtp)f yMF соответственно.. (15.5) Интегрирование последнего уравнения можно записать следующим образом: (’»W G-g», g-S/g » и Г Ф (15.6) Первым интегралом в правой части уравнения (15.6) является
статический момент S2 площади поперечного сечения относительно нейтральной оси g, т. е. F (- e) (рис. 440, Б), а второй Интеграл равен нулю, согласно формуле (15.4). Учитывая это, выражение (15.6) можно записать в виде: (’5.7′) Где е-расстояние от центра тяжести поперечного сечения изогнутой балки до нейтральной оси, а F-площадь поперечного сечения балки. Очевидно, что Интеграл в левой части уравнения (15.7) всегда имеет положительное значение, а это означает, что статический момент Sz имеет отрицательное значение. Поскольку статический момент равен произведению положительного значения F, то координата e центроида области F относительно нейтральной оси z означает, что e всегда отрицательна. Поэтому при изгибе криволинейной балки можно утверждать, что нейтральная ось всегда смещается от центра тяжести поперечного сечения к центру кривизны балки. Кроме того, в выражениях,
содержащих e и Sz, мы имеем в виду их абсолютные значения. Если вы присваиваете выражение (15.7)условию (15.5), вы получаете Откуда Эд (рука помощи) JW4<Р например Учитывая формулу (15.8), формула для определения напряжения (15.3) может быть выражена следующим образом И= _ Г эф (РА^г)’ Или Мычать С2 (ру-г)’ Где M-изгибающий момент в сечении, а Sz-статический момент поперечного сечения изогнутой балки относительно нейтральной линии. Из анализа формулы (15.9) следует, что для балки с прямой осью нормальное напряжение по ширине сечения такое же (не зависит от z), а относительно высоты сечения по изменению расстояния точки от нейтральной линии напряжение изогнутой
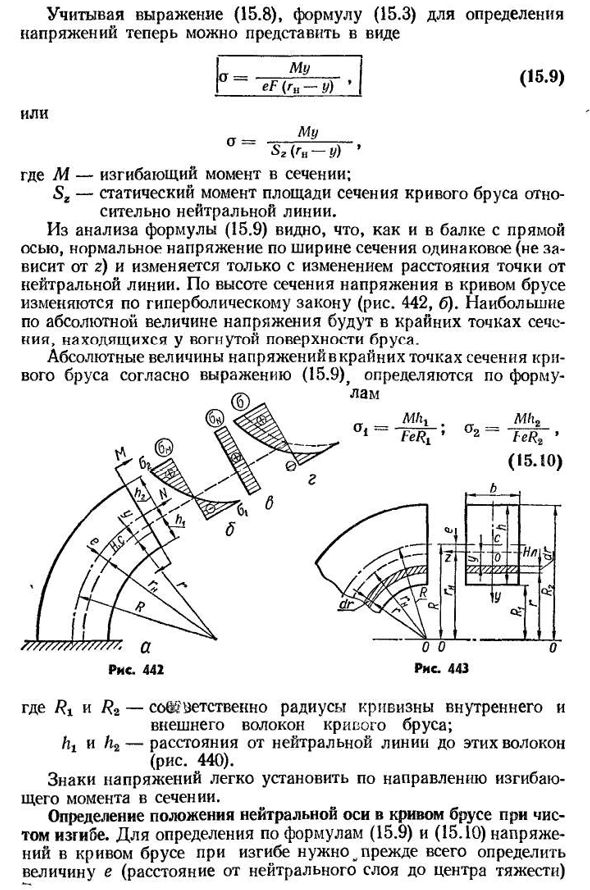
балки изменяется в соответствии с гиперболическим 442, б). Максимальное значение абсолютной величины напряжения лежит в крайней точке поперечного сечения, которая расположена на вогнутой поверхности балки. Абсолютное значение напряжений в крайних точках поперечного сечения криволинейной балки определяется по формуле (15.9) по следующей форме- Рис 442 рис. Четыреста сорок три Где Rt и R2-радиусы кривизны внутреннего и внешнего волокон изогнутого пучка, а ht и h2-расстояния от нейтральной линии до этих волокон(см. фиг. 440). Знак давления легок для установки к моменту изгиба в разделе. Определение положения нейтральной оси в криволинейной балке в момент чистого изгиба. Для определения по формулам (15.9) и (15.10)
напряжений изгиба балки при изгибе необходимо сначала определить величину е (расстояние от нейтрального слоя до центра тяжести) Радиус нейтрального слоя 435 равен е=я-Г», (15.11) Здесь R-радиус слоя, содержащего центр тяжести криволинейного сечения балки. Покажем, как определяется положение нейтрального слоя на примере бруска высоты h и ширины b прямоугольного сечения(рис. 443). Для этого мы исходим из уравнения(15.4): — ^ — = 0. г» — г Ф Это выражение вводит следующую подстановку переменных (рис. 443): g=GI-y, или y=GI-G. Тогда вы можете переписать уравнение (15.4) как C-well-dF=0, или GN (- — — — F=0, F Ф Откуда Ф Я G A~C dF’(15.12) Дж г Ф И я думаю, что Ф=ЧД, ДФ=БДР, У нас есть Шестьдесят один. — ЧД х х —••(15.13) С БСД) п — § −2,303 ЛГ. t «1» 1, где 2,303-модуль
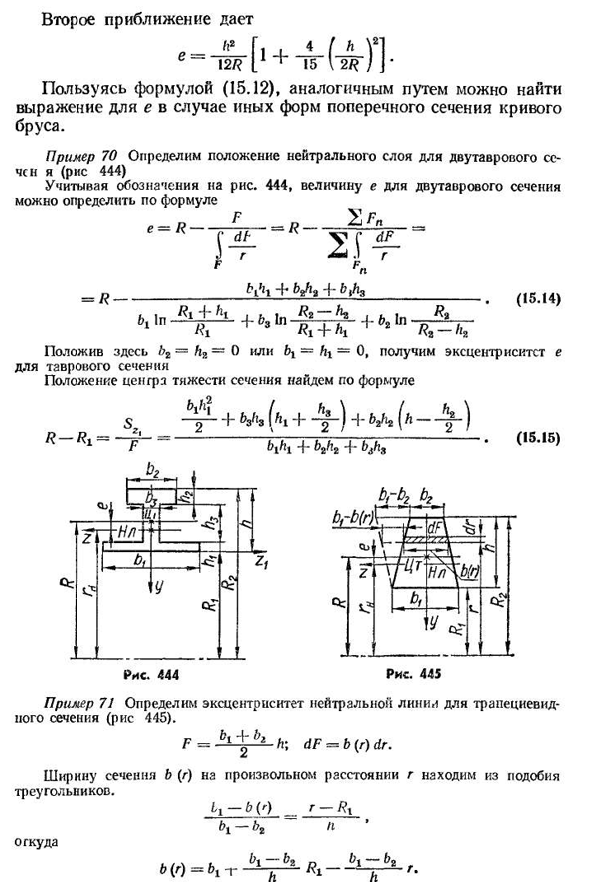
перехода к десятичному логарифму. Воспользуйтесь преимуществами близости 1П -?2 — =1П С 1+Г-2Г Я ——-— 2Р I, U получить е 1+ В первом приближении Р Четыре. И-К*¶ • Ла 12/? * /1 1 1 \ (■+Нет.)*) 436-е приближение является Аналогичным образом, используя формулу (15.12), можно найти формулу для Е в случае других форм поперечного сечения изогнутой балки. Пример 70I-определение местоположения нейтрального слоя относительно сечения (фиг. 444) дается обозначение на рисунке. 444, значение e I секции может быть определено по формуле e=R — — Р.————————— + +. (1 5 1 4 ). . / ?Х4 ″ ХТ. Р2 -/?2. Р2. Шесть. ^П1^+Б z_^^^^+/, 2 1Пл _ Здесь, если мы положим b2=h2=G или BX==0, то получим эксцентрик e секции t, а положение центра тяжести секции определяется следующей формулой(/h-|-
62/i2(h^1^1 4′ ^2^-2 4″ Пример 71 определяет эксцентриситет нейтральной линии в трапециевидном сечении (рис. 445). Ф.=.К+Л. г; ДФ=б (р)др. Ширина сечения b (d)на любом расстоянии g определяется из подобия треугольников. К-Б(0р-ГХ ВХ^2 Откуда Б (г)=ВХ-г Тогда 437. Р. Ра Б Б Ки Это нетрудно получить, разделив статический момент сечения относительно основания на площадь. Общая формула из(15. 16), ставим~0 или B2=0 и находим значение эксцентриситета треугольного сечения, которое расположено соответственно. Круговое пустое сечение(рис. Для.) 446) аналогично, мы можем получить Один. / 4/?2-d2+ / 4/? D2 4 (15.17)
Смотрите также:
| Контроль правильности решения статически неопределимой системы | Расчет на прочность кривых брусьев |
| О расчете пространственных рамных систем | Определение помещений в кривых стержнях |

