Оглавление:






Определение напряжений при кручении круглого вала
- Определение давления кручения круглого вала. A. С помощью графика крутящего момента мы можем найти величину крутящего момента в каждой секции вала. Чтобы найти напряжение, вызванное моментом сечения, используйте основной метод для решения проблемы сопротивления материала, который является методом
сечения. Но прежде чем приступить к решению поставленной задачи, рассмотрим результаты экспериментальных исследований.190 проверка прочности на кручение[глава XI 7ik (рис. 122)или меньше. Все генераторы вращаются на один и тот же угол y, и
Квадрат, приложенный к поверхности вала, искажается, превращается в гантели, то есть добавляется деформация сдвига. Каждое Людмила Фирмаль
поперечное сечение поворачивается относительно другого вокруг оси оси на определенный угол, называемый углом закрутки. Величина этого угла пропорциональна расстоянию между моментом и сечением. Концы остаются плоскими, а контуры всех деталей ровными- Радиус, приложенный к сечению кромки, не изгибается после деформации. Расстояние между соседними секциями практически не изменяется, то есть секции 1-1 и 2-2 вращаются
относительно друг друга на угол D4dz Ф-З.- 2/2 После деформации обе секции (1-1 и 2-2) вращаются относительно кромок, зажатых углами UX (секция 1-7) и (секция 2-2). Исходя из принятой гипотезы, оба сечения остаются плоскими, а радиусы 0% B и OHA, O^C и O2T) остаются прямыми линиями, и при этих условиях весь элемент ABDCO^O^соответствует сечению 2-2, его правая грань соответствует сечению 1-7. поскольку он вращается под углом DY, прямоугольник ABDC будет положением, показанным на рисунке. «Штриховка 124
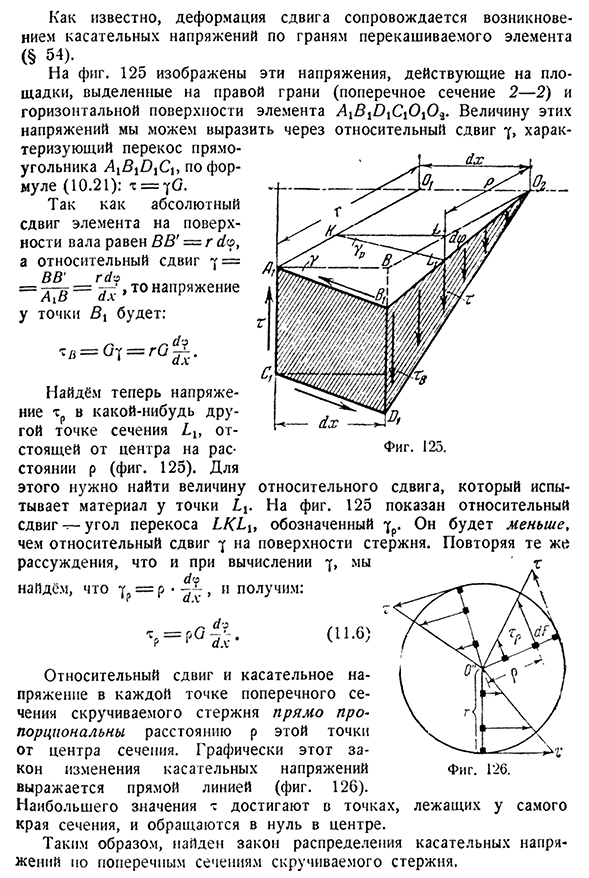
- » представляет собой косой элемент AHV^OHO, показанный на рисунке. 125; там же пунктирная линия показывает внешний вид этого элемента. Рассогласование, вызванное неравными вращениями секций 7-7 и 2-2, ABDC прямоугольные прямые углы превращаются в тупые и острые; наши элементы 122 и 124). Величина этой деформации характеризуется углом перекоса (относительным сдвигом).на поверхности прямоугольного стержня a^B^D ^ i этот угол равен VA^B^. 125 букв у.§ 57] определение напряжения кручения 193 Как известно, деформация сдвига сопровождается появлением
касательного напряжения на плоскости накачиваемого элемента (§ 54). Как использовать 125, эти напряжения, теризующие косой прямоугольник a^B^C^через уравнение (10.21)видно, что воздействующий на выбранную область справа от горизонтальной плоскости элемент напряжения может быть представлен в виде. Абсолютный сдвиг элемента на поверхности вала равен BB’=g dy, относительный сдвиг 7= В «ГСВ» = > напряжение в точке x равно:^ = GT=r O g. (Поперечное сечение 2-2) и a^B^B^C^O^o^эти относительные сдвиги y размер, Халак- Теперь найдем напряжение Tr в других точках поперечного сечения вдали от центра расстояния p(рис. 125). Для этого необходимо найти значение t-материала в точке
сдвига-t-угол наклона LKL^, чем относительный сдвиг 7 на поверхности стержня, и если вычислить 7, то вычисляется 7 p-p.•: Как Людмила Фирмаль
использовать 125 указывает на указанный y. он был Какой тестовый родственник будет меньше. Повторите то же самое (11.6) Относительный сдвиг и напряжение сдвига в каждой точке поперечного сечения скрученного стержня прямо пропорциональны расстоянию Р этой точки от центра сечения. Графически этот закон изменения касательного напряжения представлен прямой линией (рис. 126). Максимальное значение T — это точка сечения, которая достигает края и исчезает в центре. Таким образом, найден закон распределения напряжений по поперечному сечению крученого стержня. 7 и 11. М. Беляев С Фигура. G26 Находиться в кручении касательной напря-194. Проверка прочности[глава XI G. величина тангенциального напряжения может быть определена из уравнения (11.5), представляющего равновесное состояние отрезанной части.
Если вы подставляете это значение (11.6) вместо T, возьмите значение и возьмите константу при интегрировании области、: I p*dFf т. е. сумма произведения от базового участка на L расстояния до точки O называется полярным координатным моментом инерции и обозначается как Jp. Затем Где угол кручения (относительный угол кручения) на единицу длины вала равен: Y_m К dx-GJP * (11.7) Если вы присваиваете это выражению(11.6)、: (N. Восемь) Наибольшее значение напряжения получено в точке поперечного сечения осевой поверхности p=pm ax= = r: тахометр — * ^crth (11.9) ДЖП’ Выражение Ttah может отображаться в другом формате: Тонны — Кристалл. ДЖП Знак \Рмакс./ __L4K Вт-п — (11.10)) Отношение Wp называется во времена сопротивления Рот Поскольку момент инерции JP выражается в единицах четвертого порядка длины, то момент сопротивления WP измеряется в единицах кубической длины.
Смотрите также:
| Понятие о крутящем моменте | Вычисление полярных моментов инерции и моментов сопротивления сечения вала |
| Вычисление моментов, передаваемых на вал. | Условие прочности при кручении |

