Определение напряжений и проверка прочности при изгибе с кручением

Определение напряжений и проверка прочности при изгибе с кручением

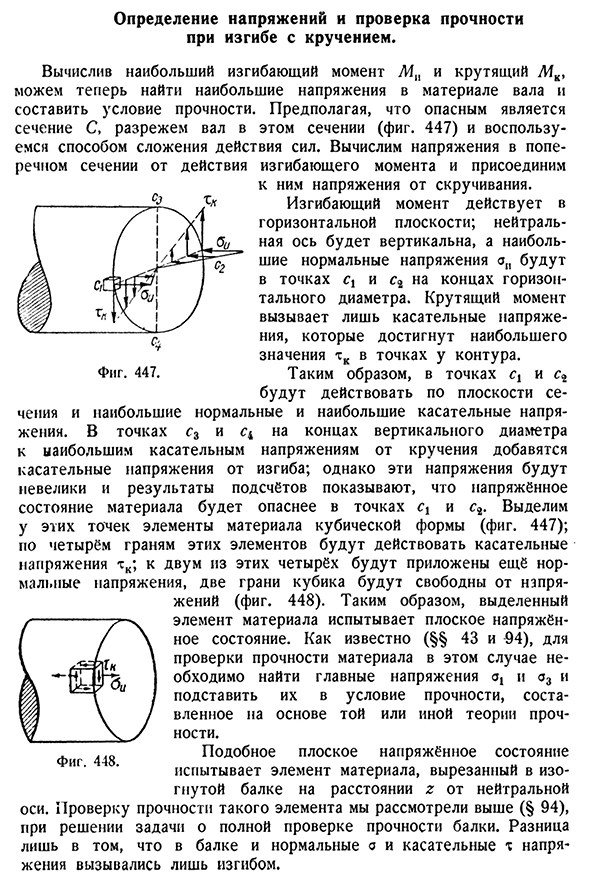
• Определение давления и проверка прочности на кручение и изгиб. В результате расчета максимального изгибающего момента L4N и крутящего момента 7IK теперь можно найти максимальное напряжение в материале вала и создать условия прочности. Предполагая, что член C опасен, этот член будет разрезать ось. 447) и использовать метод сложения силового воздействия. Рассчитайте и приложите напряжение поперечного сечения от действия

изгибающего момента Фигура. Четыреста сорок семь Напряжение от скручивания к ним. Нейтральная ось будет вертикальной, а максимальное вертикальное напряжение AP будет составлять точки cv и G2 конца горизонтального диаметра. Крутящий момент вызывает только тангенциальное напряжение, достигающее наибольшего значения TC в точках вблизи контура.

Так, в точках q и C2 действуют на плоскости CE-нормальные и максимальные касательные Людмила Фирмаль

напряжения на концах вертикальных прямых диаметров чения и Max Genin-G3 и C4. Однако эти напряжения становятся меньше, и результаты расчетов показывают, что напряженные состояния материала становятся более опасными в точках СХ и С2. В этих точках выделим элементы материала Куба(рис. 447); в четырех плоскостях этих элементов действует касательное напряжение TC; два из этих четырех или более нормальных напряжений будут

безнапряженными на двух плоскостях Куба (рис. 448). Таким образом, выбранные элементы материала испытывают плоскостно-напряженное состояние. Как известно (§ 43 и 94), для того чтобы проверить прочность материала в этом случае, необходимо найти основные напряжения Oj и A3, которые создаются на основе конкретной теории прочности. Аналогичное плоское напряженное состояние испытывают материальные элементы, разрезанные на балки, изогнутые с z от нейтральной оси. При решении задачи полной проверки прочности балки, проверьте прочность таких

• элементов, как мы рассмотрели выше(94). Единственное отличие состоит в том, что в балке как обычные а, так и касательные Т напряжения были вызваны только изгибом.§ 167] определение напряжений и проверка прочности 513 (28.1) Чтобы проверить прочность отсоединенных элементов от вала, подставляя значения A и t вместо a и T в AI и TC, непосредственно применяя формулу, полученную в§ 94, затем получая следующие условия прочности (согласно теории четырех): теория максимального вертикального

напряжения.: / Теория максимального удлинения: [0.35 AI+ 0,65 / 4 + 4 4 ] < [а]. Теория максимального касательного напряжения: 4 ″ 4Т/[а]. Энергетическая теория: / 4 + 3 4 [а]. Чтобы связать это испытание на прочность со значениями моментов 7IK и Afj и размерами вала, необходимо рассчитать напряжения AI и TC. Напряжение AI равно изгибающему моменту M и максимальному нормальному напряжению при Здесь вал круглого сечения W=; буква g обозначает радиус поперечного сечения вала. С другой стороны, максимальное напряжение при кручении вала TK равно 7К АФК АФК М К ТС-WР—2Вт* 2 4 Подставляя эти значения напряжений в первое

уравнение (28.1), получаем следующее уравнение: < 7л Ф/М «+ / Л О ш УЗ’ -!- 4W7 » J-2W — Аналогично можно получить расчетную формулу для других Людмила Фирмаль

теорий прочности. Легко видеть, что все эти функции могут быть заменены одной: (28.2) g de2ir-расчетный момент. 17Н. М. Беляев №. — Кручение+v514 совместное действие I изгиб[гл. XXVllt Из теории ми и МВ, а также принятой силы. Он равен teo * RII самое высокое нормальное давление: Φ4º1=1 [TRL4-V mi+теория самое большое удлинение: M p i=MV0, 35+0,65 M l+M i, в теории, самое большое напряжение сдвига можно измерить.= 1 < < 4 — 0,7 5 мл- (28.3) Формула (28.2) структурно идентична формуле для испытания на прочность нормального напряжения изгиба по моменту L4r.

В некоторых конструкциях, помимо скручивания и изгиба, вал растягивается продольной силой, или он подвергается этим силам относительно прочности вала, подлежащего сжатию. Из Формулы(28,2) получаем Около /— 4[а]’ Таким образом, радиус вала равен d=<2r(28.4) для использования этой формулы необходимо только установить, какую теорию прочности следует использовать, и, следовательно, формулу для вычисления расчетных моментов (28.3).） Поскольку валы обычно изготавливаются из пластичного металла в стали, теория максимального вертикального напряжения

исчезает сразу же после выбора теории прочности (см.§ 43). До сих пор в машиностроении использовались формулы, основанные на второй теории (Максимальное удлинение), иногда называемой формулой Сен-Венана: [0, 35M и 4-0, 65 Y M l+M ij[a], несмотря на то, что для пластического металла эта теория, безусловно, неверна; в последнее время не было никого для расчета. По четвертой (энергетической) теории-мул, или на основе третьей теории (максимальное тангенциальное напряжение: I4G^UI2+° ’ 75M^M- В таблице 25 сравниваются результаты определения диаметра вала в различных соотношениях 2ii и 7IK при одинаковых допустимых напряжениях с учетом различных теорий прочности. Значение диаметра (формула St-Venant), полученное с применением теории наибольшего

удлинения, было принято равным единице. Сравнение диаметра вала T A b l I C A25. Отношение М До ми* Диаметр вала при применении П Теория III Теория _ВНУТРИВЕННЫЙ Теория АФ » =О1 1 1,15 1,10 1,07 1,03 М N=М К1 1.03 1.01 Из этой таблицы, прежде всего, видно, что разница в размерах валов относительно невелика, в зависимости от выбора теории. Это может объяснить тот факт, что на практике выражение Сен-Венана иногда все еще используется, но оно основано на теории, которая явно не подходит для используемого материала. Практические инженеры, переход к расчетам по новой формуле, основанной на более точной теории, если бы сохранялись старые нормы допустимых напряжений, потребовали бы установки вала большего диаметра, что фактически сделало бы расчет по старой формуле Сан-Венанта благополучно отработанным синнахшафтом.

Решение проблемы заключается в том, что при переходе на новую формулу невозможно поддерживать тот же коэффициент запаса, который является тем же допустимым напряжением. Для повышения точности расчетов и углубления знаний о работе материалов, как правило, необходимо уменьшить коэффициент запаса и увеличить допустимое напряжение [а]. Поэтому, чтобы ввести расчет момента по новой формуле на практике, необходимо убедиться, что диаметр вала, работающего безопасно, достаточно надежен при новом методе расчета.

Смотрите также:

• Примеры решения задач по сопромату

Ядро сечения	Вычисление напряжений и деформаций.
Определение изгибающих и крутящих моментов	Расчёт простейшего коленчатого вала