Оглавление:






Определение коэффициентов массопередачи при малых скоростях массообмена
- Во многих системах, где происходит массоперенос, существуют градиенты концентрации по обе стороны границы раздела. Рассмотрим двухфазную жидкостную систему в качестве простого примера. Содержание этого раздела совпадает с содержанием оригинальной работы вплоть до нотации [10]. Газ состоит из смеси газов 4 и в, контактирующих с нелетучей жидкостью С, причем жидкость с предполагает, что она может поглощать только вещество А. Профили концентрации для обеих фаз этой системы показаны на рисунке. Показана молярная доля вещества а в газовой фазе через 20-6. Что такое межфазное сопротивление способ Массоперенос определяется приемом.Границы ничтожны.
Экспериментальные данные, которые являются показанными предположениями, весьма обоснованы для многих реальных систем. Исключение составляют системы накопления примесей поверхностно-активных веществ на границе раздела фаз, а также системы с чрезмерно высокими скоростями массопереноса. В данном разделе описываются только такие случаи массопереноса, когда поверхностное сопротивление не играет существенной роли и пульсирующие компоненты турбулентных концентрационных полей каждой фазы очень малы. Следовательно, среднее по времени*значение молярной доли *В приведенном ниже тексте все величины считаются часами. Для краткости-знак усреднения (верхняя планка), k. It это невозможно сделать.
В пограничных слоях, окружающих ракеты, летящие с высокой сверхзвуковой скоростью, температуры могут быть такими высокими, что воздух ионизируется, в результате чего и атомы и молекулы станут электрически заряженными. Людмила Фирмаль
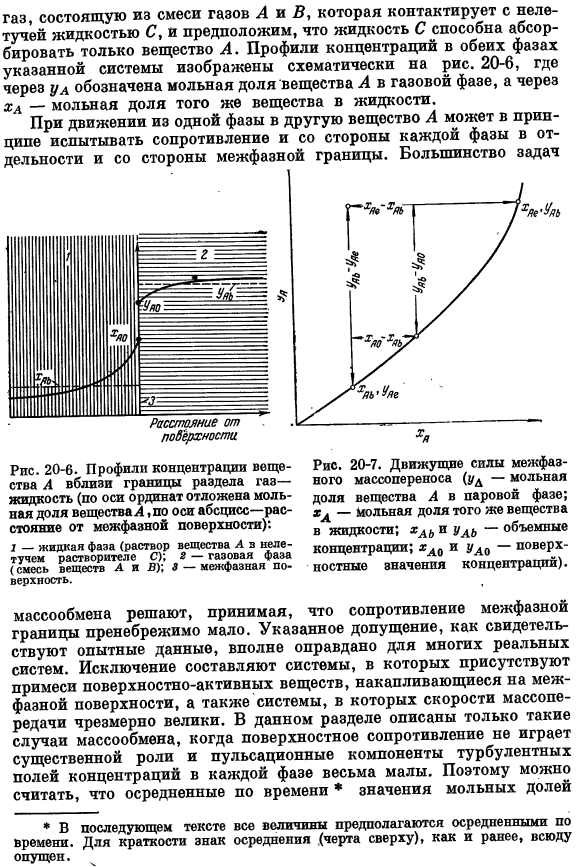
Интерфейсы St и xA удовлетворяют соотношениям равновесия. (20.51)) На〜/ (*Ло) На рис. 20-7 показаны типичные кривые равновесия и точки, соответствующие значениям равновесия YA и xA на границе раздела фаз. Разность между объемными и поверхностными значениями концентрации материала а на каждой фазе может быть выражена локальными значениями скорости массопереноса и коэффициента массопереноса на этой фазе.
Из уравнения (20.10) следует, что если фазовый переход 1 вещества а в жидкой и газовой фазах медленный, то уравнение (20.52) (20.53)) Локальный поток вещества NAₓ₉ в жидкую фазу (определяемый формулой nax₀ = DWF ^ LDA) из соотношения (20.52), локальный поток того же вещества из газовой фазы (характеризуемый формулой-naᵣ₉—DW ᵣ da/ da) точно равен. (20.53), производными dWAm ^ / dA и dWAIdA можно управлять out. As в результате получаем следующее уравнение: Формулы (20.51)и (20.54) могут быть использованы для вычисления 2 неизвестных величин ya₀ ха₉ и хА₉, если известны объемная концентрация и коэффициент массопереноса каждой фазы.
Если известны поверхностные концентрации yA₉ и xA₉, то скорость локального массопереноса можно рассчитать по формулам (20.52) и (20.53). Попытки экспериментального определения локального коэффициента массопереноса сталкиваются с большими фундаментальными трудностями, связанными с отсутствием методов непосредственного измерения поверхностных концентраций. Обычно такое решение может быть принято только в том случае, если разница в концентрации транспортируемых веществ в одной фазе незначительна по сравнению с соответствующей разницей в другой.
Для удобства представления экспериментальных данных часто используются так называемые коэффициенты массопереноса Kx и Ku, которые определяются соотношением, аналогичным формулам (20.52)и (20.53). used. So … Например, если материал а переносится в отсутствие материала, то мулы для вычисления коэффициентов Kx и Ku являются: 1 -?Л — К; — — — — — да — — — » л.- Вася(20.56) Где ole представляет собой объемную концентрацию материала A в газовой фазе, равновесное распределение между жидкостью и газом, а объемная концентрация в жидкой фазе задается xal.
- То есть величина ulg удовлетворяет соотношению yAe = / (xl), rppp-равновесная функция, которая фигурирует в уравнении(20.51). Определяется также концентрация xLe, удовлетворяющая уравнению Pd,= /(l.). Смысл УЛГ и значения ГВУ, показанную на Рис. 5. 20-7. Связь между коэффициентами Kx и Ku и коэффициентами массопереноса может быть установлена на основе следующих очень простых математических расчетов: в виде суммы 2 движущих сил представьте себе»среднюю движущую силу»массопереноса в газовой фазе, равную (ulg-yi). (УЛ-УЛ)=(УЛ, — УЛ.) +(УЛ, — УЛ)=’ = — *ло))^ ло!
В значение ty-это наклон линии, соединяющей истинную точку на линии равновесия (ul, do) с фиктивной точкой(ul «>д»).Это необходимо для расчета средней движущей силы газовой фазы. Здесь соответствующая левая часть уравнения (20.52) и (20.53) заменяется правой частью (20.57) вместо разности (xl-hao) и (Wao-Ul) и представляет движущую силу (YLE-ul) через коэффициент Кч с использованием соотношения (20.56).Если разделить обе части полученного выражения с Жва ха = = —dWAV Бней, вы получите*. После выполнения аналогичной операции с движущей силой (ha,-Chl) найдите зависимость между коэффициентом H И коэффициентом массопереноса.
Уменьшение плотности, которое в обычном газе связано с увеличением температуры, заставляет эти слои подниматься и таким образом создает поток свободной конвекции, переносящий тепло от объекта. Людмила Фирмаль
Где символ tx обозначает наклон линии, соединяющей точку (yA₀,lo lo) с точкой(yAb, xAe).Если линия равновесия является прямой и характеризуется наклоном, равным t (то есть tx = ti = t), то, как видно из формул (20.58) и (20.59), уравнение* (20.60) Это соотношение еще раз подчеркивает, что коэффициенты Kx и Ki имеют одинаковую информацию о передаточных характеристиках системы. При рассмотрении двухфазной системы, в которой происходит массоперенос, очень важно знать индивидуально, насколько общее сопротивление массопереноса падает в каждой фазе. Среднее сопротивление массопереносу паровой и жидкой фаз определяется уравнениями (20.58) и (20.59) соответственно.
Из них видно, что с увеличением локальных коэффициентов kx и ku сопротивление, оказываемое любой фазой, уменьшается с увеличением концентрации вещества A в этой фазе. phase. So, особенно для нахождения коэффициента массопереноса, эксперименты очень эффективны, так как 1 обменная фаза содержит почти чистое вещество А. Если коэффициент м очень велик (то есть если вещество А слабо растворено в жидкости С), то большая часть общего сопротивления массопереносу находится в жидкой фазе, и наоборот. Полученное выше соотношение можно легко обобщить при переносе 2 или более компонентов (см. задачу 20-6).
Большинство литературных данных, связанных с массопереносом в системах жидкость-газ и жидкость-жидкость, представлены в виде коэффициентов массопереноса или в виде величин, которые так или иначе связаны с этими коэффициентами. Подробная таблица экспериментальных результатов по массопереносу и краткое изложение известных корреляций средних коэффициентов массопереноса имеются в литературе[1-31. В области теории и практики двухфазного массопереноса в системах с подвижным интерфейсом существует множество нерешенных проблем.
Они обусловлены очень сложными гидродинамическими условиями, которые реализуются в большинстве систем жидкость-газ и жидкость-жидкость, невозможностью отбора проб непосредственно с движущейся поверхности раздела и отсутствием надежного способа расчета поверхности контакта фаз. Описание многих систем, встречающихся на практике, очень затруднено из-за наличия химических реакций, протекающих в жидкой фазе.
Смотрите также:

