Определение коэффициентов по методу Эйлера

Оглавление:

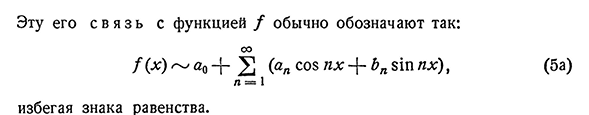
Определение коэффициентов по методу Эйлера — Фурье

Определение коэффициентов методом Эйлера-Фурье. Для установления возможности декомпозиции тригонометрических функций (5) для заданной функции/(x), если она имеет длительность 2ts, то задается некоторый коэффициент A0, который должен исходить из A0A0.. Вторая половина XVIII века показывает, как их определять,

что применялось Эйлером и независимо от него в начале XIX века Фурье. Здесь мы принимаем функцию/(x) последовательно или кусочно с интервалом[-TS,TS]. Намеренно интегрируем d o n u STI m, где происходит разложение(5), от-TS до TS. Но как легко увидеть, С 81P рН п\Соз р ч н ых=- — — — — — — =О3 п| — 7г И (6) Ы• — SO8p у Х Л Л\$\ДГПЖ г х= ————= 0 . л п\ — к397]§1. Введение 375

Таким образом, все члены под Людмила Фирмаль

знаком суммы будут равны нулю,и в конце концов мы узнаем л А о=4? \/(х)х. (7) — ТК Для того чтобы установить значение коэффициентов в,умножим обе части равенства(5),мы должны все время П Р Е Д П О Л А Г А Е М бежать,и снова на поп т х.: Первый элемент справа больше не виден в поле зрения (6). Тогда te81P px POPs t x=u u[z1P (I t)x+81p (I-ot)x] s1x=0, (8) — * te te Te POPs px POPs t x y x=~§[POPs (l/I) x s o z (p-t) x] (1x=0, (9) — te-Te-if p/l, наконец te S9 1 S1+2/— \ —— 2——-Ох. (10)-тэ-тэ таким образом,все интегралы под знаком нулевой суммы, кроме

интеграла, где множителем является коэффициент. Итак, этот коэффициент определяется: te at= — ^ — ^/(x) s o z t x y x (LG=1, 2, 3,…да что с тобой такое? (11) — Их Аналогично, если разложение (5) умножить на zsh/LX и проинтегрировать почву, то коэффициент определяется по синусу:te LT=—S/(x) 81P Exx(o t=1, 2, 3,…да что с тобой такое? •/ — Я. .. (12) 376ЧАП. XXIV. серия Фурье / 397 В то же время, в дополнение к (6)и(8), мы полагаемся на легко проверяемые соотношения: (13) в случае p f t、 (14) Формулы (7), (11) и (12) известны как уравнения Фурье масленка;коэффициенты, вычисленные по этим формулам, называются коэффициентами Фурье заданной функции, а с их помощью-коэффициентами Фурье. Ряд Фурье мы будем

рассматривать исключительно в этой главе. Давайте теперь рассмотрим логическую ценность рассуждений. (5) вопрос о том, соответствует ли это действительности, конечно, касается вас, потому что я предполагал, что тригонометрическая факторизация будет иметь место. Однако, следуя примерам Эйлера и Фурье, даже предполагая, что он работает, есть соображения, которые определили коэффициент разложения (5) убедительности? Серия N I e m использует p o h len n s m I n t e g R I r o неоднократно, и эта операция не всегда приемлема[n°269]. Достаточные условия ее

применимости является Р А В Н О М е р н а я в ы х о д И М о ст серии. Поэтому, если функция/(x) разлагается с p a в сходящемся тригонометрическом (5), последний должен быть его ряд Фурье. Заметим, что умножение всех членов ряда на ограниченные функции Pop TX, ZT TX поддерживает равномерную сходимость. Если мы не будем заранее предполагать однородность сходимости, мы даже не сможем доказать,

что функция может разложить t o l K o в ряд Фурье. В чем смысл вышеприведенных соображений? Их можно Людмила Фирмаль

рассматривать только как n A b e d e n I e, достаточные для того, чтобы начать с ряда Фурье для треугольного разложения данной функции (уже все) сходиться и далее устанавливать условия, при которых она находится в этой функции. Если это не сделано, мы имеем право рассматривать ряд Фурье данной функции/(x), за исключением того, что он»порожден»функцией/(x) 398]§1. Введение 377 Это он во мне?? Функция / обычно указывает на это: ООО /(сек)~А0 — {-2(п S08p ч+ч п) (5А) Р=1 Избегайте знака равенства

Периодические величины и гармонический анализ	Ортогональные системы функций
Интеграл Фурье как предельный случай ряда	Постановка вопроса. Интеграл Дирихле