Оглавление:





Определение касательных напряжений при изгибе
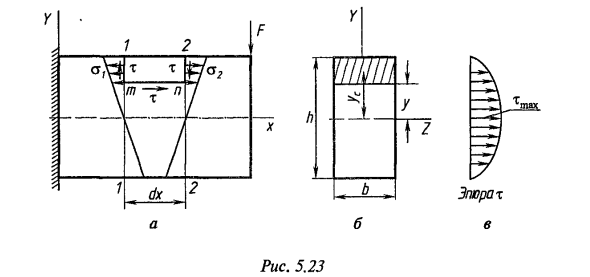
- Определение напряжения сдвига при изгибе. В случае поперечного изгиба поперечного сечения поперечная сила Q действует в дополнение к изгибающему моменту. Рассмотрим стержень, который прикреплен к одному концу (рис. 5.23, а) прямоугольного поперечного сечения и имеет сосредоточенную силу F, приложенную к свободному концу. Размеры сечения: высота А, ширина б. Выберите основной объем 1 mn2 с двумя поперечными сечениями 7- и 2-2, разделенными расстоянием dx и горизонтальной плоскостью mn на расстоянии y от нейтральной оси.
Он считается равномерно распределенным по всей ширине b. Вдоль плоскости 2n нормаль с2 = (Л / И2У)! Из и тангенциальное т напряжение (Мн \ а L / и 2 — изгибающие моменты сечений 1-1 и 2-2, а Iz — момент инерции поперечного сечения относительно нейтральной оси (OZ). Вдоль плоскости mn только касательное напряжение m равно касательному напряжению вертикальной плоскости согласно закону спаривания.
На этот элемент действуют следующие силы: 1m вдоль плоско-нормального напряжения = (Л / ˆ1y) / Iz и неизвестного касательного напряжения m. Людмила Фирмаль
Нормальный результат сечения 1-1 Внутренняя составляющая силы 1-1 ^ A = j = JC \ dA9 Нормальный результат сечения А ‘ ny 2-2sil N2 =] GidA, где A ‘- площадь вертикальной плоскости А ‘ Объем делится на площадь поперечного сечения. Уравнение баланса для силы, действующей на выбранный объем в виде выступа по продольной оси, имеет вид = —N \ + 7V2 + xbdx -0, (5.38) Где tbdx — сила, действующая на плоскость mt, связанная с напряжением сдвига. Из уравнения (5.38) это становится следующим. Tbdx = N {-N2 = JG \ dA -Jo2dA = «А» = (M »1 / Iz) lydA- (MH2 / Iz) \ ydA = (dMJIz) S’z, (5.39) «А» Где dMH = MH1-MH2 — приращение изгибающего момента по длине стержня.
dx \ Iz — момент инерции сечения относительно нейтральной оси. S’z — статический момент отрезанной части сечения относительно нейтральной оси. Выразите m из формулы (5.39). z_dM „S’z dx lzb Учитывая зависимость производной dMH / dx, равной боковой силе Q (5.31), существует уравнение Журавского для определения напряжения сдвига. х = QS’z / (изб). (5,40) Поскольку оставшееся количество формулы сечения (5.40) является постоянным, распределение напряжения сдвига по поперечному сечению стержня любой формы определяется законом распределения статического момента Sz.
- Рассмотрим изменение m стержня с прямоугольным сечением (рис. 5.23, б). Статический момент OZpuBcnS в области штриховки относительно нейтральной оси ^ = b (h / 2-y) yc = b (h / 2-y) ~ 0,5 (L / 2 + y) = 0y5b (h2 / 4-y 2), Здесь = 0,5 (L / 2 + >>) — расстояние от оси OZ до центра тяжести отрезанной секции. Это параболическое уравнение. Для Iz = bh 3 / l2 тангенциальное напряжение определяется уравнением (5.40).
Для стержней с прямоугольным поперечным сечением напряжение сдвига в 1,5 раза превышает напряжение, полученное, когда напряжение сдвига равномерно распределено по всему сечению. Напряжение сдвига tmax при изгибе является максимальным для нейтральной оси и других форм поперечного сечения.
Постройте диаграмму напряжения сдвига (рис. 5.23, в) в 3 точках: m ^ L / 2 = m ^ -A / 2 = 0; mu = 0 = 1 $ 0 / A Максимальное касательное напряжение в сечении действует на уровне нейтральной оси. Людмила Фирмаль
Tmax = — для стержня с круглым сечением, для стержня с кольцом 3 А Сечение tmax = 2 Q / A Условие прочности стержня при изгибе вдоль тангенциального напряжения имеет вид tmax <xadm. Где xadm — допустимое напряжение материала стержня на сдвиг или сдвиг. Обратите внимание, что касательное напряжение в сечении изогнутого стержня намного меньше нормы. Поэтому расчеты прочности обычно выполняются с использованием нормального напряжения в соответствии с уравнением (5.37) без учета влияния боковых сил.
Смотрите также:
Решение задач по прикладной механике
Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.

