Оглавление:




Определение гармоник ряда Фурье графическим (графоаналитическим) путем
Определить гармоники рядов Фурье графическими методами (графовый анализ). Графический метод определения гармоник ряда Фурье основан на замене конкретного интеграла суммой конечного числа членов.
- Для этого период функции f (x) t, равный 2n, делится на n равных частей Ax n. По определению постоянной составляющей является Ap («P» для «H» S 4 «• p-1 или A = YS fp W- <8’5) P-1. P — текущий индекс.
а интеграл заменяется суммой Людмила Фирмаль
От 1 до l Fp (x) — значение функции f (x) значения x = pDx, амплитуда синусоидальной составляющей k гармоник ряда = ~ Jf wsin kxdx ~ 2 • w ~ sinpkx ‘0 p-1 или Л = — ~ Sf₽w sinpkx-c8-6) • p-1 k амплитуда гармонической составляющей косинуса (8-7) pl, где sinp £ x и cosp kx равны x = p & x
Значения функций sin kx и cos kx, обычно при делении по формулам (8.5) — (8.7), делении периода на n = 24 или 18 частей и, возможно, даже на меньшее количество частей Достаточно проверить, не является ли разложенная функция не симметричной относительно осей, прежде чем выполнять графическое разложение на ряд (см. §169).
- Тот или иной тип симметрии Из-за наличия Следовательно, если кривая f (x) симметрична относительно горизонтальной оси, постоянная составляющая Ao и все четные гармоники отсутствуют, а нечетное k A * и При вычислении A * значение суммы (x) sinp kx в первой половине равно сумме 2! JZp (x) sinp £ x во второй половине.
Знак угла в уравнении (8.4) зависит от знака Ak и *. При создании гармоник в общем графике необходимо учитывать, что масштаб вдоль горизонтальной оси k гармоник [k
должен быть больше, чем первая гармоника. Людмила Фирмаль
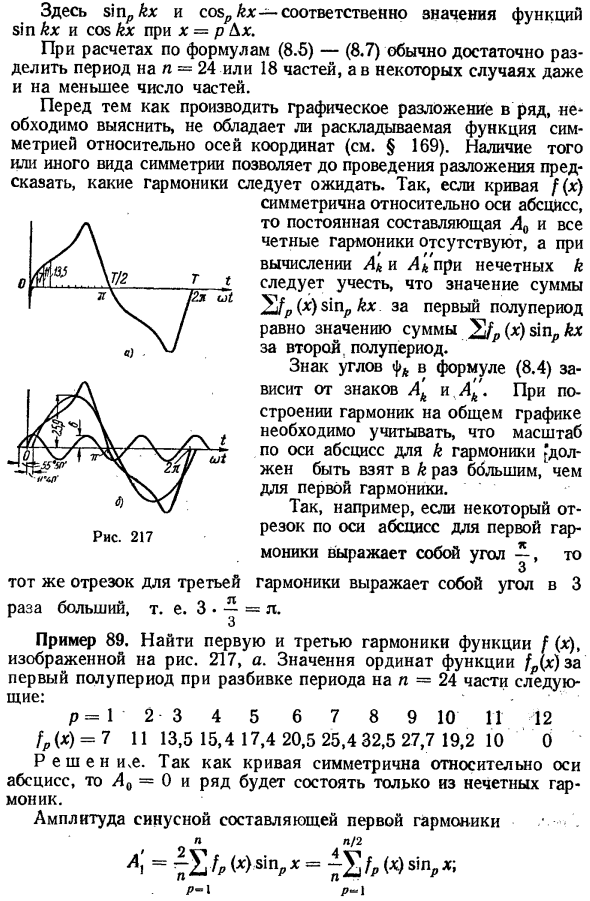
Например, если конкретный сегмент вдоль горизонтальной оси 1-й гармоники представляет угол, то тот же сегмент 3-й гармоники представляет 3-кратный угол, то есть 3 • ~ = l. Найти первую и третью гармоники показанной функции f (x): 217 a — отношение первой половины периода, когда период разделен на n = 24 части
Ордината / p (x) выглядит следующим образом: p = 1 • 2 3 4 5 6 7 8 9 10 11 12 / p (x) = 7 11 13,5 15, 4 17,4 20,5 25,432,5 27,7 19,2 10 0 Поскольку кривая решения симметрична относительно абсциссы, Ло = 0 и ряд состоит только из нечетных гармоник.
Амплитуда синусоидальной составляющей первичной гармоники равна nn / 2 A, = fp ( х) грех, Х = ^ фп (х) грех, х. pl l = A (7 грех 15 ° + 11 грех 30 ° + 13,5 грех 45 ° 4-15,4 грех 60 ° + 4- 17,4 грех 60 ° 4-20,5 грех 90 ° 4-25,4 грех 105 ° 4 32,5 грех 120 ° 4-4-27,7 грех 135 ‘4-19,2 грех 150 ° 4-10 грех 165 °) = 25,3.
Амплитуда косинусной составляющей первой гармоники l / 2 4 ‘= «S fp (x) cospx; P〜1 A» = A (7 cos 15 ° 4-11 cos 30 ° 4-13,5 cos 45 ° 4-15,4 cos 60 ° -f-4-17; 4 cos 75 ° 4-20,5 cos 90 ° 4- 25,4 cos 105 ° 4- 32,5 cos 120 ° — | -4- 27,7 cos 135 ° 4- 19,2 cos 150 ° 4-10 cos 165 °) = -5,23
Амплитуда синусоидальной составляющей третьей гармоники A’3 = ^ ifp w sinpxx = pl ■ = A (7 грех 45 ° 4-11 грех 90 ° 4-13,5 грех 135 ° 4-15,4 грех 180 ° -f- 4 -17,4 грех 225 ° 4-20,5 грех.270 ° 4-25,4 грех 315 ° 4-32-32,5 грех 360 ° 4-27,7 грех 45 ° 4-19,2 си 90 ° 4-10 грех 135 °) = 3.47.
Амплитуда косинуса 3-й гармоники = 7 S fp W COSP ‡ х = Р-1 = А (7 COS 45 ° 4-11 cos 90 ° 4-13,5 cos 135 ° 4-15,4 cos 180 ° 4–4–17,4 cos 225 ° 4–20,5 cos 270 ° 4– 25,4 cos 315 ° 4– 4– 32,5 cos 360 ° 4–27,7 cos 45 ° 4–19,2 cos 90 ° 4–10 cos 135 °) = 5,1. Амплитуда первой гармоники ряда Ax = K (AJ) 1 4- (L ‘) 3 = 25,9.
Первое начало угловой касательной первой гармоники IS смещено к началу кривой f (X) T -5,23 25,3 = -0206; ^ = -11 ° амплитуды третьей гармоники A3 40 «= _ | _ (A») 2 = 6;. «Tg ^ = 4 = 1,47; ips = 55 ° 50 ‘. Следовательно, при ограничении третьей гармоникой, ‘/ (о) /) = 25,9 sin (о / -11 ° 40’) + 6 sin (ЗСО / + 55 ° 50 ‘).
На рисунках 217, b показана 1-я и 3-я гармоники результирующего ряда и результирующая (общая) кривая, которую можно сравнить с кривой на рис. 217. Для кривой ряда Фурье f (x) значения этих функций не являются последними, но находятся в середине интервала p, то есть x, по / p (x), sinp ^ x, cospkx в уравнениях (8.5) — (8.7) == pDx, а не x = (p-0.5) Dx.
Смотрите также:

