Определение движения по заданным силам

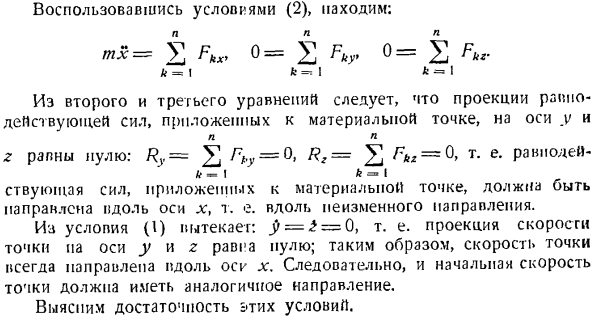
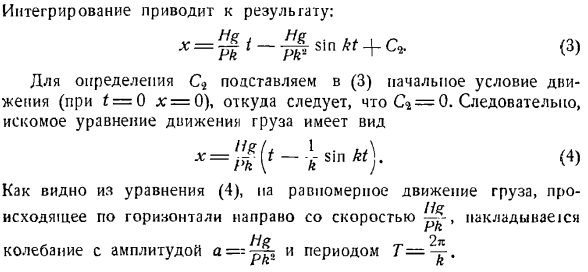
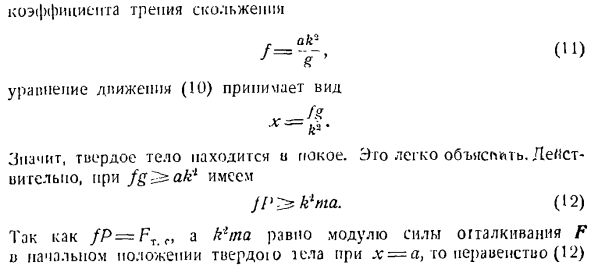
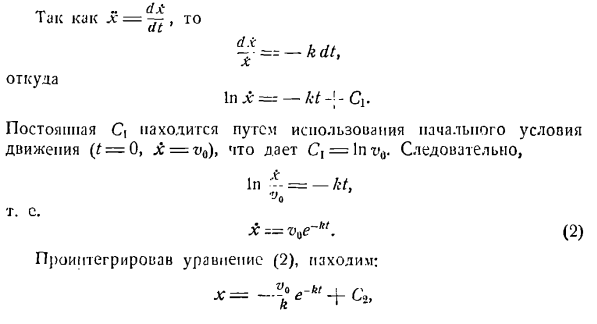
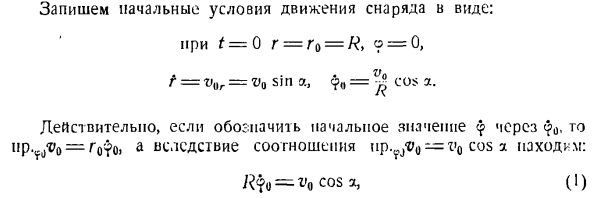
Определение движения по заданным силам

• Определение движения по заданным силам (Обратная задача динамики массовых точек） Сила, приложенная к точке масс M F, F * …, Fn>is given. To определив закон движения этой точки, необходимо закрепить систему дифференциальных уравнений движения, которая соответствует выбранной системе отсчета. Поэтому, если задача также решается проекцией от оси декартовой системы координат, то система дифференциальных уравнений движения подлежит интегрированию. / «- в-в> Ф **> МВ-Гкгm > = в ( я *） к.. Я-1-я А результат интегрирования этой системы определяет закон движения точек в декартовых координатах. Г = М 0> р =

(О- Решение обратной задачи, связанной с интегрированием системы дифференциальных уравнений (I), может быть серьезной проблемой, и в ортогональном случае часто не представляется возможным сделать это самостоятельно. (Тогда вам нужно решить систему численно (1), применить другие методы приближенного интегрирования или использовать компьютер.） Поскольку система (I*) состоит из 3 дифференциальных уравнений 2-го порядка, то при интегрировании вы найдете 6 произвольных констант C|, C, СЛуQ. Q и Q отображаются. Дорожная ситуация. Соотношение(2) является первым интегралом дифференциального уравнения движения(1).

Чтобы определить закон кирпичной кладки, замените Формулу (3) dx х-на. Людмила Фирмаль

чтобы определить интегральную постоянную Cj, подставьте начальное условие движения (i = 0 для x = vy) в Формулу (2), но помните, что C \ =!•<, Будущее. Полученное значение c заменяется выражением (2). .V = v0 g (sin a-J).) Т. (3） Когда вы изолируете переменную, вы видите следующее: (Форекс = VQ вы ьли-Джей — (Син А — / соз а)^ ДТ£.Когда вы интегрируетесь, это выглядит так: х = v0t + \ £(грех а- / соз а) T * — (- с (4） И Интегральная константа C \определяется после подстановки начальных условий, удовлетворяющих формуле (4) (f = 0,η= 0). С = 0.Если ввести это значение Cr и(4), то получим уравнение движения кирпича. х = vQi-Джей — ^(грех-я-/ я)/ * (о） Надеюсь Нуга — (синоу — / соз А) В2. Подставляя число, получаем 5 = 7,02 м. При решении этой задачи,

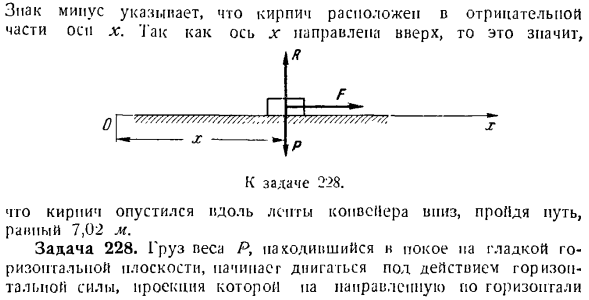
когда ось x направлена вверх вдоль конвейерной ленты, начальным условием движения является следующий вид: для T = 0, π:= 0, х-качеству звука. В дифференциальном уравнении движения знак изменяется: [> -X = — P sin I Ft f, g e. X = — g(sin i — / cos7). б. Повторите решение этой задачи и получите следующее: x = — ^(sin a — / cos a) t 4-C,,, C,= — X’O, x = — \ vQ§(sin i — / cos i） * = — /г»0 / — [- г з {я — / я)[} Дж-Р С * С2-0, х = — J Я — / потерь J、 с = Я-г-г(грех-я — / Кос 7.) ^ Дж, с =-7.02 м Знак минус указывает на то, что кирпич лежит на минусовой стороне естественного po X. Поскольку ось l направлена вверх, это около.

• ;; ////////////。:; Центы./ Р-1-Ф.» П. С. Задача 2Г. Чтобы кирпичи спускались по конвейерному клещу и проходили трассу со скоростью 7,02 м. Задача 228.Груз массой I, который был неподвижен на гладкой горизонтальной плоскости, начинает обходить под действием горизонтальных сил, а его проекция направлена горизонтально Ось x справа-Fx = Hs \ nktt. Где h и K-постоянные величины. Найдите закон движения груза. Решение. Получаем начало координат оси l в исходном положении груза. Запишите начальные условия движения, учитывая, что в первый раз груз был неподвижным. как t-0 x = 0, x = 0. К нагрузке прилагаются следующие силы: P-вес груза, F-

движущая сила, а R-вертикальная реактивная сила горизонтальной плоскости. дифференциальное уравнение движения груза в проекции на ось X、 -х-FC или X-грех И. Г х р Дуплексный. чтобы отделить переменную «= then», это выглядит так: ДХ = грех КТ поделки Откуда? х = — $, потому что КТ + КБ. (1） (1) подставляя начальное условие (/=0 X «= 0) находит HP. когда вы присваиваете значение Ct этому выражению =(1)、 £ х = ’ — » fcoskt.(2） дуплексный. для x—■ — разделите

Как видно из уравнения (4), при равномерном движении груза, идем вправо горизонтально со скоростью. _ Качания амплитудой A и периодом 2л Людмила Фирмаль

переменные в выражении (2). ДХ = ДТ-й кос ДТ м. Интеграция дает вам результаты. х = м {—J в $ Си «т + с * <3> Определить, подставив начальные условия движения (t = 0 l:= 0) в (3), C * = 0.So, уравнение движения груза принимает вид: Х = «£[Т-Я-Грех(4）

Внимательно рассмотрев решение этой задачи, можно увидеть, что равномерное линейное движение груза является следствием начальных условий соответствующего движения (наличия В Формуле (2) постоянного члена Начальное условие миграции, при котором нагрузка только колеблется. Для этого константа интегрирования C {должна быть в уравнении (1)) исчезает. Из уравнения (I) Герц. получаем T = 0 и C,= 0 xQ = — pjr. В результате, если указано в состоянии вопроса, что в первый момент груз будет уведомлен слева、 В случае

по модулю уравнение (2)принимает вид: X = — ^ cos kt、 А уравнение движения груза имеет вид x = — ^ sin kf, respectively. So … Характер движения груза зависит от величины начальной скорости. Поскольку начальное положение груза в этой задаче не было задано, мы выбрали начало координат оси x в начальном положении груза и получили xQ = 0.Выбрав начало координат оси x в другой точке получим x0 f 0 тогда на основе Формулы (3), C2 = .v0, и дополнительные члены x0 включены в уравнение(4).Поэтому от выбора точки отсчета зависят только значения постоянного члена,

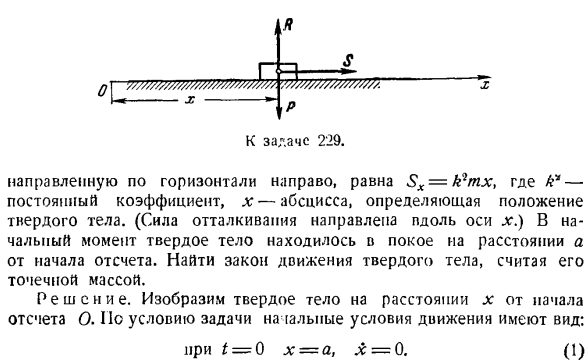
которые не влияют на характер движения груза. Задача 229.сила отталкивания, проецируемая на ось x, применяется к массе M твердых тел, которые могут перемещаться вдоль оси X. К выпуску 229. ЗХ = к ^ МХ. Где K * — постоянный коэффициент, а x-абсцисса, определяющая положение твердого тела. (Сила отталкивания направлена вдоль оси X.) В первый момент твердые тела были неподвижны на расстоянии а от опорной точки. Найти закон движения твердого тела и считать его точечной массой. Решение. Рисует твердое тело на расстоянии x от опорной точки O. В зависимости от рассматриваемых условий начальными условиями выполнения упражнения являются: 0.） При t = 0 x = a, x = 0.

Следующая сила приложена к твердому телу. P-вес груза,# — вертикальная реактивная сила гладкой горизонтальной плоскости, а 5-отталкивающий сплав, идущий из точки O вправо. вид дифференциального уравнения для движения твердого тела в проекции на ось x имеет вид ТХ-ЗХ. Sx = k’1mx.、 .е-kgx=0.(2） Чтобы решить дифференциальное уравнение (2), которое является линейным уравнением 2-го порядка без коэффициентов справа, создайте соответствующее характеристическое уравнение. Х * — Л * =

0、 Откуда? > 4 С 3 = к РЗ. Если окажется, что корень характеристического уравнения является вещественным числом, опишите решение уравнения (1) в виде: х =схема в-J-С ^ Е-бл. (3） Чтобы определить константы интегрирования Cj и C2, нам нужно 2 уравнения. если X является производной по отношению к i, то это выглядит так: х = Cvkekt-с%ке-М (4） Присвойте начальное условие(1)выражениям(3) и (4), а затем、 Если решить полученную систему уравнений, то можно увидеть, что Ci = C2 = ’ J. (3) в CA и C. подставляя значение 2 становится желаемым законом движения

твердого тела. икс+ = С помощью гиперболического косинуса угла kt можно также записать: л:= а КФУ КТ. Теперь предположим, что горизонтальная плоскость не является гладкой. Если коэффициент трения скольжения равен/, рассмотрим влияние силы трения скольжения на движение твердого тела. Силы, приложенные к твердым телам P, S и H, добавляют силу трения скольжения Fr c = / P, которая направлена в противоположном направлении к движению, то есть влево в горизонтальном направлении. При Эюм футов вводи

т в правой части дифференциального уравнения движения со знаком минус. Дифференциальное уравнение(2)принимает вид: Х-КЛК = —ФГ. (6） (5） Общее решение неоднородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами x равно сумме общих решений x{соответствует однородному уравнению, а частное решение формулы x * 4 равно правой части, то есть левой стороне. = — ; -.V. 2. (?） Общее решение xt задается формулой(3).Рассмотрим, что правая часть уравнения (6) является константой, то есть ищем конкретное решение в виде xi-L. если подставить это значение в уравнение (6), то d’.2 = A=: «^ Итак, согласно формуле (7), мы видим общее решение х = Cxckt-ру * РКТ-(я）

Чтобы определить константы итерации C и C, выполните следующие вычисления: x = Clkcht-Ciltc — » 1.(9） Получается путем подстановки начального*условия (8) и (9) (1) 1•/ <л Система уравнений, C | = C4 =-.) Д— .Для приведения признаков C, и уравнение (8) C\, чтобы получить искомое уравнение движения твердого тела. Сравнивая уравнения (10) и (р), если существует сила трения скольжения, то движение тела является / ФА. Он будет медленнее. В самом деле, коэффициент(К-а ->, ЦКТ-7е-к \Нью-Джерси меньше, чем соответствующий коэффициент. когда a — = 0, то есть

Начальные условия движения материальной точки определяют положение и скорость точки, а также определенное время. Положение точки определяется 3 координатами x, y, r, а скорость точки определяется 3 проекциями скорости l \ Yi. Следовательно, начальное условие ИД. Форт = т0 х =xφy = г ^ з = н (пятно), х = а «0, то J’ = Д(спот скорость). (Во многих случаях эти условия задаются начальными моментами премии/ = 0.） Начальные условия движения n ncpnv-результат замены 2-го интеграла системы (I551) на ie,

образуется система тестовых уравнений, определяющая 6 несуществующих C, C, C. Материальное движение!, Если на плоскости возникает точка, то определяются координаты x и y и положение плоскости, число Поэтому твердое тело неподвижно. Это легко сделать explain. In факт, fg ^ ak1 имеет JPT по&хна. (12） fP = Frc, а так как bLpa равно модулю силы отталкивания F и начальному положению твердого тела при x = a,

то неравенство(12） Коэффициент трения скольжения Уравнение движения (10) форма Это указывает на то, что модуль упругости силы отталкивания меньше модуля силы трения скольжения. Таким образом, сила отталкивания не может нарушить покоя твердого тела. (Предполагается, что коэффициент ползучести скольжения при движении равен коэффициенту трения скольжения в состоянии покоя.） Задача 230.Прикрепите груз р к правому концу пружины, а левый ее конец к step. At в первый момент пружина не деформировалась и начальная скорость v0t сообщалась грузу, лежащему на горизонтальной плоскости Р. Идти на задание 230. По горизонтали направо. ось x ориентирована горизонтально вправо

вдоль оси пружины, а начало координат находится на правой стороне недеформированной пружины. Если проекция силы упругости пружины равна Fx = — xx-fbf, найти максимальное перемешивание нагрузки. Где x-растяжение пружины, а r и p-положительные коэффициенты константы. Силой скольжения груза по горизонтальной плоскости и массой пружины пренебрегают. Решение. Опишите начальные условия движения груза. если t = 0 x = 0, x = vQ. показывает нагрузку для того чтобы двинуть пока двигающ справедливо вдоль x-axis. In делая это, растяните пружину до x. сила пружины F направлена горизонтально влево. проекция на ось x равна Fx = — = — (*x К нагрузке прилагаются следующие силы: Р-масса

груза, R-вертикальная реактивная сила горизонтальной плоскости, F-сила упругости пружины. создайте дифференциальное уравнение для движения груза, спроецированного на ось X. — (1） Это 2-градусное нелинейное дифференциальное уравнение. Интеграл уравнения ([) для определения уравнения движения груза? И x = f (t)связано с вычислительными difficulties. At в то же время、 Максимальное смешивание легко осуществить. Это связано с тем, что достаточно найти зависимость между x и x и определить желаемое значение,

приравняв нагрузку к x в крайнем случае position. To для этого умножим левую и правую части дифференциального уравнения (1) на dx, учитывая, что Jc dx dx = xdx、 £Х DX =- (ах-Ф-px3) dх. £ Если мы интегрируем это уравнение, мы видим, что: Р * * _ ax2 исправить ’г—2 В первую минуту, η= 0 и= = по качеству звука. Так, П Где уравнение (2) принимает вид: П  / > _ «я _ {$ л» ч л. (Формула(3) может быть

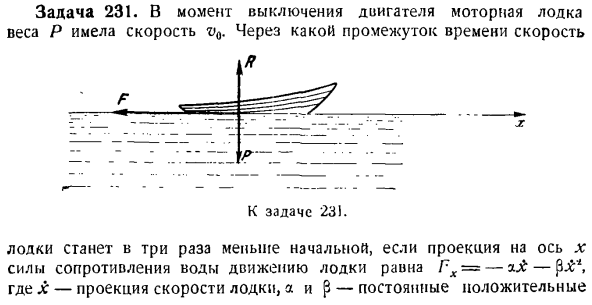
достигнута непосредственно через теорему об изменении кинетической энергии точек материи. См. главу IX,§b ниже.） Момент, соответствующий максимальной смеси а, скорость движения груза будет равна bullet. So подставим его в Формулу(3).х= а, Х = 0.Получить Би-квадратное уравнение для нужного смещения. Если мы решим это уравнение, то увидим, что: а(Вив + ИПГ ^ вл-г). Задача 231.At в момент остановки двигателя, в моторной лодке была скорость весом П. Если проекция на ось X сопротивления воды движению лодки равна Tx = — sufr — {}, то лодка будет находиться первые 3 раза. Количество. ось X направлена горизонтально вправо в направлении

движения лодки. Также рассчитайте путь, пройденный лодкой за этот период. Сделайте лодку точечной массой. Решение. Принимает начало координат оси x в исходном положении лодки. Начальными условиями движения лодки являются: Т = 0 х = 0, х = качеству звука. Позвольте мне объяснить силу, приложенную к лодке: P-вес лодки, R-общая вертикальная сила реакции воды, F-общая сила сопротивления движению лодки в противоположном направлении, то есть

горизонтально влево. создайте дифференциальное уравнение для движения лодки в проекции на ось X. ТХ = FX с \ Поскольку гипотеза Fx = — ax-то CLf-RL(1） Если вы замените x в выражении (1) и затем разделите переменные, это выглядит так: Так… (Форекс =- ДТ(2） Интегрируем дифференциальное уравнение (2) и рассмотрим его 1 = 1___ Х(в ал «(а + ФТФ）» У нас есть：

«В-4-г = -/ −1- С. (3） га а-rpjt 1 ^ ’ При использовании начального условия упражнения (/=0 D ’= x ^ o) в Формуле (3)、 С =—п 1н га а•| » pvQ * Итак, формула(3) принимает вид: (а-| в Формула(4) определяет зависимость между проекцией скорости лодки x и временем t. (4)после замены I = T, x = Определите нужный временной интервал G. тогда скорость лодки будет в 3 раза больше начальной. t_R, З — / — Р»Л На 7-дюймовом временном интервале лодка возвращается к дифференциальному уравнению (5), чтобы определить пройденный путь. D х Это па ДКС. в случае x dx-dx = Jc dx, после разделения Так…

Пояс мы получаем： П Д. Т. — гггг = — ДХ. £ «- ’ОО Когда вы интегрируете это уравнение, оно выглядит так: П. С. В («J-?。= С. (5） С. С. Первый момент= 0 и. Итак, V = Т\, В(В $ по качеству звука). Подставляя значение C в Формулу (o), получаем: П а л ч; л Для определения искомой траектории 5 лодка переместилась от начального момента к моменту, соответствующему начальной скорости vQ 3-кратного уменьшения, необходимо подставить формулу (6). х = с х =тогда — ги в Ф(ЯТ / 0 интересно отметить, что при удельном сопротивлении di-jii лодка не останавливается. Действительно, если вы присваиваете x = 0 и =выражению(4), Вы получаете m = oo. Ограничение

соответствующего пути, пройденного лодкой, может быть определено из формулы (6).Если путь перемещается, s = Iim. в. И Г с И тогда Jim x ^ = 0 и узнайте ниже. т.- Задача 232.Измерение глубины реки осуществляется с помощью троса-опускаемого груза на дно реки. если вы опускаете груз со скоростью r> 0, кабель обрывается и груз достигает дна через G секунд с момента обрыва кабеля. // Проекция на ось x сопротивления воды движению груза Rx = — kmx, где m-масса груза, а x-проекция скорости на ось Xy, где k-постоянный коэффициент. ось x расположена вертикально вниз. Сила

выталкивания груза из воды игнорируется. Решение. Возьмем точку отсчета O в месте расположения нагрузки, которая соответствует моменту отключения. К грузу прилагаются следующие силы: Р-вес груза, Р-сила сопротивления воды движению груза、 Он направлен в противоположную от движения сторону, то есть вертикально вверх. создайте дифференциальное уравнение для движения груза, спроецированного на ось X. Но… МХ = Р + ГХ. (1） Потому что это Rx = — kmx、 Дж = г-КХ. (5） — С. Это дифференциальное уравнение движения груза, которое должно быть интегральным в 2 раза и определять путь, по которому будет двигаться груз. Замена и отделение X от^Формулы(2) после ДТ. — =Второзаконие. Интегрировать GK. * (3

） нет. Пояс, мы имеем： Мы это выясним： — A В (* -«)= * + Q. Перейдите к выпуску 232. Подставляя интегральную константу C (, Формула (3) t = 0 и t = va、 C] = -A в (g-kv0) получается. Если мы введем значение этого Q в Формулу(3), то увидим, что: Так как дифференциальное уравнение движения равно 2, то число начальных условий движения равно 4. С TQ. x = x0, y = \ ’ a (положение точки), x = x0, y = j’o(скорость точки） (В этом случае 2.0 = i (l=: 0). Если материальная точка движется по прямой, то на оси x вдоль пути движения точки существует 1 дифференциальное уравнение движения, поэтому число начальных условий движения равно 2. С TQ. x = xQ (положение точки), x-xQ (скорость точки). Сила, приложенная к точке масс, равна: 1) постоянная сила (например, сила тяжести, когда материальная точка движется вблизи поверхности Земли）; 2) зависящие от времени силы (например, периодически

меняющиеся силы, вызывающие колебания в точках материи）; 3) Сила, соответствующая положению точки (например, сила притяжения и отталкивания, сила упругости пружины, например упругая нить). 4) сила, зависящая от скорости движения точки(например, сопротивление движению точки). Чаще всего сила является функцией времени, положения, скорости и ускорения точки. Система уравнений(1*) имеет вид: МХ=} (т \ х, г, р,.В, Г, Я, у, Z)г Л’ГК. * Откуда? (4） Формула (3), устанавливающая временную зависимость

проекции скорости груза, является первым интегралом производной. ГУ. запрос. Загрузите уравнение движения. Если вы замените X pa в выражении (4) и разделите переменную на oi, это будет выглядеть так: к р После интеграции： ’З’ — кво 0-КТ Ф Р 1 — — — е-т- Х-ки Если присвоить формуле (5) ^ = = 0 и x = 0, то получится C * = _-g ty^.Если вы присваиваете значение C2 выражению(5)、 Способ передачи груза ： (6） Чтобы определить путь, по которому груз проехал за 7 часов

до дна реки, необходимо подставить t = 7, x — //в формулу(6). в результате、 I = = / 7 — ^(1 Задача 233.Парашютист при раскрытии парашюта шел вертикально вниз со скоростью<vQ. Найти уравнение движения небесных сил опер, если проекция на ось x сопротивления движению равна Rx=.Где m-масса десантника, x-проекция на ось x скорости, а k1-постоянный коэффициент. ось x расположена вертикально вниз. Движение пустого троллейбуса рассматривается как движение м.

Т = 0 Л = 0,% = по качеству звука Рисует материальную точку, но время в пути на расстоянии x от исходного положения. Вес^ К задаче 233 прилагается следующая сила: Р — масса его тела, # — общая сила сопротивления движению, направление, противоположное движению, то есть вертикально вверх. создайте дифференциальное уравнение для движения проекции по оси X. н. Потому что Rx = — fP / nx *、 Х =(1） Это дифференциальное уравнение движения. если

вы пишете x =и разделяете переменные в выражении (I), вы можете видеть, что: dt. д. т. н. — Второзаконие. (2） Интегрируем уравнение (2) и рассмотрим его  / ’、 J ^ С-К * Л * 2 г’g \ у’g-Ф-К * 1 г’g-КЛ-Джей Мы получаем： Я «= 2бв-ГТ-\ — С,.(3） Подставляя начальные условия в уравнение(3), получим C,= In-if (£=0 jc= T / rt>.Выражение(3)принимает вид） G-liVQ = ЮИД. если вы решите это уравнение для x, оно выглядит так: Е2 к(ВК \ kv0)!Т V * ’+(г г-kv0)’ Или = VII(С С ’ ^ + 1） — К. Чтобы интегрировать уравнение(4), Замените

x на〜и разделите переменные. В связи с тем, что правая часть уравнения (4) является громоздкой и трудной для интегрирования, можно записать уравнение (4) в гиперболическую функцию, используя следующую формулу: e12 + 1 = 2c2 ch g, c12-1 = c2eg sli g. Формула(4) принимает вид: = = Против yyyyk жира) — \ — kv0ch(к yjt)(5） к г. ч(МПТ футов)+ kv0 ш(’gt Фе V) 1 Откуда? ДХ = = ва’g в * ч <к V&)+ кВ «ч V и) ДТ (0） к ви(Е ^ О + ш(а)/£/） Нетрудно заметить, что числитель правой части уравнения (Р) является производной или

знаменателем дроби дроби. kyg. So, это выглядит так: * = Находится в \ Vg ch (k Y’gt)+ Ave sh (k V’GL)] + C4. (7） Если подставить начальное условие в формулу (7) (Если t = 0 lr = 0), то увидим, что C2 =-p 1n yg. Подставляя значение этого Q в уравнение(7), получаем уравнение движения, необходимое для пустого параболического пространства. * = 1 м [ч(К, Г ’ ГТ)+ пр сли(/ г / — ГТ)]. (8） Определим величину, которой подвержена скорость парашютиста, который будет стремиться к длительному спуску с большой высоты. То есть мы вычисляем предел x в t — > co. To для этого воспользуйтесь формулой (5).Если разделить числитель и знаменатель справа на ch (ky gt), то получим:

ВА В » Е-ІВ(к ВГТ) — kv0 К \ г-ч kv0•й {К Г ’ ГТ) ’ учитывая, что Lim Е (К в ГТ)= я、 / — ОО Обод. / — КО К То есть, когда спуск будет длительным, движение войск небесного трона будет приближаться к равномерному со скоростью, не зависящей от начальных условий движения. Задача 234.Вертикальная ось пустого троса происходит без начальной скорости/ / с высоты, при наличии силы сопротивления, указанной в условиях предыдущей задачи. Определите скорость движения парашютиста в момент приземления. The solution.

To определив скорость движения парашютиста при приземлении, нецелесообразно повторять решение предыдущей задачи. Потому что при интегрировании во времени проекция скорости x и координаты x находится в виде времени function. It необходимо определить время 7 \, соответствующее высоте нисходящего па//из уравнения движения, а затем подставить полученное значение T в x для определения

требуемой скорости. В этой задаче удобнее получить x по x, то есть выразить проекцию скорости парашютиста по положению x парашютиста, подставив x = Iy для определения искомой скорости V. Для определения зависимости x = f (x) необходимо применить методику умножения левой и правой частей дифференциального уравнения движения на rfx. Это приводит к немедленным результатам и интегрирует дифференциальные уравнения движения

Происходит только 1 раз (в предыдущей задаче для определения закона движения x = f (t) мы выполнили Интеграл 2 раза). Чтобы применить описанную выше методику, опишите дифференциальное уравнение (1), полученное при решении предыдущей задачи в виде: xdx =(г-к***) ДХ. (Я） Учитывая, что J? если разделить dx =〜dx = x dx и переменные в уравнении (1), то получим: xdJt г = р * = ДХ- Если мы интегрируем это уравнение, мы видим, что: −2£2 1 n(•?- =Х «* РК-(2） В случае начального положения пустого блока ТРО, то есть x-Q, его скорость согласно рассматриваемым условиям была равна нулю, то есть x = 0.Когда мы присваиваем эти значения Формуле(2)、 с — = — Ык * Если подставить полученное значение C,

то выражение(2)примет вид: Дж. ч = х 2 к * г-к * Ят * * где ты? Формула (3) определяет прогноз скорости парашютиста в зависимости от положения парашютиста. Чтобы найти скорость десантника при посадке, нужно подставить Формулу (3): x = I,£= v. и далее… в = л-ВГ(1 Как указано, Вы можете получить тот же результат, но более трудоемким способом, используя формулу, полученную при решении предыдущего problem. In в самом деле, запишите формулы (o) и (8), полученные в предыдущей задаче, и установите для них^ 0 = 0. Ят = ^ — ТБ(кв ГТ). (4） * = ilnch (/г ГТ). (5）

Из Формулы (5) укажите длительность спуска десантника с высоты с помощью Γ, тогда она выглядит так: ч (с V <РТ)= ЭК°Н. т он, Си » т \ г ТТ | 4 (К Г Г Т) −1 е (kygT)= — с ч(к ВГТ） ту (к VrgT)= = вл И затем… (6） Искомая скорость определяется по формуле (4) и устанавливается равной t=. T, x = V. используя формулу(6), можно увидеть следующее: в =±ВГ（- Задача 235.Камень брошен вертикально вверх со скоростью зв. Если проекция на ось x сопротивления движению R равна следующей, то определяют, насколько высока скорость движения камня на половине высоты H от поверхности Земли. На оси X скорости существует постоянный коэффициент. ось

x направлена вертикально вверх. Решение. Возьмите точку отсчета на оси x земной поверхности в исходном положении камня. 2К * ч Начальными условиями для движения являются: 0.） если t = 0, X = 0, X = = ■Vq. Вес камня выражается в R. следующая сила прилагается к камню. P-его вес, R-сопротивление движению, противоположное направлению движения, т. е. перпендикулярное П. С. Р. икс jl ту МЗ Вы можете решить проблемы, используя материальные проблемы и ключевые моменты решения. Смотрите следующую последовательность: 1) » Выберите систему координат. 2) Запишите начальные условия движения точек. 3) на рисунке показана заранее установленная сила и сила реакции связи, приложенная к материальной точке. 4) Создайте дифференциальное уравнение для движения точки масс. 5) интегрируйте систему дифференциальных

уравнений движения. Используйте начальные условия движения для определения константы интегрирования. Вниз. создайте дифференциальное уравнение для движения камня, спроецированного на ось xi ^ jwJ?=- Р ’+ РЖ О. ГХ = — klmx \ тогда (2) к выпуску 235. Необходимо определить местоположение камня по скорости, в зависимости от ситуации в question. So, применим методику, использованную в предыдущей задаче, то есть левую и правую части дифференциального уравнения (2). умножить на DX： если xdx = xdx и вы разделяете переменные, перепишите уравнение (3) как: Если

мы интегрируем это уравнение, мы видим, что: — =(4） Используя упражнение лоскутное условие(1), Вы получаете следующее: (г + кВт). Если подставить это значение в Формулу(4), то найдем: * ’1П |±С. (О） 2к1 г + к-Х2 * ’ Уравнение (о)выражает связь между расположением камня-i и его velocity. To определить высоту и подъем камня, соответствующие уменьшению начальной скорости vQ наполовину, необходимо: Подставим x = I, I = Then в формулу(5) Задача 236.Определите условия. Это обеспечивает перемещение материальных точек в плоскости. Решение. Поместите оси x и y в плоскости, где расположена траектория точки масс. Тогда r = 0 и оттуда И > ’=0.(2） Описывается система дифференциальных

уравнений для движения массовой точки в проекции на ось декартовой системы координат. С. С. С. МХ =£Gkx> ту =£fky по> МЗ =£ФКР к-1 к =)к-1 Используя условие(2), можно увидеть следующее: МХ = Gkx в МУ = X Ф * в° = £ к-я к)к = 1 Из последнего уравнения мы видим, что проекция на ось z результирующей силы, приложенной к точке массы, равна нулю. н. ^ Fkz = 0, то есть результат находится в плоскости、 k = I Куда перемещаются точки. Условие (1)= =(из J проекция скорости точки на ось z равна нулю, то есть скорость

точки находится на плоскости, в которой движется точка, следовательно, начальная скорость точки находится на той же плоскости. е. Изучите достаточность этих conditions. At первая точка, предположим, что точка находится в плоскости xy, то есть r0 = 0, и начальная скорость точки находится в той же плоскости, то есть£fl = 0, и результат силы, приложенной к материальной точке, находится в той же плоскости. н. Другими словами,/?, = £ФКЗ = 0. ч-1. Если эти условия выполняются, достаточно ли этого для движения точки массы в плоскости xy? Дифференциальное уравнение движения

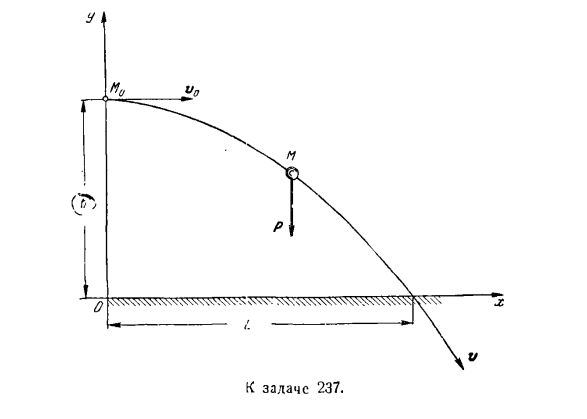
важной точки в этом случае принимает вид: н МХ =£Gkx, му = х Fby> МЗ = 0 —1 Из последнего дифференциального уравнения находим i = C. Поскольку i0 = O, Ci = 0, а следовательно, и 2 = 0.Тогда z = C. Но поскольку это^, 1 = 0, C * = 0, а следовательно, z-Q. из полученных результатов z = 0 указывает, что движение точки массы происходит в плоскости xy. Поэтому движение материальной точки в плоскости требует и достаточно того, чтобы начальная скорость точки и результирующая сила, приложенная к этой точке, находились в одной плоскости. Задача 237.С поверхности Земли человек бросает камень из точки На высоте h, сигнализируя о горизонтальной начальной скорости r»0.It решает!»Уравнение траектории, дально

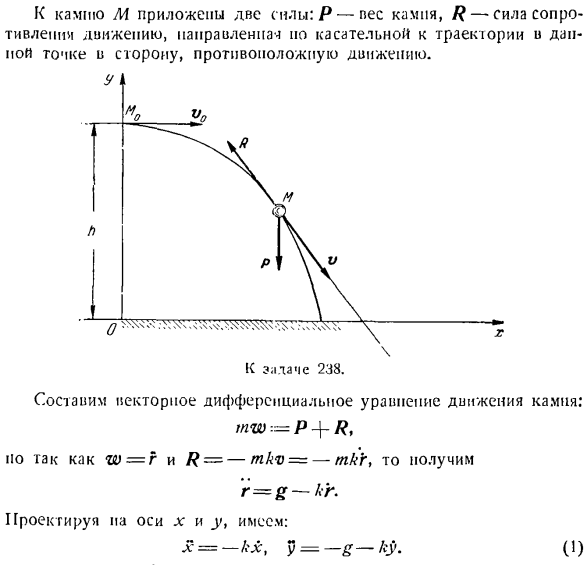
сти полета и скорости камня в момент его падения на Землю. Сопротивление движению и искривлению земли игнорируется. Решение. Выбранная система декартовой системы координат показана на рисунке. А10-начальное положение камня. Давайте нарисуем камень, двигаясь в среднем положении M. указывает вес камня R. добавьте только 1 силу к камню. Вес равен P, но перпендикулярно вниз. Потому что начальная скорость r / 0 и сила P находятся на вертикальной плоскости xy、

Поэтому достаточно создать 2 дифференциальных уравнения движения в проекции на оси x и Y. Напишите начальные условия движения камней： если f = 0 x = 0, y = ft, x = vQ, y = 0. (Во многих случаях при решении таких задач они случайно прикладывают определенную динамику к материальной точке, но в заданной точке по направлению движения они поворачиваются по касательной

к траектории. Начальная скорость V0 является результатом удара, происходящего в течение очень короткого времени, равного 1000 минутам 1 секунде. Для начала отсчета времени возьмем момент окончания удара, когда камень приобрел скорость f0.Эту инструкцию следует учитывать при решении задач с полетом пуль, снарядов и т. д. Поэтому давление порохового газа на пулю или снаряд появляется, когда он передает начальную скорость. дифференциальное уравнение движения камня в проекции на оси x и Y. Техас:= 0, ту = — Р、 Или x = 0, p = — g. Если мы интегрируем

дифференциальное уравнение= = 0, оно выглядит так:* = for = = 0 x = vQf, поэтому Ci = zv, следовательно, в любой момент времени ± = в = прибл. (Я） если написать x =〜и затем интегрировать уравнение (1), то получится: х = vQt — {- СЧ. (2） Так как момент t = 0 x = 0, то из Формулы (2) следует C9 = 0.So, выражение (2) можно, наконец, записать в виде: х = вю. (3） Для интегрирования дифференциального уравнения p z = — g замените J7 на dJf. Когда вы изолируете переменную, вы видите следующее: ды =—ГДТ. Итак, если мы интегрируем это уравнение、 J = — gt + C2. (4） поскольку t = 0 y = 0, уравнение(4) для C3 = 0 и уравнение(4)принимает вид: )- =- &- (5）

Выполните последующее интегрирование, сначала заменив j>на^и разделив переменные. И затем… +(си） поскольку t = 0 y = h, C4 = = / i, а выражение(6)принимает вид: г =(7） Уравнения x = v9t, (3） г =(7） Определите законы движения камня. Исключите время из этой системы, чтобы найти уравнение орбиты камня. Траектория представляет собой параболу г = н — £іх’ — (с） Так… 6)определить искомое значение, используя траекторию движения критических точек, полученную в предыдущем пункте. При составлении дифференциальных уравнений движения необходимо учитывать массу точки текущего местоположения. Для перемещения свободных материальных точек удобно использовать систему осей в декартовых координатах. Криволинейное движение несвободных материальных

точек позволяет легко решать задачи в проекции естественной трехосности ила. Если йод смещается под действием центральной точки F, то удобно использовать дифференциальное уравнение полярного координатного движения или формулу вине. = __ Р-Ф диджей * \ г} 1 г 4tC * г (§ 2). Задача 226.Определите условия. Как только это условие выполняется, важные точки перемещаются линейно. Решение. Направим ось x вдоль прямой траектории точки масс. Если двигаться вдоль этой оси, Y = 0.Следовательно、 j)= i = 0(

1) J} = 2 =0.(2） Напишите дифференциальное уравнение системы движения в проекции на ось покойного координаты： МХ =FBX в£, М $ = Г] Fby МС = £ФКЗ. k■= I k = 1 k-I Дальность полета камня определяется нарывами при его падении на Землю. Подставим уравнение (8)_y = 0 для определения дальности полета. Чтобы найти скорость камня при падении, используйте формулы (I) и (5) проекции скорости на ось декартовых координат. — Х = качеству звука,(1） Год>*•(&—）

Учитывая, что момент времени Г, соответствующий падению камня на Землю, равен t = T y = 0, вычисляется по формуле(7). Т-МКФ. В результате прогноз скорости падения камней дается по формуле： Далее, коэффициент скорости ВМ〜+ Яф = ВВ \ — Р Косинус направляющей скорости имеет следующий вид: Потому что(XyVf) -=, потому что(г, ДФ)=-1 / .2fh) НХ. в ВТ ыв * _J. 2г / я Вт VЩ+ 2gh 2 силы приложены к камню M: P-вес камня, R-сопротивление движению и、 Цель 238. Создайте векторные дифференциальные уравнения для движения камней. МВт-П +Р. ш= R и R-мкВ = — tnkr、 если

вы проецируете его на оси x и y, он выглядит следующим образом: х = — / СХ, П = — ^ Т—(1） —(У Тиик как X = — тогда ДТ ’ Откуда? 1ш = — л / Ди- Константа C получается при использовании начальных условий{t = 0,^ =для упражнения. Это дает Ci = 1 n r’0.So … В — == — / г /、 т. к. (2） Если мы интегрируем уравнение (2), то найдем, что: + с 、 И если t = 0 x = 0, то = So、 Чтобы решить 2-е дифференциальное уравнение(1), Замените dv Y равно£, и переменная разделяется. =

Второзаконие. по мне-Г И затем… — J = ^ + Используя начальные условия упражнения (=0 j ’= 0), можно увидеть, что C3 = — ^ In G. So … Откуда? Заменяя уравнение (4) pa-и интегрируя это уравнение, оно выглядит так: В = — и-т-с футов 1 фут- * 1 Т = 0, г = ч, С4 = ч — (-, следовательно,、

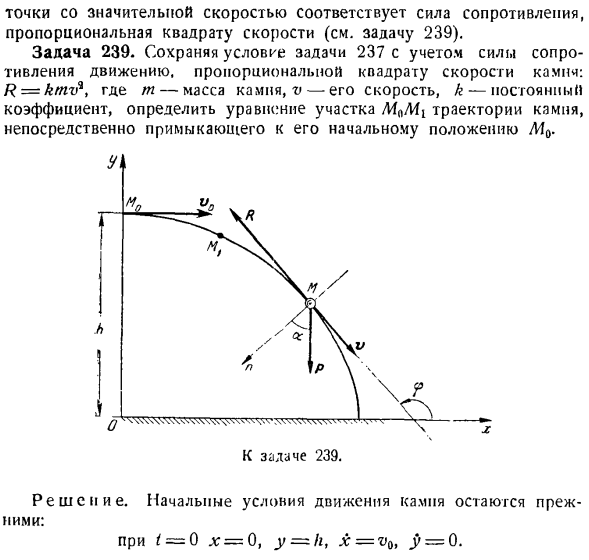
Поэтому камень движется по следующему уравнению: х = *(- е’), (3） г = ч-е-т + л (- с- «).(5） Определите уравнение траектории движения камня, исключив время из системы(3) и(5). / Г8 версии v0-КХ Р ква При движении с малой скоростью сила сопротивления пропорциональна 1 степени скорости точки. Материальное движение Точка с критической скоростью соответствует сопротивлению, пропорциональному мощности 2 (см. выпуск 239). 2.Исходное положение У0. Сделать Ф в /■ В. / ч. 1 ^ hhhhhhhh ХХ * / ’Н YVi / П \ \ П \ Д1 \? Задача 239. Решение. Начальные условия движения камней остаются прежними. Т-0 х = 0, у = фр х = качеству звука и j> =

0 Направление сил P и R не изменилось по сравнению с предыдущим task. So … / ? =- КМВ = — ktnvr. Напишите векторное дифференциальное уравнение для движения камня： МВт = Р-Ф — Р Или ？ = г-КВР. Если спроецировать его на оси, вы получите у. х = — з、{[） В = — г-БВС>. (2） Для интегрирования дифференциальных уравнений (I)、 (ІХ ДЗ x на A v pa d(где c — координаты дуги, измеренные вдоль траектории от точки. После разделения переменных это выглядит так: Откуда? III

и х = — / га — • — ы.(3） При начальном положении камня, то есть a = 0, скорость X = проекция vn. So, C = 1nr> 0.Если мы присвоим значение этого C Формуле(3), то найдем, что: — Л = — в、 Иначе говоря (1） Для упрощения решения задачи вместо дифференциального уравнения (2) Используем дифференциальное уравнение движения камня в проекции по основному закону N. н. т—= р, потому что Р (Сопротивление R дает снарядам проекцию на главный закон, равную пуле). a = 2m — f°=£°= 2 k = I fc = * I L:= 1 Из 2-го и 3-го уравнений следует проекция равнодействующих сил, приложенных

к материальной точке y и н z равно нулю: Ry = ^ Ft. y = = 0t Rz = ^ Fbz = 0, то есть к-я к я Силы, действующие на точку масс, должны быть направлены вдоль оси Х, то есть в одном и том же направлении. Из условия (I) это выглядит так: j> =£= 0, то есть проекция скорости точек на оси y и z равна пуле. Поэтому скорость точек всегда направлена вдоль jc-axis. As в результате начальная скорость точек будет в аналогичном направлении. Давайте рассмотрим достаточность спокойных условий. Если подставить полученное

значение в формулу(6), то получим: 1 л. К. P’o \ — y’l*) l <>(1 L-’ Иначе говоря г = — J в ^ сов ’ в(7） Используя формулу (7), перепишите формулу (5)в форму: учитывая ^ vl cos — = — vzosy = x}и Формулу(4), это выглядит так: (8） ДХ ОИ 1; В связи с условиями задачи необходимо определить уравнение плоской части орбиты A1LM, непосредственно примыкающей к исходному положению точки A10.Поскольку эта часть локуса близка к горизонтальной, мы можем комплексно заменить уравнение (8) a на x (разность g-c-величина 2-го порядка

Малая) вплоть до 1-го порядка малого члена, принимая во внимание значение 1-го порядка малое. Дифференциальное уравнение(8)принимает вид: Это приближенное дифференциальное уравнение интегрируется. к<«- 」 если x = 0 ^ = 0(касательная траектории в точке A / n является горизонтальной).Когда вы присваиваете эти начальные условия выражению(10), C / следовательно, выражение(10)принимает вид: фирма DJL-а _ ЭК-кх(я） Интегрируя дифференциальное уравнение(11), получаем: в =—!-

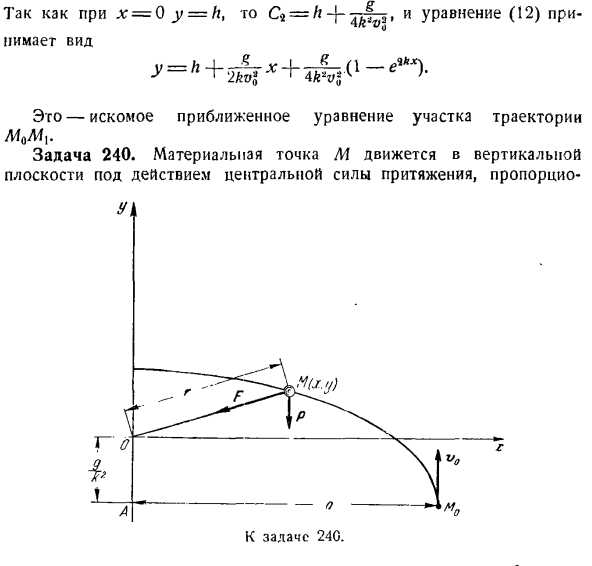
Компания. (12） для η= 0, y = h, C4 = /-|—3 ′ и Формула(12） 4 / с вентиляционно-перфузионное Это выглядит так Дж 1 икв%1 ′ Это и есть искомое приближение отрезка пути. Задача 240.Точка массы M движется пропорционально в вертикальной плоскости под действием Центрального притяжения.

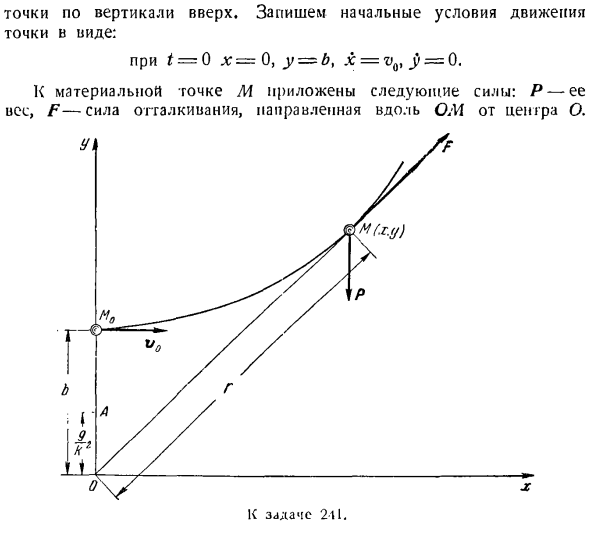
Фиксированное расстояние до центра: F = — k * / nr, где r-радиус вектора точки,//?- Его масса, N-постоянный коэффициент. Найти уравнение траектории движения точки, если в первый раз занято положение M0, а скорость©0 была указана Вертикально вверх (см. Фото). Решение. Начало координат оси в декартовых координатах получается в фиксированном центре O, где притягивается L1. ось Х проходит горизонтально вправо, а ось Y-вертикально вверх. Опишит

е начальные условия движения точек в виде: если t = 0, то x = a, y = -^, x = 0, j)= Vq. К материальной точке М приложена следующая сила: I-сила притяжения, направленная к неподвижному центру ее веса, F-О. Создание векторного дифференциального уравнения движения материальной точки МВт = п — \ — ф Или Р = г — г#. При проецировании на оси jc и y это выглядит следующим образом: Х + к-Х = оть(1） Г-т-к * г = — г. Уравнение(1)является однородным линейным дифференциальным уравнением с постоянным коэффициентом 2 order. To интегрируем, создаем характеристическое уравнение X *

— j-k * = 0, ’ откуда X] 2 =’ Jzki. So, общее решение дифференциальных уравнений (I) можно записать следующим образом: Х = С, потому что КТ-Ф kty С2 грех(3） Где C и C * — константы интегрирования. Чтобы определить Q и C, вычислите х = — Cxk грех КТ-Ф-ЦИК, потому что КТ(4） Затем подставим Формулу (3) t-0, x-a и Формулу (4) t = 0, x-0.С,= а, с \ = 0.Эти значения C и C \в Формуле(3) выглядят так: х = соѕ КТ. (о） В отличие от дифференциального уравнения(1), дифференциальное уравнение (2) имеет вид inhomogeneous. As в результате его общее решение имеет следующий вид В〜В1 + Уу(6） Где y ). C2coskt-F

в Qsin(10) Чтобы определить константы интегрирования Сл и с, вычислите: =- С,* грех-Т-Л-дь, потому что(11） Затем подставим f =()в уравнение (10), у= — и в уравнение (11)= = 0, j> =затем подставим значения C » = 0,=Эти C, и в уравнение (10) С\получим： г = В * — л. (12） Итак, уравнение движения точки массы имеет вид: = салат ромэн Чтобы определить уравнение орбиты, необходимо исключить время из уравнения движения. Я заметила. потому что Сина=; — {,+£）、 Получаем искомое орбитальное уравнение (ТРВ а! т. ^ / г.,- =У (Eiu-уравнение эллипса, центрированного в точке A (0, — j ^ J).1. одна ось

эллипса равна a, другая ось равна Задача 241.Под действием Центрального отталкивания пропорционально расстоянию до неподвижной точки масса перемещается в перпендикулярной плоскости: F = k ’ 2mry, где r-радиус вектора точки, Mu m-ее масса, а N-постоянный коэффициент. Страница уравнения для траектории движения точки, если в первой точке занимает положение Af0 (OMq-

b) и имеет скорость t»0, направленную горизонтально вправо. Решение. Начало декартовой системы координат получается с фиксированным центром O. или его центр Af отскочит. ось jc проходит горизонтально вправо, а ось y проходит через начальное положение Точки в вертикальном направлении. Опишите начальные условия движения точек в виде: Т = = 0 х = 0, г = ^ Б, х = vQ1 г =0.Следующая сила приложена к точке масс M. P такова Создайте векторное дифференциальное уравнение для движения массовой точки. МВт = р-р Z7 резца、 Или — р = г + к Ир. если вы проецируете

его на оси x и y, он выглядит следующим образом: — =(1) г — = — г. (2） Уравнение(!) Является линейным однородным дифференциальным уравнением, коэффициенты которого являются постоянные 2-го порядка. Чтобы интегрировать его, мы создаем характеристического уравнения Х4-КЛ = 0, whice \ xrl ПО =±я У. таким образом, решение дифференциального уравнения (1) можно записать в виде: х = шек(+ ХГ-б .(3） Дано: в первой точке точка находится на оси x, то есть при y ^ = z ^ — = 0, а начальная скорость точки ориентирована вдоль оси xy.

Yn — = i0 = = O, результат действия силы, приложенной к точке массы, направлен вдоль оси L. н. Нужно ли мне выяснить, достаточно ли этих условий для линейного перемещения точек вдоль оси x? В этом случае дифференциальное уравнение движения важной точки принимает вид: mx = Y] Hbx, mu = 0, mz = 0 и J Из 2-го дифференциального уравнения wp = 0 видно, что j) = C. так как j> 0 = 0, то Cr = 0, следовательно, J> = 0, а y = C. Поскольку _y0 = 0, то Gi = 0, следовательно, y = 0.Аналогично, мы получаем<r = 0 из 3-го дифференциального уравнения. Из результата y = = z = 0 масса движется вдоль оси X. Поэтому для реализации линейного движения материальной точки начальная скорость точки и н.

Чтобы определить константы интегрирования C1 и C9, вычислите х = Qkebt-Cqke-КТ(4） А затем подставим Формулу (3)/ = 0, jc = 0, и Формулу (4) i = Q, x = v0.Тогда мы получим систему уравнений. 0 = КТ + С * версия v0 = С \ К-К МФ. 1) D Решение этой системы приведет к Q = ^и C9=.So, в итоге это выглядит так: х = \ л-е-т)= ^°ш КТ. (5） Поскольку дифференциальное уравнение (2)неоднородно, его общее решение y имеет вид: Y-Y \ + Y *(6） Где Y-общее решение соответствующего однородного уравнения. г-к * г = 0(7） Уч представляет собой конкретное решение Формулы (2). Поскольку дифференциальные

уравнения (1) и (7) аналогичны、 Y r = C3-f(8） Правая часть дифференциального уравнения (2) имеет вид constant. So, находим конкретное решение в виде константы: y * =A. Если положить yq = A в Формулу(2), то оно должно выглядеть так: Л =(9） Используйте формулы (8) и (9) для описания общего решения в формуле (0). Г = +(10） Чтобы определить константы интегрирования C3 и C4, выполните следующие вычисления: год.-= С ^ kekt-Cike-БТ. (И） Затем подставим tz = 0ty-b в уравнение (10)и подставим t = 0, j ^ = 0 в уравнение(11), чтобы получить систему уравнений. 0 =С3А—САЛ、

Откуда? В конце： х = * * * \ \ Т%(5） Иначе говоря Г = [б -^) ч * Ф + *. (12） Итак, уравнение движения для точки массы принимает вид: Да. к. г = [Б -£) chkt + $. (12） Чтобы определить уравнение орбиты точки, необходимо исключить время из уравнения движения. Из (5) и(12) можно увидеть следующее: Да, сэр. ш КТ= -, в г-к г к-ч КТ =-. учитывая, что clrVef-sh * / s? = 0, ф = v0r = вентиляционно-перфузионное грех, 9o = ^ потому что. Действительно, если указать начальное значение 0 = ^ Cosa. К снаряду прилагается только сила

притяжения F ’. Котенок. Расстояние до центра Земли пропорционально мощности 2.То есть,/ 7 =-. На поверхности Земли, то есть, если Р = Р, Ф = Р = tngt, мы находим, что K = гри. Так… Ф.^ (2） Сила притяжения F направлена к центру О. Вид дифференциального уравнения для движения точки масс в проекции на ось полярной координаты имеет следующий вид: В этом деле Фр = — Ф= -^, ФВ = 0 Следовательно： (3） =(4） Из дифференциального уравнения (4) следует Интеграл площади:?? = C, то есть rQ =: Rt, и если есть выражение (1), Запишите выражение (5) в следующем виде: Р * < Дж>

= Rv0 потому что、 Откуда? ^ = / ?v0cosa(б） (g * ^® — производная по времени от площади, описываемой в 2 раза секторной скоростью снаряда, то есть радиус-вектором снаряда R. So, в Центральном движении точки масс ее секторная скорость постоянна. Рассмотрим Интеграл дифференциального уравнения (3).Используя формулу(6), запишите это уравнение в виде: cos3 р а_ Умножьте термины на dr, чтобы интегрировать их. ？д-р = д±д-р = ТДТ. Так… Что купить： G *, P’G COS3 a_f r 2 ’г’ Поскольку в начальном положении снаряда r = r0=#, r-

prG0F0 = z / 0 sin a, интегральная постоянная принимает вид: Р 2г /?- pjj 2 Так… ф8, потому что * * 2 ^ /? — Ф ^ М 2 ′ 2r2-T 2• Формула (7) устанавливает зависимость между проекцией скорости снаряда f на ось g и радиус-вектором g. В высшей точке траектории проекция скорости снаряда на ось Z равна нулю. То есть, если r = rmx / =-0.Подставьте эти значения в формулу (7), чтобы получить уравнение rm2X 2-го порядка. (2gR-в*) Т * Макс-2gR? Р, Макс + Rtfcos * а = 0、 Откуда? Р-^^ cos2 а、 Гшах-2гр ^ — в-т к- {*） Из Формулы (8) следует, что если vl = < logR, то значение rmax бесконечно. То есть оболочка не возвращается на Землю(v0 =] / r2gR = 11,2 км / с называется 2-й космической скоростью).Таким образом, снаряд должен быть информирован о начальной скорости, то есть v0 0. ■р ^ О.

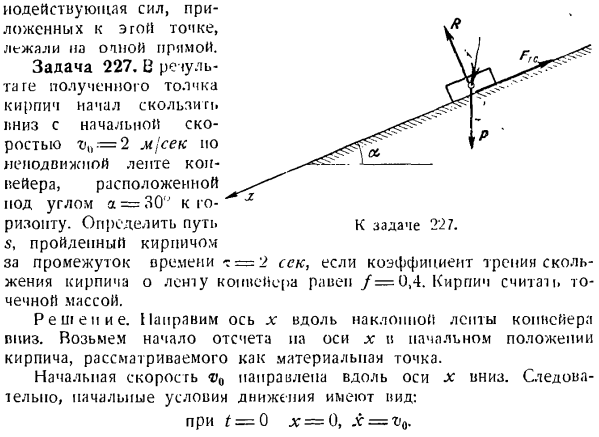
Актерское мастерство! Единая сила, приложенная к точкам эго, лежала в полной временной линии. Проблема 227.As в результате работы движителя кирпич начал сползать вниз с начальной скоростью tv = 2 Mjcetc, вдоль неподвижного конвейерного долота в положении угла a = 30 относительно горизонта. Задача 227. Определите путь до 5. Если коэффициент трения скольжения кирпича по конвейерной ленте равен/ = 0,4, то за определенный период^ =

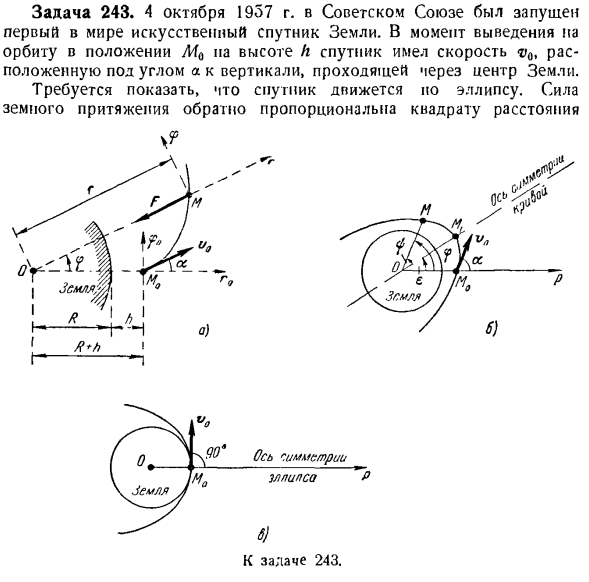
2 секунды. Кирпичи считаются «точечной массой». Решение. Точки оси X вдоль наклонной конвейерной ленты. Принимает по оси X начало координат начального положения кирпича, которое считается точкой масс. Начальная скорость φ0-это папла плена вниз вдоль x-axis. So, начальными условиями для управления средствами являются: если t = 0 x-0, то x = vQ. Максимальная высота полета снаряда на поверхности Земли N = Gt * x-R- Используя формулу(8), получаем следующее: Если вы отбросите отрицательное значение Ht, вы в конечном итоге обнаружите, что: Ч-ВГР-ви Если начальная скорость направлена вертикально зет. до, то есть =： _ fivj н-2 гр-вый Задача 243.1957/10/4 первый в мире искусственный спутник Земли был запущен в Советском Союзе. При орбите положения MQ на высоте

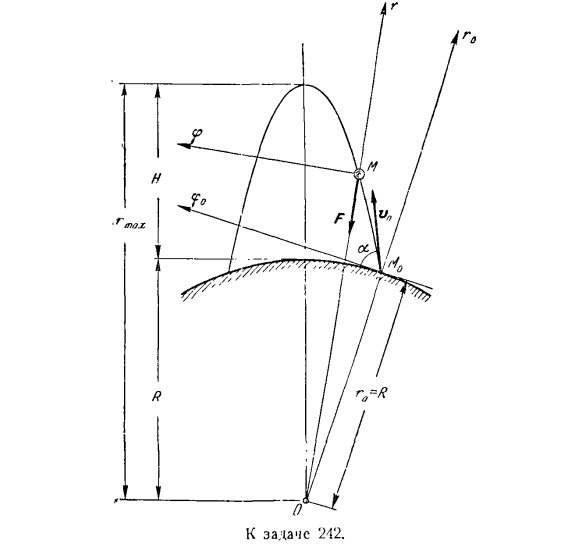
h спутник имел скорость vQt, расположенную под углом a к вертикальной линии, проходящей через центр Земли. Следует отметить, что спутник движется в направлении овала. Гравитация обратно пропорциональна квадрату расстояния 5? Земля.;- Спутник из центра Земли. Гравитационное ускорение земной поверхности равно g. радиус Земли R. игнорируйте сопротивление движению. Решение. Поскольку начальная скорость vQ и сила тяжести F находятся в одной плоскости, орбита спутника является плоской curve. So, выберем полярную систему координат с полюсами O

в центре Земли(рис. Радиуса-вектора ом, подключается к средней позиции, м, со спутника перемещение полюса. Вдоль оси OM нарисуйте ось z и выпейте вертикально через точку M-ось 9.М0-начальное положение спутника на орбите. Из рассматриваемого состояния начальным состоянием движения спутника является: Для 1 = 0 r = r0 = R + h, 9 = 0、 р = = «п / ^ О = ^и с°ы = в / грех、 Это объясняется тем, что при представлении начального значения φ в φο, npfot> 0 = r0

Из Дифференциального Уравнения(5)： ГХ =С. (6） Так как секторная скорость точки, то есть производная по времени от площади S, описываемой вектором радиуса r, равна$ =、 Именно поэтому секторная скорость спутника постоянна, то есть r’, φ= r2r0.Используя формулу(1), Запишите формулу (b)в виде: С = r2ph0 = r0z / 0sin в、 Откуда? Т =(7） Приступим к изучению

дифференциальных уравнений(4）： вычислите производную по времени от g. учитывая G =выражение(7), она выглядит следующим образом: доктор rQvQ грех Д {1 \ / АВ Ф = D4 л»: = — грех * д,(р) «(8） «Как мне взломать?»=^=Далее, используя формулы(7)и (8), получаем: Запишите дифференциальные уравнения (7) и (9) с учетом (4).И затем… Пн * грех г-диджей(1 \ РФО * sinea ФФГ Р2 риф?3 \ г J и РЖ ~~ Р-• д. Куда? l-ZR2 Рив * Sin5 в * Интегрируем дифференциальное

уравнение(10) для определения искомого уравнения орбиты спутника в полярных координатах. (Дифференциальное уравнение(10) может быть получено непосредственно с помощью уравнения Biie. д <?\ r) ’r -’ tC * ’C-двойная секторная скорость: C = 2″ S = r0vQ sin a, a Уравнение(10) является неоднородным линейным дифференциальным уравнением для постоянных коэффициентов. Его Общее решение равно сумме общего решения Однородное уравнение у + б» <«» И тогда некоторое решение неоднородного уравнения j, т. е. 7 = + 04 Для решения дифференциального уравнения (11) создайте

характеристическое уравнение X9 −1 == 0.Где X = itL Spedovatelio、 (г), Б= в COS(<?- е), (13） Где B и e — константы интегрирования, которые будут определены позже. Нетрудно заметить, что удельное решение дифференциального уравнения(10) равно постоянной правой части. (} \ = L. (14） Используйте формулы (13) и (14) для описания общего решения по формуле (12).Форма Я = б в COS(<Р-Е)С-л.(15） Уравнение эго-это орбитальное уравнение спутника. Чтобы определить константы интегрирования B и e, используйте pro-I Время от времени я： — ПФ == — я <B грех (ин-е). (16）

Присвоить уравнению (15) r = r0 = A> + K? =Р = р = РК = Р + кв <р = 0, р = ри = качеству звука потому что, из Формулы (ИД). ва грех в< грех » ФО== Фо=: — ~~- Р + Л ’ Получаем систему уравнений. (П） грех-р + ч по качеству звука потому что  ж + ч? — Син е. Чтобы определить интегральные константы B и e из уравнения (17), запишите эту систему в виде: в COS е = 1.- — А.、 (18) (19） Р + ч Из системы (18) и (19) найдите следующее: или, после простого преобразования, замените значение A. * = «+V 1—(R-GA)) (20） Разделите (19)на (18), чтобы найти

tan e、 — ДГС1Г + Sin ot Cosa + sin2a ’ Вернемся к уравнению орбиты спутника, записанному в виде (15). если мы решим это уравнение относительно r, то увидим, что: 1_ а и cos(<р-е） Или Г = » Я + Е, потому что е» Куда? ’- (Подоконник ЖВ бы П-А〜 ’ ГК * ’ «- J = / +(24） И Ф =? (Л> 5） Вес кирпича выражается в R. To к кирпичу, являющемуся точкой несвободного материала, прилагается сила одного набора-то есть собака Р. применяет принцип освобождения от скрепления, мысленно отбрасывает косую ленту конвейера и заменяет действие

на кирпич соответствующей реактивной силой. В этой реактивной силе есть 2 элемента. Обычными элементами являются сила реакции FT перпендикулярная плоскости клещей и сила трения скольжения Fr от кирпича к конвейеру belt. It направляется вверх в противоположном направлении от движения, то есть вдоль конвейерной ленты. Напишите дифференциальное уравнение движения массовой точки, проецируемой на ось l’. н. МХ =£Фукса. к-мне В данном случае это выглядит так: > — да. V = Р ЗША-фут ов. (Г Т ’

Потому что, согласно закону сухого трения, FTtC = fN = / P cosa после уменьшения PanaP、 Джей?= Р£(сни а — / соз а). (1） Чтобы интегрировать дифференциальное уравнение движения, замените L1 pa. После разделения переменных, вы получите следующее: с интеграцией dx = g (sin a ~ / cos a) dt вы можете: ДжейТи-г(грех а — / соз а)/ — П-С,. (2） Где E-выражение (2!Он определяется по названию компании). Как известно из курса аналитической геометрии, уравнение (22)является уравнением кривой 2-го порядка в Полярном coordinates. In IT, p-параметр кривой, а e-эксцентриситет. Кривая

выглядит следующим образом: а) круг£= 0. Б) Эллипс в) парабола e = \d) гиперболический угол φ t> 1 измеряется от оси симметрии Кривой до радиуса искателя. Радиусный Искатель определяет положение точки M на кривой (см. Рисунок Tf), а ось симметрии направлена от 1 полюса O (в данном случае центра Земли) в фокусную точку кривой. К пику, ближайшему к фокусу. Угол е определяет положение оси симметрии кривой. Рассмотрим характер начальных условий запуска спутников, чтобы они могли двигаться вдоль каждой из этих

кривых. а) для того чтобы спутник двигался по кругу, он должен удовлетворять условию ξ= 0.То есть по формуле (24)、 Г + о. Здесь мы получаем Би-квадратное уравнение для начальной скорости г / 0 спутника на орбите. (Р + Ш вентиляционно-перфузионное грех * а-(р + ч) в] грех * А + Г * Р * = 0、 Y Иначе говоря Комплексные значения указывают на то, что движение спутника по круговой орбите возможно только в определенных случаях, то есть в горизонтальном направлении от начальной скорости vQ. И затем… (26） / <> + ч ’ (Эта формула взята в выпуске 220 выше.） 6) чтобы спутник двигался

по эллипсу, должно быть выполнено условие. То есть по формуле (24)、 / 1 _ ш + [зду-(я+»), я | <1. Чтобы достичь этого неравенства, нам нужно: 2″? — ( / ?+ * ) * {>0、 Иначе говоря г.— Поэтому для того, чтобы спутник двигался по эллипсоиду, начальная скорость на орбите v0 должна соответствовать условиям (27） Однако этого условия

недостаточно, так как эллиптическая орбита спутника не проходит внутри Земли. Поэтому минимальное расстояние r должно быть больше или равно радиусу R Земли. (28） Расстояние от фокусной точки O в сочетании с центром Земли до точки на эллипсе является самым коротким в момент, когда спутник проходит через позицию M(см. Рисунок B).То есть, если<|> = 0.Таким образом, находим значение r из уравнения неравенства (28) (22), предполагая, что φ= 0、 Из формул (23) и (24), подставляя значения p и e в неравенство (29), находим результат ряда преобразований. 3 = в ^ ОТО ^ Р-ЭБ /—р-х

И Л ви-(30） Если мы сравним неравенства (27)и (30), то увидим, что условия, при которых спутник движется вокруг Земли по эллиптической орбите, можно описать в следующем виде: Где U-начальная скорость спутника на орбите. h-высота первого спутника на поверхности Земли. g-ускорение силы тяжести на поверхности Земли. И-угол, образованный начальной скоростью с вертикальной линией. Для того, чтобы левая часть неравенства (31) стала реальностью、 Р. Грех. Р + ч ’ Во время запуска спутника от поверхности Земли, то есть когда= 0, зта | = 1, то есть А = Г И; и = г(см. рис. c).Однако в этом случае левая часть неравенства (31) является неформатированной. sin a] = 1, затем укажите h на пулю, и мы получим неравенство VgR ^ v0 <VlgR-(32）

£ = 9,81 м / с *и/? = 6370 км, имеем: 7,9 км j сек^ vQ 11,2 км /сек. Так, при запуске спутника с поверхности земли для перемещения по эллиптической орбите модуль его начальной скорости должен удовлетворять неравенствам (33), а начальная скорость должна быть направлена горизонтально. Значение v = 7,9 км / с называется первой космической скоростью, а значение v = 11,2 км / с-второй космической скоростью. v0 <[7,9 км] секунды, объект упадет на Землю. в) чтобы объект двигался по параболе, должно быть выполнено условие e=].Из Формулы (24), Если e = 1 2gR *- (R + h) vl = 0 г)Для того чтобы тело двигалось по гиперболе, должны быть выполнены следующие условия: Из формул (34)и (35)、 О） Тело движется по параболе или гиперболе. То есть, спутник Земли снимается не endlessly. In кроме того, в первый момент, если объект находится на поверхности Земли, то есть/ / = 0, то из Формулы (36):： Коммер-Санту&Уш(37） Иначе говоря 11,2 км / с (38 км）

Смотрите также:

Предмет теоретическая механика

Основные формы дифференциальных уравнений динамики материальной точки	Колебательное движение
Определение сил по заданному движению	Относительное движение