Определение достаточной статистики, теорема факторизации

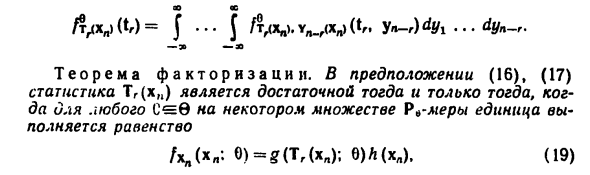
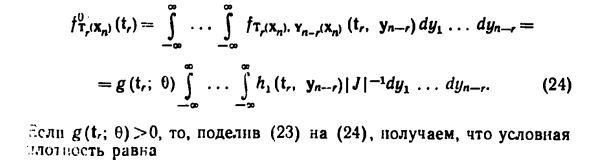
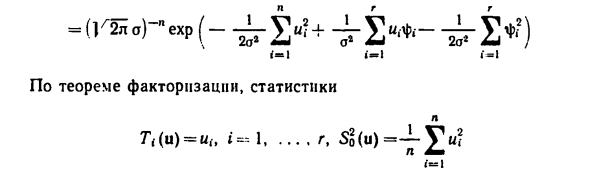
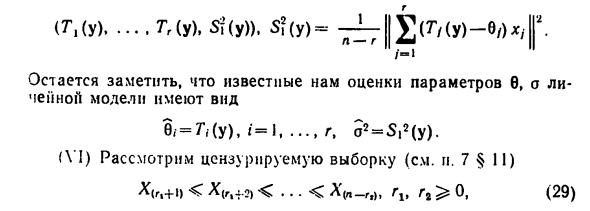
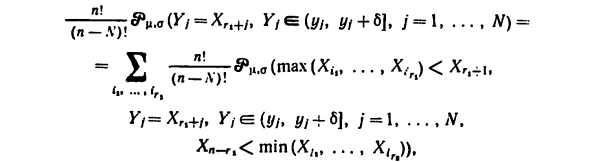
Определение достаточной статистики, теорема факторизации

• Как уже упоминалось, достаточной статистической концепцией является Непрерывная модель полностью аналогична дискретному случаю. один Однако математическая очевидность связана с условным введением Вероятностный, не дает хорошего определения Статистика общего формата. PA- Параметрические модели, и если не указано иное Такая статистика Tr (xn) = Gi (xn), …, 7r (xn)) 139 Статистика Инн. (Xn) = (Y \ (xn) Y ,, -, (xn)) Подстановка переменных u = Tx (kn) tr = Tr (xn), yi в Yi (xn), …, yn-r = Yn-r (xn) A6) Один на один для любого из наборов переоценки 0e0, и плотность меры Po в координатах x „и (t ,, y ,, _ r) связаны между собой Один из наборов переоценки — это отношения Yn.r (xn) (tr, yn-r) \ J \, A7) тр. Ух ты г) где т, …, хр)

Якобиан перехода от координат (tr, yn-r) к (x „). То есть предположения А6) и А7) Во-первых, есть случайные плотности векторов (Tr (Xn), Yn-r (Xn)), Затем при расчете с использованием этой плотности интеграл I ••• J / Wv, cxn) (tr, Yn-r) A, … dt4yl ¦. ¦ dyn-r в Вы можете уменьшить это с помощью изменения переменной A6) Следующая необходимая в Где B — обратное к B под картой A6. Предположим, что статистика определения Tj (xn) имеет следующий вид: Допущения А6) и А7) были выполнены. Когда определяется условная плотность U и 8 определены. / м (хп) (М> 0. HW

Если вы полагаетесь на 8e8, статистика Tj (xn) называется достаточно Для этой модели. Людмила Фирмаль

Пожалуйста, обратите внимание se ac / Yxn) (т,) = J … {/ т ^ V-WW ^. y ^ r) dy1 … dyn-r. -3D-М Теорема факторизации. А6), А7) предполагается Статистический Tr (xn) достаточен, только если: В случае Оля с 0 = 9 в наборе Pv-меры, единица равна Равенство / x „(x„: 0) = g (T, (x ,,); 6) th (chl), A9) 140 Где g (. \ Fl) и A (xn) неотрицательные измеримые функции H (x ,,) для каждого из аргументов µ и x не зависит от 8. Доказательство. Предположим, что статистика T (xn) достаточна. по Put L для каждой пары (tr, yn-r), где существует 8e9 frr (Xn) {tr)> 0, положить r | t,). B0) Учитывая достаточность статистики T (xn), функция / ii (t ,, yn_,)

Уравнение B0 правильно определено (функция tr, Yn-r) и уравнение B0), каждые 6 тр, справа Детали определяются и выполняются в заданной P «-измерительной единице. Получите равенство от A8), с учетом введенной записи т. Cn-r), B1) Единицы, откуда использовать действительные для набора мер P0 А7), получить / xn (xn> =? (Tlxn); ejA ^ T ^ x,), Yy ^ (xy)) | Y |. B2) Множество A = Ai независимо от якобиана | / | 8 независимых | / | Получите выражение A9). И наоборот, продолжите разложение A9).

• Определения Функция A | (t ,, y ,, — ,,) условие li (x ,,) = h, {tr, y „-r), t, = T, (xn), yn-r = Yn_r (xn) Перейти к A9), перейти к координатам (tr, y „_r) и все Выполните аргумент с подмножеством 95, где Λ |> 0, Λ> 0. Перепишите, используя формулу преобразования A7) A9), как r Yn.r (xn, (t, .yn-r) \ J \ = g {t ;; 9) h, (tnyn-r). B3) Найдите статистическую плотность TG (X „) отсюда. tg (xy) (tr) = J • .. J / y „>. y„. ^ xy) (тр. = g (t, J0) J … j A, a, yn-r) \ J \ -ldyi … dyn-r. B4) D. Если g (\, \ 8)> 0, то разделить B3) на B4), чтобы получить условное выражение «Росио равен JI-l / J … Если K (tr, zn-r) IJI — * — к Кроме того, это не зависит от 6, которые должны были быть установлены.

да Например, нарисуйте случайную плотность образца из нормы Нормальное распределение N вида ([x, а) B5> л л Оказывается, пары (V x (, Y] a; I достаточно). (= 1 (= я Цтной указан непосредственно выше (см. А5). Теорема факторизации вида примера (I) Условное распределение выборки Достаточный статистический ряд вариаций условий Это является дискретным. Это один из редких случаев в приложении. Предварительные условия A6) и A7) не выполнены.

Достаточность того, что рассматривается в примерах (II) — (IV) Статистика с использованием теоремы факторизации полностью установлена Простой. Людмила Фирмаль

Obura Давайте посмотрим на другой пример. (V) Рассмотрим линейную статистическую модель с нормалями Нормальные наблюдения в стандартной форме (см. G) §10): Ui = ^ i + a6i, i = lr; (L = od /, i = r + 1l, B6) Где ^ = (\ fi. ••• .φ). o> 0 с неизвестными параметрами, Fi, 62, … ••• »bp) -стандартный нормальный вектор. Плотность распределения U распределения равны И? ) = Я (= 1 i = l 1 = 1 По теореме факторизации статистика L 7, (u) = u, -, i-1, …, r, So (u) = -Ltii ПК шт Сформируйте достаточную статистику в измерениях r + 1. Эквивалент Ее статистика L G \ (u) r, (u), 5? (U)), 5? (U) = — ^ — V а] Но достаточно. Оценки> j), = 7, (u), o2 = В §10 была введена линейная модель ip-параметра 5r (u).

Ситуация такая же, как и для нормальной линейной модели. Общая форма A) Матрица полного ранга X из § 13. плотность Распределение наблюдений в этом случае .-1 , C = @ 1, …, 6G), B7) X = [x1, …, x’r], x / = (n; 1 //, … xy), / = 1, …. Введите статистику 7 «, — (y), / = 1g в качестве коэффициента расширения Проекции вектора y в подпространство V, порожденное Вектор x ,, f = 1, …, r … + Tg (y) xi. вектор Далее, используя теорему Пифагора, l | y — eJC ‘| la = ll (Y— »pvy + n ^ -y — bX’) ||« = || y — pr „y ||« + || prouu — bX ‘| T И ^ II II * -II Подставляя B8) в B7), применяя теорему факторизации, Получите достаточно статистики в форме , (Y). •••• Tg (y), | Оценки параметров Формат модели цепочки 8, = 7 \ (у), а = 1 г, а2 = 5,2 (у). (\ 1) пересмотреть цензурированные образцы (см. Раздел 7 §11) X (ri + i, 0, B9) 143

Наблюдение Xi …. N (n, a) -распределено- независимо от Xn а) -распределенная и Г \, м-2. -Фиксированный номер. Найти плотность Распределение вектора Y = [Ylt …. Vv) — (X (,, Ri), X (, 1 + 2), …. X (R-r ^), N — n — r, -r ,, В точке y = (yx y) y \ [Выполнить формальный расчет. б> 0 так ма Интервал (yit t // + 6), i = 1, …, W не пересекаются, Мы пишем ^ m> 0 (K / e («//, y, + b],; = 1 LO = +? # V.o (> ‘/ -Xft /, К / € = (у /, Л + б],} + 1АГ) C1) Где сумма является порядком всех n (n-1) … (n-, V + 1). Набор заказанных индексов (кит кб …. кн) Установите 1, 2, …. п. Сумма всех добавлений С1) Если они равны, перепишите в виде С1) T ^ ZW ^ 11 (Макс (Си X / J Yl = Xrt + h Y, t = (yh y, +6] ;; = 1 N Xw, <мин (X; Xlrt)), Где сумма неупорядочена для всех CJ_ ^.

Набор показателей iv t2, …. tV, без повторов из набора {1, …, T |, n-r2 + 1, … n}, a / lt / 2, •••. R — оставшийся элемент Элементы этого набора. Опять общее добавление С2) Если они равны друг другу, получим выражение С2) C,? . V меня! ^ „. A (max (Xx X„) . <Мин (* ,, _. + *„)). C3j Напишите очевидную верхнюю оценку для C3): -2C ^ m.a (max (X1 (…. Xg.) 0, G2> 0) Н х Если цензура односторонняя: если rt = 0 или r2 = 0, y \ или y, \ Поэтому достаточно статистики, которую нужно отбросить Оказалось трехмерным.

Смотрите также:

• Примеры решения задач по статистике

Подобные статистики	Экспоненциальные семейства, минимальная достаточность
Достаточные статистики в дискретной модели	Полные достаточные статистики

Если вам потребуется помощь по статистике вы всегда можете написать мне в whatsapp.